radial Mathieu functions

SearchAdvancedHelp

(0.005 seconds)

1—10 of 15 matching pages

1: 28.20 Definitions and Basic Properties

… ►

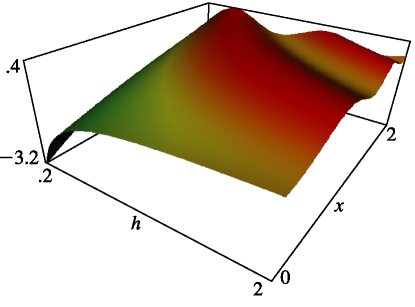
§28.20(iv) Radial Mathieu Functions ${\mathrm{Mc}}_n^{(j)}$, ${\mathrm{Ms}}_n^{(j)}$

… ►

28.20.15 $${\mathrm{Mc}}_n^{(j)}(z,h)={\mathrm{M}}_n^{(j)}(z,h),$$ $n=0,1,\mathrm{\dots }$,

ⓘ

Defines:

${\mathrm{Mc}}_n^{(j)}(z,h)$: radial Mathieu function

Symbols:

${\mathrm{M}}_{\nu }^{(j)}(z,h)$: modified Mathieu function, $h$: parameter, $n$: integer, $j$: integer and $z$: complex variable

Referenced by:

§28.20(vii)

Permalink:

http://dlmf.nist.gov/28.20.E15

Encodings:

pMML, png, TeX

See also:

Annotations for §28.20(iv), §28.20 and Ch.28

►

28.20.16 $${\mathrm{Ms}}_n^{(j)}(z,h)={(-1)}^n{\mathrm{M}}_{-n}^{(j)}(z,h),$$ $n=1,2,\mathrm{\dots }$.

ⓘ

Defines:

${\mathrm{Ms}}_n^{(j)}(z,h)$: radial Mathieu function

Symbols:

${\mathrm{M}}_{\nu }^{(j)}(z,h)$: modified Mathieu function, $h$: parameter, $n$: integer, $j$: integer and $z$: complex variable

Referenced by:

§28.20(vii)

Permalink:

http://dlmf.nist.gov/28.20.E16

Encodings:

pMML, png, TeX

See also:

Annotations for §28.20(iv), §28.20 and Ch.28

… ►

28.20.17 $${\mathrm{Ie}}_n(z,h)={\mathrm{i}}^{-n}{\mathrm{Mc}}_n^{(1)}(z,\mathrm{i}h),$$

ⓘ

Defines:

${\mathrm{Ie}}_n(z,h)$: modified Mathieu function

Symbols:

$\mathrm{i}$: imaginary unit, ${\mathrm{Mc}}_n^{(j)}(z,h)$: radial Mathieu function, $h$: parameter, $n$: integer and $z$: complex variable

A&S Ref:

20.8.10 (in slightly different form)

Permalink:

http://dlmf.nist.gov/28.20.E17

Encodings:

pMML, png, TeX

See also:

Annotations for §28.20(v), §28.20 and Ch.28

… ►

§28.20(vii) Shift of Variable

…

2: 28.21 Graphics

… ►

Radial Mathieu Functions: Surfaces

… ►

►

►

Figure 28.21.6: ${\mathrm{Ms}}_1^{(2)}(x,h)$ for $0.2\le h\le 2$, $0\le x\le 2$. Magnify 3D Help

3: 28.22 Connection Formulas

… ►

28.22.1 $${\mathrm{Mc}}_m^{(1)}(z,h)=\sqrt{\frac{2}{\pi }}\frac{1}{g_{e,m}(h){\mathrm{ce}}_m(0,h^2)}{\mathrm{Ce}}_m(z,h^2),$$

ⓘ

Symbols:

${\mathrm{ce}}_n(z,q)$: Mathieu function, $\pi$: the ratio of the circumference of a circle to its diameter, ${\mathrm{Ce}}_{\nu }(z,q)$: modified Mathieu function, ${\mathrm{Mc}}_n^{(j)}(z,h)$: radial Mathieu function, $m$: integer, $h$: parameter, $z$: complex variable and $g_{e,n}(h)$, $g_{o,n}(h)$: joining factors

A&S Ref:

20.6.15 (in different form)

Permalink:

http://dlmf.nist.gov/28.22.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §28.22(i), §28.22 and Ch.28

►

28.22.2 $${\mathrm{Ms}}_m^{(1)}(z,h)=\sqrt{\frac{2}{\pi }}\frac{1}{g_{o,m}(h){\mathrm{se}}_m^{\prime }(0,h^2)}{\mathrm{Se}}_m(z,h^2),$$

ⓘ

Symbols:

${\mathrm{se}}_n(z,q)$: Mathieu function, $\pi$: the ratio of the circumference of a circle to its diameter, ${\mathrm{Ms}}_n^{(j)}(z,h)$: radial Mathieu function, ${\mathrm{Se}}_{\nu }(z,q)$: modified Mathieu function, $m$: integer, $h$: parameter, $z$: complex variable and $g_{e,n}(h)$, $g_{o,n}(h)$: joining factors

Permalink:

http://dlmf.nist.gov/28.22.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §28.22(i), §28.22 and Ch.28

… ►The joining factors in the above formulas are given by … ►

28.22.9 $$f_{e,m}(h)=-\sqrt{\pi /2}{g}_{e,m}(h){\mathrm{Mc}}_m^{(2)}(0,h),$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, ${\mathrm{Mc}}_n^{(j)}(z,h)$: radial Mathieu function, $m$: integer, $h$: parameter, $g_{e,n}(h)$, $g_{o,n}(h)$: joining factors and $f_{e,n}(h)$, $f_{o,n}(h)$: joining factors

A&S Ref:

20.8.12 (in slightly different form)

Permalink:

http://dlmf.nist.gov/28.22.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §28.22(i), §28.22 and Ch.28

… ►

$${\mathrm{ge}}_m(0,h^2)=\frac{1}{2}\pi S_m(h^2){\left(g_{o,m}(h)\right)}^2{\mathrm{se}}_m^{\prime }(0,h^2).$$

…

4: 28.23 Expansions in Series of Bessel Functions

§28.23 Expansions in Series of Bessel Functions

… ►

28.23.6 $${\mathrm{Mc}}_{2m}^{(j)}(z,h)={(-1)}^m{\left({\mathrm{ce}}_{2m}(0,h^2)\right)}^{-1}\sum _{\mathrm{\ell }=0}^{\mathrm{\infty }}{(-1)}^{\mathrm{\ell }}{A}_{2\mathrm{\ell }}^{2m}(h^2){𝒞}_{2\mathrm{\ell }}^{(j)}(2h\cosh z),$$

ⓘ

Symbols:

${\mathrm{ce}}_n(z,q)$: Mathieu function, $\cosh z$: hyperbolic cosine function, ${\mathrm{Mc}}_n^{(j)}(z,h)$: radial Mathieu function, $m$: integer, $h$: parameter, $j$: integer, $z$: complex variable, ${𝒞}_{\mu }^{(j)}$: cylinder functions and $A_m(q)$: Fourier coefficient

A&S Ref:

20.6.12

Referenced by:

§28.23

Permalink:

http://dlmf.nist.gov/28.23.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §28.23 and Ch.28

►

28.23.7 $${\mathrm{Mc}}_{2m}^{(j)}(z,h)={(-1)}^m{\left({\mathrm{ce}}_{2m}(\frac{1}{2}\pi ,h^2)\right)}^{-1}\sum _{\mathrm{\ell }=0}^{\mathrm{\infty }}{A}_{2\mathrm{\ell }}^{2m}(h^2){𝒞}_{2\mathrm{\ell }}^{(j)}(2h\sinh z),$$

ⓘ

Symbols:

${\mathrm{ce}}_n(z,q)$: Mathieu function, $\pi$: the ratio of the circumference of a circle to its diameter, $\sinh z$: hyperbolic sine function, ${\mathrm{Mc}}_n^{(j)}(z,h)$: radial Mathieu function, $m$: integer, $h$: parameter, $j$: integer, $z$: complex variable, ${𝒞}_{\mu }^{(j)}$: cylinder functions and $A_m(q)$: Fourier coefficient

Permalink:

http://dlmf.nist.gov/28.23.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §28.23 and Ch.28

►

28.23.8 $${\mathrm{Mc}}_{2m+1}^{(j)}(z,h)={(-1)}^m{\left({\mathrm{ce}}_{2m+1}(0,h^2)\right)}^{-1}\sum _{\mathrm{\ell }=0}^{\mathrm{\infty }}{(-1)}^{\mathrm{\ell }}{A}_{2\mathrm{\ell }+1}^{2m+1}(h^2){𝒞}_{2\mathrm{\ell }+1}^{(j)}(2h\cosh z),$$

ⓘ

Symbols:

${\mathrm{ce}}_n(z,q)$: Mathieu function, $\cosh z$: hyperbolic cosine function, ${\mathrm{Mc}}_n^{(j)}(z,h)$: radial Mathieu function, $m$: integer, $h$: parameter, $j$: integer, $z$: complex variable, ${𝒞}_{\mu }^{(j)}$: cylinder functions and $A_m(q)$: Fourier coefficient

Permalink:

http://dlmf.nist.gov/28.23.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §28.23 and Ch.28

… ►

5: 28.28 Integrals, Integral Representations, and Integral Equations

… ►

§28.28(i) Equations with Elementary Kernels

… ►

28.28.23 $$\frac{2}{\pi }{\int }_0^{\pi }{𝒞}_{2\mathrm{\ell }+2}^{(j)}(2hR)\sin \left((2\mathrm{\ell }+2)\varphi \right){\mathrm{se}}_{2m+2}(t,h^2)dt={(-1)}^{\mathrm{\ell }+m}{B}_{2\mathrm{\ell }+2}^{2m+2}(h^2){\mathrm{Ms}}_{2m+2}^{(j)}(z,h).$$

ⓘ

Symbols:

${\mathrm{se}}_n(z,q)$: Mathieu function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\int$: integral, ${\mathrm{Ms}}_n^{(j)}(z,h)$: radial Mathieu function, $\sin z$: sine function, $m$: integer, $h$: parameter, $j$: integer, $z$: complex variable, ${𝒞}_{\mu }^{(j)}$: cylinder functions, $\varphi (z,t)$: function, $R(z,t)$: function and $B_m(q)$: Fourier coefficient

A&S Ref:

20.7.28 (in different form and only for $\mathrm{\ell }=0$)

Permalink:

http://dlmf.nist.gov/28.28.E23

Encodings:

pMML, png, TeX

See also:

Annotations for §28.28(ii), §28.28 and Ch.28

… ►

§28.28(iv) Integrals of Products of Mathieu Functions of Integer Order

… ►

28.28.49 $${\widehat{\alpha }}_{n,m}^{(c)}=\frac{1}{2\pi }{\int }_0^{2\pi }\cos t{\mathrm{ce}}_n(t,h^2){\mathrm{ce}}_m(t,h^2)dt={(-1)}^{p+1}\frac{2}{\mathrm{i}\pi }\frac{{\mathrm{ce}}_n(0,h^2){\mathrm{ce}}_m(0,h^2)}{h{\mathrm{Dc}}_0(n,m,0)}.$$

ⓘ

Defines:

${\widehat{\alpha }}_{n,m}$ (locally)

Symbols:

${\mathrm{Dc}}_j(n,m,z)$: cross-products of radial Mathieu functions and their derivatives, ${\mathrm{ce}}_n(z,q)$: Mathieu function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $dx$: differential of $x$ , $\mathrm{i}$: imaginary unit, $\int$: integral, $m$: integer, $h$: parameter and $n$: integer

Permalink:

http://dlmf.nist.gov/28.28.E49

Encodings:

pMML, png, TeX

See also:

Annotations for §28.28(iv), §28.28 and Ch.28

►

§28.28(v) Compendia

…

6: 28.1 Special Notation

… ► ►►

${\mathrm{Ce}}_{\nu }(z,q)$,	${\mathrm{Se}}_{\nu }(z,q)$,	${\mathrm{Fe}}_n(z,q)$,	${\mathrm{Ge}}_n(z,q)$,
…

►The functions ${\mathrm{Mc}}_n^{(j)}(z,h)$ and ${\mathrm{Ms}}_n^{(j)}(z,h)$ are also known as the radial Mathieu functions. … ►

$f_{o,n}(h).$

… ►The radial functions ${\mathrm{Mc}}_n^{(j)}(z,h)$ and ${\mathrm{Ms}}_n^{(j)}(z,h)$ are denoted by ${\mathrm{Mc}}_n^{(j)}(z,q)$ and ${\mathrm{Ms}}_n^{(j)}(z,q)$, respectively.

7: 28.24 Expansions in Series of Cross-Products of Bessel Functions or Modified Bessel Functions

§28.24 Expansions in Series of Cross-Products of Bessel Functions or Modified Bessel Functions

… ►

28.24.2 $${\epsilon }_s{\mathrm{Mc}}_{2m}^{(j)}(z,h)={(-1)}^m\sum _{\mathrm{\ell }=0}^{\mathrm{\infty }}{(-1)}^{\mathrm{\ell }}\frac{A_{2\mathrm{\ell }}^{2m}(h^2)}{A_{2s}^{2m}(h^2)}\left(J_{\mathrm{\ell }-s}\left(h{\mathrm{e}}^{-z}\right){𝒞}_{\mathrm{\ell }+s}^{(j)}(h{\mathrm{e}}^z)+J_{\mathrm{\ell }+s}\left(h{\mathrm{e}}^{-z}\right){𝒞}_{\mathrm{\ell }-s}^{(j)}(h{\mathrm{e}}^z)\right),$$

ⓘ

Symbols:

$J_{\nu }\left(z\right)$: Bessel function of the first kind, $\mathrm{e}$: base of natural logarithm, ${\mathrm{Mc}}_n^{(j)}(z,h)$: radial Mathieu function, $m$: integer, $h$: parameter, $j$: integer, $z$: complex variable, ${𝒞}_{\mu }^{(j)}$: cylinder functions, ${\epsilon }_s$: constants and $A_m(q)$: Fourier coefficient

A&S Ref:

20.6.7

Permalink:

http://dlmf.nist.gov/28.24.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §28.24 and Ch.28

►

28.24.3 $${\mathrm{Mc}}_{2m+1}^{(j)}(z,h)={(-1)}^m\sum _{\mathrm{\ell }=0}^{\mathrm{\infty }}{(-1)}^{\mathrm{\ell }}\frac{A_{2\mathrm{\ell }+1}^{2m+1}(h^2)}{A_{2s+1}^{2m+1}(h^2)}\left(J_{\mathrm{\ell }-s}\left(h{\mathrm{e}}^{-z}\right){𝒞}_{\mathrm{\ell }+s+1}^{(j)}(h{\mathrm{e}}^z)+J_{\mathrm{\ell }+s+1}\left(h{\mathrm{e}}^{-z}\right){𝒞}_{\mathrm{\ell }-s}^{(j)}(h{\mathrm{e}}^z)\right),$$

ⓘ

Symbols:

$J_{\nu }\left(z\right)$: Bessel function of the first kind, $\mathrm{e}$: base of natural logarithm, ${\mathrm{Mc}}_n^{(j)}(z,h)$: radial Mathieu function, $m$: integer, $h$: parameter, $j$: integer, $z$: complex variable, ${𝒞}_{\mu }^{(j)}$: cylinder functions and $A_m(q)$: Fourier coefficient

A&S Ref:

20.6.8

Permalink:

http://dlmf.nist.gov/28.24.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §28.24 and Ch.28

►

28.24.4 $${\mathrm{Ms}}_{2m+1}^{(j)}(z,h)={(-1)}^m\sum _{\mathrm{\ell }=0}^{\mathrm{\infty }}{(-1)}^{\mathrm{\ell }}\frac{B_{2\mathrm{\ell }+1}^{2m+1}(h^2)}{B_{2s+1}^{2m+1}(h^2)}\left(J_{\mathrm{\ell }-s}\left(h{\mathrm{e}}^{-z}\right){𝒞}_{\mathrm{\ell }+s+1}^{(j)}(h{\mathrm{e}}^z)-J_{\mathrm{\ell }+s+1}\left(h{\mathrm{e}}^{-z}\right){𝒞}_{\mathrm{\ell }-s}^{(j)}(h{\mathrm{e}}^z)\right),$$

ⓘ

Symbols:

$J_{\nu }\left(z\right)$: Bessel function of the first kind, $\mathrm{e}$: base of natural logarithm, ${\mathrm{Ms}}_n^{(j)}(z,h)$: radial Mathieu function, $m$: integer, $h$: parameter, $j$: integer, $z$: complex variable, ${𝒞}_{\mu }^{(j)}$: cylinder functions and $B_m(q)$: Fourier coefficient

A&S Ref:

20.6.9

Permalink:

http://dlmf.nist.gov/28.24.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §28.24 and Ch.28

… ►For further power series of Mathieu radial functions of integer order for small parameters and improved convergence rate see Larsen et al. (2009).

8: 28.26 Asymptotic Approximations for Large $q$

… ►

28.26.1 $${\mathrm{Mc}}_m^{(3)}(z,h)=\frac{{\mathrm{e}}^{\mathrm{i}\varphi }}{{(\pi h\cosh z)}^{1/2}}\left({\mathrm{Fc}}_m(z,h)-\mathrm{i}{\mathrm{Gc}}_m(z,h)\right),$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\cosh z$: hyperbolic cosine function, $\mathrm{i}$: imaginary unit, ${\mathrm{Mc}}_n^{(j)}(z,h)$: radial Mathieu function, $m$: integer, $h$: parameter, $z$: complex variable and $\varphi$

A&S Ref:

20.9.7 (in slightly different notation)

Permalink:

http://dlmf.nist.gov/28.26.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §28.26(i), §28.26 and Ch.28

►

28.26.2 $$\mathrm{i}{\mathrm{Ms}}_{m+1}^{(3)}(z,h)=\frac{{\mathrm{e}}^{\mathrm{i}\varphi }}{{(\pi h\cosh z)}^{1/2}}\left({\mathrm{Fs}}_m(z,h)-\mathrm{i}{\mathrm{Gs}}_m(z,h)\right),$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\cosh z$: hyperbolic cosine function, $\mathrm{i}$: imaginary unit, ${\mathrm{Ms}}_n^{(j)}(z,h)$: radial Mathieu function, $m$: integer, $h$: parameter, $z$: complex variable and $\varphi$

A&S Ref:

20.9.7 (in slightly different notation)

Permalink:

http://dlmf.nist.gov/28.26.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §28.26(i), §28.26 and Ch.28

…

9: Bibliography B

… ►

Tables Relating to the Radial Mathieu Functions. Vol. 1: Functions of the First Kind. U.S. Government Printing Office, Washington, D.C..

ⓘ

External Links:

MathReview (C. J. Bouwkamp)

Referenced by:

1st item.

Encodings:

BibTeX

►

Tables Relating to the Radial Mathieu Functions. Vol. 2: Functions of the Second Kind. U.S. Government Printing Office, Washington, D.C..

ⓘ

External Links:

MathReview (C. J. Bouwkamp)

Referenced by:

2nd item, 1st item.

Encodings:

BibTeX

…

10: Bibliography L

… ►

New method to obtain small parameter power series expansions of Mathieu radial and angular functions. Math. Comp. 78 (265), pp. 255–274.

ⓘ

External Links:

ISSN 0025-5718, Document, FullText, MathReview (Junesang Choi), ZentralBlatt

Referenced by:

§28.24, §28.24.

Encodings:

BibTeX

…