parameters
(0.001 seconds)
1—10 of 386 matching pages
1: 31.13 Asymptotic Approximations
§31.13 Asymptotic Approximations
►For asymptotic approximations for the accessory parameter eigenvalues , see Fedoryuk (1991) and Slavyanov (1996). …2: 31.3 Basic Solutions
3: 29.11 Lamé Wave Equation
…
►
29.11.1
►in which is another parameter.
…
►For properties of the solutions of (29.11.1) see Arscott (1956, 1959), Arscott (1964b, Chapter X), Erdélyi et al. (1955, §16.14), Fedoryuk (1989), and Müller (1966a, b, c).
4: 31.14 General Fuchsian Equation
…
►
►The three sets of parameters comprise the singularity parameters
, the exponent parameters
, and the free accessory parameters
.
With and the total number of free parameters is .
…
►
31.14.1
.
…
►
31.14.3
…
5: 28.17 Stability as
§28.17 Stability as
►If all solutions of (28.2.1) are bounded when along the real axis, then the corresponding pair of parameters is called stable. … ►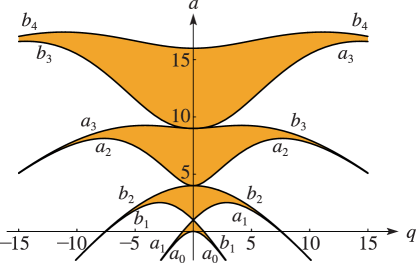 ►
►
6: 31.1 Special Notation
…
►
►
…
►Sometimes the parameters are suppressed.
| , | real variables. |
|---|---|
| … | |
| complex parameter, . | |
| complex parameters. | |
7: 34.8 Approximations for Large Parameters
§34.8 Approximations for Large Parameters
►For large values of the parameters in the , , and symbols, different asymptotic forms are obtained depending on which parameters are large. … ►and the symbol denotes a quantity that tends to zero as the parameters tend to infinity, as in §2.1(i). …8: 28.14 Fourier Series
9: 15.7 Continued Fractions
10: 31.6 Path-Multiplicative Solutions
…
►
31.6.1
,
…
