parabolic cylinder functions

SearchAdvancedHelp

(0.008 seconds)

11—20 of 60 matching pages

11: 12.2 Differential Equations

§12.2 Differential Equations

►

§12.2(i) Introduction

… ►

§12.2(iii) Wronskians

… ►

§12.2(iv) Reflection Formulas

… ►

§12.2(v) Connection Formulas

…

12: 12.3 Graphics

… ►

§12.3(i) Real Variables

… ►

►

►

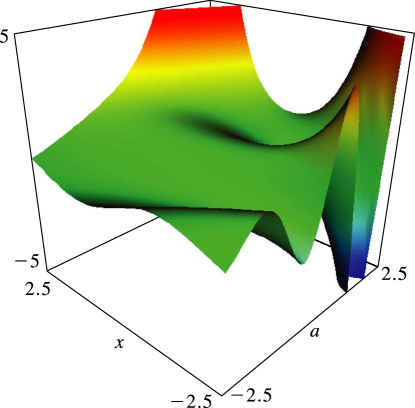
Figure 12.3.8: $V(a,x)$, $-2.5\le a\le 2.5$, $-2.5\le x\le 2.5$. Magnify 3D Help

►

§12.3(ii) Complex Variables

…

13: 12.12 Integrals

§12.12 Integrals

… ►

Nicholson-type Integral

►

12.12.4 $${(U(a,z))}^2+{(\overline{U}(a,z))}^2=\frac{2^{\frac{3}{2}}}{\pi }\mathrm{\Gamma }\left(\frac{1}{2}-a\right){\int }_0^{\mathrm{\infty }}\frac{{\mathrm{e}}^{2at+\frac{1}{2}{z}^2\tanh t}}{\sqrt{\sinh \left(2t\right)}}dt,$$ .

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\sinh z$: hyperbolic sine function, $\tanh z$: hyperbolic tangent function, $\int$: integral, $U(a,z)$: parabolic cylinder function, $\overline{U}(a,x)$: parabolic cylinder function, $\mathrm{\Re }$: real part, $z$: complex variable and $a$: real or complex parameter

Notes:

See Durand (1975).

Referenced by:

§12.12

Permalink:

http://dlmf.nist.gov/12.12.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §12.12, §12.12 and Ch.12

… ► ►See also Barr (1968) and Lowdon (1970).

14: 12.8 Recurrence Relations and Derivatives

… ►

§12.8(i) Recurrence Relations

… ►

12.8.2 $$U^{\prime }(a,z)+\frac{1}{2}zU(a,z)+(a+\frac{1}{2})U(a+1,z)=0,$$

ⓘ

Symbols:

$U(a,z)$: parabolic cylinder function, $z$: complex variable and $a$: real or complex parameter

A&S Ref:

19.6.1

Permalink:

http://dlmf.nist.gov/12.8.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §12.8(i), §12.8 and Ch.12

►

12.8.3 $$U^{\prime }(a,z)-\frac{1}{2}zU(a,z)+U(a-1,z)=0,$$

ⓘ

Symbols:

$U(a,z)$: parabolic cylinder function, $z$: complex variable and $a$: real or complex parameter

A&S Ref:

19.6.2

Permalink:

http://dlmf.nist.gov/12.8.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §12.8(i), §12.8 and Ch.12

… ►

12.8.6 $$V^{\prime }(a,z)-\frac{1}{2}zV(a,z)-(a-\frac{1}{2})V(a-1,z)=0,$$

ⓘ

Symbols:

$V(a,z)$: parabolic cylinder function, $z$: complex variable and $a$: real or complex parameter

A&S Ref:

19.6.5

Permalink:

http://dlmf.nist.gov/12.8.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §12.8(i), §12.8 and Ch.12

… ►

§12.8(ii) Derivatives

…

15: 12.13 Sums

§12.13 Sums

►

§12.13(i) Addition Theorems

►

12.13.1 $$U(a,x+y)={\mathrm{e}}^{\frac{1}{2}xy+\frac{1}{4}{y}^2}\sum _{m=0}^{\mathrm{\infty }}\frac{{(-y)}^m}{m!}U(a-m,x),$$

ⓘ

Symbols:

$\mathrm{e}$: base of natural logarithm, $!$: factorial (as in $n!$), $U(a,z)$: parabolic cylinder function, $x$: real variable, $y$: real variable and $a$: real or complex parameter

Referenced by:

§12.13(i)

Permalink:

http://dlmf.nist.gov/12.13.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §12.13(i), §12.13 and Ch.12

►

12.13.2 $$U(a,x+y)={\mathrm{e}}^{-\frac{1}{2}xy-\frac{1}{4}{y}^2}\sum _{m=0}^{\mathrm{\infty }}\left(\genfrac{}{}{0.0pt}{}{-a-\frac{1}{2}}{m}\right)y^{m}U(a+m,x),$$

ⓘ

Symbols:

$\left(\genfrac{}{}{0.0pt}{}{m}{n}\right)$: binomial coefficient, $\mathrm{e}$: base of natural logarithm, $U(a,z)$: parabolic cylinder function, $x$: real variable, $y$: real variable and $a$: real or complex parameter

Permalink:

http://dlmf.nist.gov/12.13.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §12.13(i), §12.13 and Ch.12

►

12.13.3 $$V(a,x+y)={\mathrm{e}}^{\frac{1}{2}xy+\frac{1}{4}{y}^2}\sum _{m=0}^{\mathrm{\infty }}\left(\genfrac{}{}{0.0pt}{}{a-\frac{1}{2}}{m}\right)y^{m}V(a-m,x),$$

ⓘ

Symbols:

$\left(\genfrac{}{}{0.0pt}{}{m}{n}\right)$: binomial coefficient, $\mathrm{e}$: base of natural logarithm, $V(a,z)$: parabolic cylinder function, $x$: real variable, $y$: real variable and $a$: real or complex parameter

Permalink:

http://dlmf.nist.gov/12.13.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §12.13(i), §12.13 and Ch.12

…

16: 10.39 Relations to Other Functions

… ►

Parabolic Cylinder Functions

… ►

10.39.3 $$K_{\frac{1}{4}}\left(z\right)={\pi }^{\frac{1}{2}}{z}^{-\frac{1}{4}}U(0,2z^{\frac{1}{2}}),$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $K_{\nu }\left(z\right)$: modified Bessel function of the second kind, $U(a,z)$: parabolic cylinder function and $z$: complex variable

Permalink:

http://dlmf.nist.gov/10.39.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §10.39, §10.39 and Ch.10

►

10.39.4 $$K_{\frac{3}{4}}\left(z\right)=\frac{1}{2}{\pi }^{\frac{1}{2}}{z}^{-\frac{3}{4}}\left(\frac{1}{2}U(1,2z^{\frac{1}{2}})+U(-1,2z^{\frac{1}{2}})\right).$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $K_{\nu }\left(z\right)$: modified Bessel function of the second kind, $U(a,z)$: parabolic cylinder function and $z$: complex variable

Permalink:

http://dlmf.nist.gov/10.39.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §10.39, §10.39 and Ch.10

…

17: 12.9 Asymptotic Expansions for Large Variable

§12.9 Asymptotic Expansions for Large Variable

… ►

12.9.1 $$U(a,z)\sim {\mathrm{e}}^{-\frac{1}{4}{z}^2}{z}^{-a-\frac{1}{2}}\sum _{s=0}^{\mathrm{\infty }}{(-1)}^s\frac{{\left(\frac{1}{2}+a\right)}_{2s}}{s!{(2z^2)}^s},$$ ,

ⓘ

Symbols:

${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $!$: factorial (as in $n!$), $U(a,z)$: parabolic cylinder function, $\mathrm{ph}$: phase, $z$: complex variable, $s$: nonnegative integer, $a$: real or complex parameter and $\delta$: arbitrary small positive constant

A&S Ref:

19.8.1 (modification of)

Referenced by:

§12.9(i), §12.9(ii)

Permalink:

http://dlmf.nist.gov/12.9.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §12.9(i), §12.9 and Ch.12

►

12.9.2 $$V(a,z)\sim \sqrt{\frac{2}{\pi }}{\mathrm{e}}^{\frac{1}{4}{z}^2}{z}^{a-\frac{1}{2}}\sum _{s=0}^{\mathrm{\infty }}\frac{{\left(\frac{1}{2}-a\right)}_{2s}}{s!{(2z^2)}^s},$$ .

ⓘ

Symbols:

${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $!$: factorial (as in $n!$), $V(a,z)$: parabolic cylinder function, $\mathrm{ph}$: phase, $z$: complex variable, $s$: nonnegative integer, $a$: real or complex parameter and $\delta$: arbitrary small positive constant

A&S Ref:

19.8.2 (modification of)

Referenced by:

§12.9(i), §12.9(ii)

Permalink:

http://dlmf.nist.gov/12.9.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §12.9(i), §12.9 and Ch.12

►

12.9.3 $$U(a,z)\sim {\mathrm{e}}^{-\frac{1}{4}{z}^2}{z}^{-a-\frac{1}{2}}\sum _{s=0}^{\mathrm{\infty }}{(-1)}^s\frac{{\left(\frac{1}{2}+a\right)}_{2s}}{s!{(2z^2)}^s}\pm \mathrm{i}\frac{\sqrt{2\pi }}{\mathrm{\Gamma }\left(\frac{1}{2}+a\right)}{\mathrm{e}}^{\mp \mathrm{i}\pi a}{\mathrm{e}}^{\frac{1}{4}{z}^2}{z}^{a-\frac{1}{2}}\sum _{s=0}^{\mathrm{\infty }}\frac{{\left(\frac{1}{2}-a\right)}_{2s}}{s!{(2z^2)}^s},$$ $\frac{1}{4}\pi +\delta \le \pm \mathrm{ph}z\le \frac{5}{4}\pi -\delta$ ,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $!$: factorial (as in $n!$), $\mathrm{i}$: imaginary unit, $U(a,z)$: parabolic cylinder function, $\mathrm{ph}$: phase, $z$: complex variable, $s$: nonnegative integer, $a$: real or complex parameter and $\delta$: arbitrary small positive constant

Permalink:

http://dlmf.nist.gov/12.9.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §12.9(i), §12.9 and Ch.12

… ►

§12.9(ii) Bounds and Re-Expansions for the Remainder Terms

…

18: 12.5 Integral Representations

… ►

§12.5(i) Integrals Along the Real Line

►

12.5.1 $$U(a,z)=\frac{{\mathrm{e}}^{-\frac{1}{4}{z}^2}}{\mathrm{\Gamma }\left(\frac{1}{2}+a\right)}{\int }_0^{\mathrm{\infty }}{t}^{a-\frac{1}{2}}{\mathrm{e}}^{-\frac{1}{2}{t}^2-zt}dt,$$ $\mathrm{\Re }a>-\frac{1}{2}$ ,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $U(a,z)$: parabolic cylinder function, $\mathrm{\Re }$: real part, $z$: complex variable and $a$: real or complex parameter

A&S Ref:

19.5.3 (modification of)

Referenced by:

§12.5(i), §12.8(ii), §36.2(ii)

Permalink:

http://dlmf.nist.gov/12.5.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §12.5(i), §12.5 and Ch.12

… ►

§12.5(ii) Contour Integrals

… ►

§12.5(iii) Mellin–Barnes Integrals

… ►

§12.5(iv) Compendia

…

19: 29.16 Asymptotic Expansions

… ►The approximating functions are exponential, trigonometric, and parabolic cylinder functions.

20: 12.4 Power-Series Expansions

§12.4 Power-Series Expansions

►

12.4.1 $$U(a,z)=U(a,0)u_1(a,z)+U^{\prime }(a,0)u_2(a,z),$$

ⓘ

Symbols:

$U(a,z)$: parabolic cylinder function, $z$: complex variable, $a$: real or complex parameter, $u_1(a,z)$: solution and $u_2(a,z)$: solution

Referenced by:

§12.20

Permalink:

http://dlmf.nist.gov/12.4.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §12.4 and Ch.12

►

12.4.2 $$V(a,z)=V(a,0)u_1(a,z)+V^{\prime }(a,0)u_2(a,z),$$

ⓘ

Symbols:

$V(a,z)$: parabolic cylinder function, $z$: complex variable, $a$: real or complex parameter, $u_1(a,z)$: solution and $u_2(a,z)$: solution

Referenced by:

§12.20

Permalink:

http://dlmf.nist.gov/12.4.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §12.4 and Ch.12

…