of canonical integrals
(0.003 seconds)
11—20 of 20 matching pages
11: 36.12 Uniform Approximation of Integrals
§36.12 Uniform Approximation of Integrals
… ►The canonical integrals (36.2.4) provide a basis for uniform asymptotic approximations of oscillatory integrals. … ►This technique can be applied to generate a hierarchy of approximations for the diffraction catastrophes in (36.2.10) away from , in terms of canonical integrals for . For example, the diffraction catastrophe defined by (36.2.10), and corresponding to the Pearcey integral (36.2.14), can be approximated by the Airy function when is large, provided that and are not small. … ►For further information concerning integrals with several coalescing saddle points see Arnol’d et al. (1988), Berry and Howls (1993, 1994), Bleistein (1967), Duistermaat (1974), Ludwig (1966), Olde Daalhuis (2000), and Ursell (1972, 1980).12: Errata
Scales were corrected in all figures. The interval was replaced by and replaced by . All plots and interactive visualizations were regenerated to improve image quality.
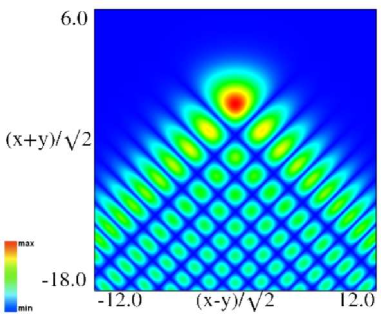 |
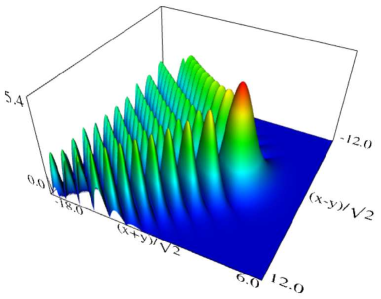 |
| (a) Density plot. | (b) 3D plot. |
Figure 36.3.9: Modulus of hyperbolic umbilic canonical integral function .
 |
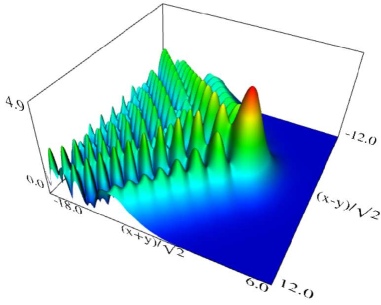 |
| (a) Density plot. | (b) 3D plot. |
Figure 36.3.10: Modulus of hyperbolic umbilic canonical integral function .
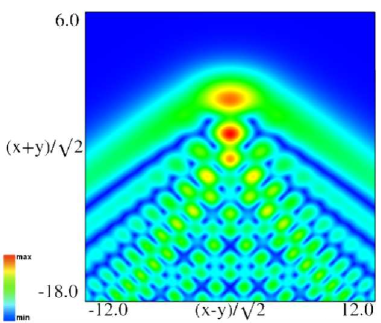 |
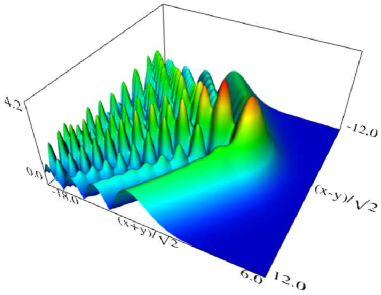 |
| (a) Density plot. | (b) 3D plot. |
Figure 36.3.11: Modulus of hyperbolic umbilic canonical integral function .
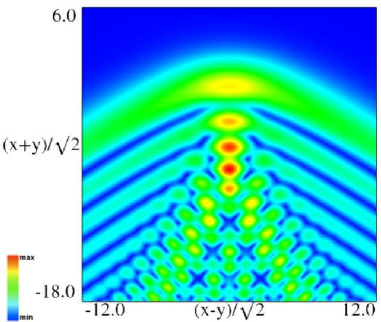 |
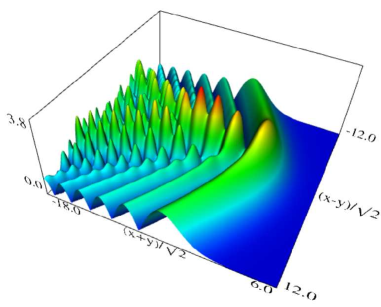 |
| (a) Density plot. | (b) 3D plot. |
Figure 36.3.12: Modulus of hyperbolic umbilic canonical integral function .
Reported 2016-09-12 by Dan Piponi.
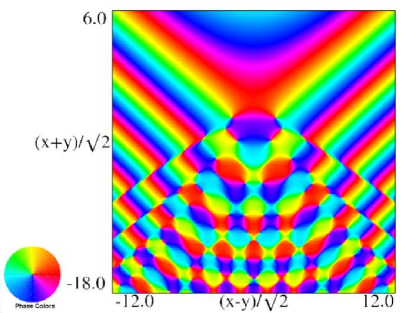
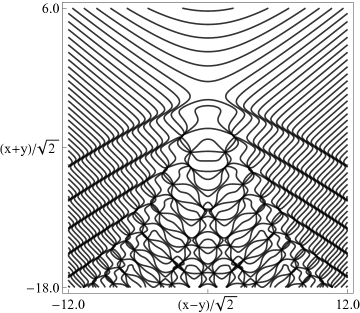
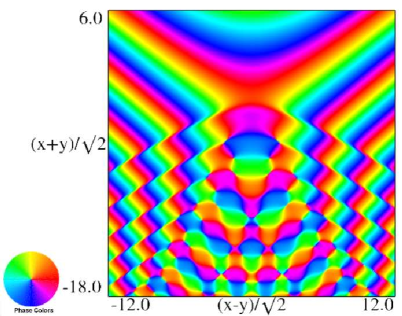
The scaling error reported on 2016-09-12 by Dan Piponi also applied to contour and density plots for the phase of the hyperbolic umbilic canonical integrals. Scales were corrected in all figures. The interval was replaced by and replaced by . All plots and interactive visualizations were regenerated to improve image quality.
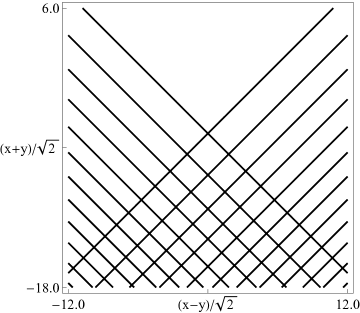 |
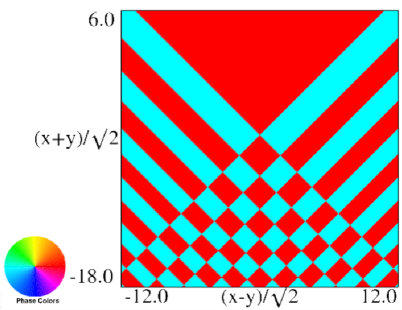 |
| (a) Contour plot. | (b) Density plot. |
Figure 36.3.18: Phase of hyperbolic umbilic canonical integral .
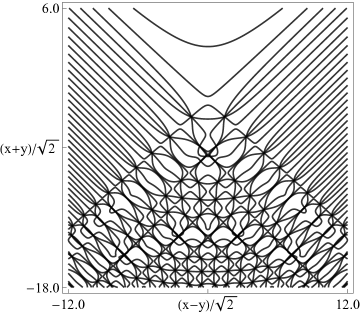 |
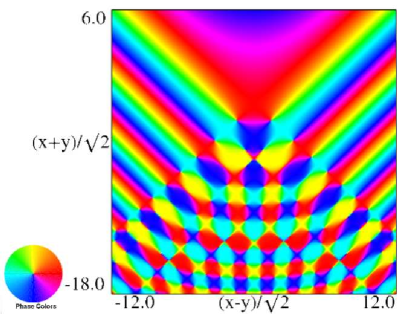 |
| (a) Contour plot. | (b) Density plot. |
Figure 36.3.19: Phase of hyperbolic umbilic canonical integral .
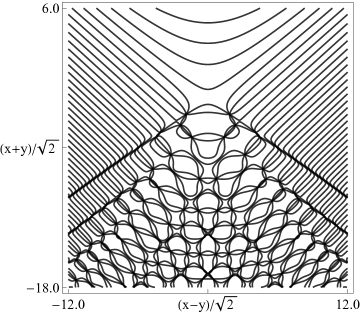 |
 |
| (a) Contour plot. | (b) Density plot. |
Figure 36.3.20: Phase of hyperbolic umbilic canonical integral .
 |
 |
| (a) Contour plot. | (b) Density plot. |
Figure 36.3.21: Phase of hyperbolic umbilic canonical integral .
Reported 2016-09-28.
Originally this equation appeared with in the second term, rather than .
Reported 2010-04-02.
13: 36.15 Methods of Computation
14: 36.5 Stokes Sets
§36.5(ii) Cuspoids
… ►§36.5(iii) Umbilics
… ►§36.5(iv) Visualizations
… ►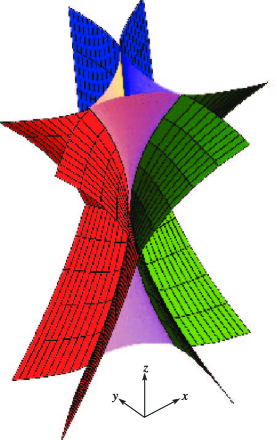 ►
►
 ►
►
