of logarithms

SearchAdvancedHelp

(0.003 seconds)

1—10 of 407 matching pages

1: 6.2 Definitions and Interrelations

… ►

§6.2(i) Exponential and Logarithmic Integrals

… ►As in the case of the logarithm (§4.2(i)) there is a cut along the interval $(-\mathrm{\infty },0]$ and the principal value is two-valued on $(-\mathrm{\infty },0)$. … ►

6.2.4 $$E_1\left(z\right)=\mathrm{Ein}\left(z\right)-\ln z-\gamma .$$

ⓘ

Symbols:

$\gamma$: Euler’s constant, $\mathrm{Ein}\left(z\right)$: complementary exponential integral, $E_1\left(z\right)$: exponential integral, $\ln z$: principal branch of logarithm function and $z$: complex variable

Referenced by:

§6.10(ii), §6.4

Permalink:

http://dlmf.nist.gov/6.2.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §6.2(i), §6.2 and Ch.6

… ►The logarithmic integral is defined by ►

6.2.8 $$\mathrm{li}\left(x\right)={⨍}_0^x\frac{dt}{\ln t}=\mathrm{Ei}\left(\ln x\right),$$ $x>1$.

ⓘ

Defines:

$\mathrm{li}\left(x\right)$: logarithmic integral

Symbols:

$dx$: differential of $x$ , $\mathrm{Ei}\left(x\right)$: exponential integral, $\ln z$: principal branch of logarithm function, ${⨍}_a^b$: Cauchy principal value and $x$: real variable

A&S Ref:

5.1.3

Referenced by:

§27.12, §6.12(i)

Permalink:

http://dlmf.nist.gov/6.2.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §6.2(i), §6.2 and Ch.6

…

2: 4.11 Sums

§4.11 Sums

►For infinite series involving logarithms and/or exponentials, see Gradshteyn and Ryzhik (2000, Chapter 1), Hansen (1975, §44), and Prudnikov et al. (1986a, Chapter 5).

3: 4.12 Generalized Logarithms and Exponentials

§4.12 Generalized Logarithms and Exponentials

►A generalized exponential function $\varphi (x)$ satisfies the equations …Its inverse $\psi (x)$ is called a generalized logarithm. It, too, is strictly increasing when $0\le x\le 1$, and … ►For analytic generalized logarithms, see Kneser (1950).

4: 4.2 Definitions

… ►

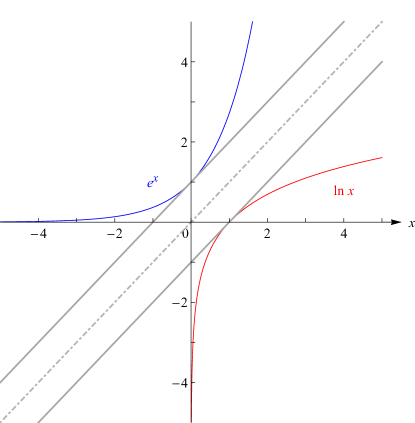
§4.2(i) The Logarithm

►The general logarithm function $\mathrm{Ln}z$ is defined by … ► … ►

§4.2(ii) Logarithms to a General Base $a$

… ►Natural logarithms have as base the unique positive number …

5: 4.10 Integrals

… ►

§4.10(i) Logarithms

… ►

4.10.4 $$\int \frac{dz}{z\ln z}=\ln \left(\ln z\right),$$

ⓘ

Symbols:

$dx$: differential of $x$ , $\int$: integral, $\ln z$: principal branch of logarithm function and $z$: complex variable

A&S Ref:

4.1.52

Referenced by:

§4.10(i)

Permalink:

http://dlmf.nist.gov/4.10.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §4.10(i), §4.10 and Ch.4

… ►

4.10.7 $${⨍}_0^x\frac{dt}{\ln t}=\mathrm{li}\left(x\right),$$ $x>1$.

ⓘ

Symbols:

$dx$: differential of $x$ , $\mathrm{li}\left(x\right)$: logarithmic integral, $\ln z$: principal branch of logarithm function, ${⨍}_a^b$: Cauchy principal value and $x$: real variable

A&S Ref:

4.1.57

Referenced by:

§4.10(i)

Permalink:

http://dlmf.nist.gov/4.10.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §4.10(i), §4.10 and Ch.4

… ►For $\mathrm{li}\left(x\right)$ see §6.2(i). … ►Extensive compendia of indefinite and definite integrals of logarithms and exponentials include Apelblat (1983, pp. 16–47), Bierens de Haan (1939), Gröbner and Hofreiter (1949, pp. 107–116), Gröbner and Hofreiter (1950, pp. 52–90), Gradshteyn and Ryzhik (2000, Chapters 2–4), and Prudnikov et al. (1986a, §§1.3, 1.6, 2.3, 2.6).

6: 4.8 Identities

… ►

§4.8(i) Logarithms

… ►

4.8.1 $$\mathrm{Ln}\left(z_1{z}_2\right)=\mathrm{Ln}{z}_1+\mathrm{Ln}{z}_2.$$

ⓘ

Symbols:

$\mathrm{Ln}z$: general logarithm function and $z$: complex variable

A&S Ref:

4.1.6

Referenced by:

§4.8(i)

Permalink:

http://dlmf.nist.gov/4.8.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §4.8(i), §4.8 and Ch.4

►This is interpreted that every value of $\mathrm{Ln}\left(z_1{z}_2\right)$ is one of the values of $\mathrm{Ln}{z}_1+\mathrm{Ln}{z}_2$, and vice versa. … ►

4.8.10 $$\exp \left(\ln z\right)=\exp \left(\mathrm{Ln}z\right)=z.$$

ⓘ

Symbols:

$\exp z$: exponential function, $\mathrm{Ln}z$: general logarithm function, $\ln z$: principal branch of logarithm function and $z$: complex variable

A&S Ref:

4.2.4

Referenced by:

(25.10.2), §4.8(i)

Permalink:

http://dlmf.nist.gov/4.8.E10

Encodings:

pMML, png, TeX

See also:

Annotations for §4.8(i), §4.8 and Ch.4

… ►

4.8.13 $$\ln \left(a^x\right)=x\ln a,$$ $a>0$.

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function, $a$: real or complex constant and $x$: real variable

Permalink:

http://dlmf.nist.gov/4.8.E13

Encodings:

pMML, png, TeX

See also:

Annotations for §4.8(i), §4.8 and Ch.4

…

7: 5.10 Continued Fractions

§5.10 Continued Fractions

… ►

5.10.1 $$\mathrm{Ln}\mathrm{\Gamma }\left(z\right)+z-\left(z-\frac{1}{2}\right)\ln z-\frac{1}{2}\ln \left(2\pi \right)=\frac{a_0}{z+}\frac{a_1}{z+}\frac{a_2}{z+}\frac{a_3}{z+}\frac{a_4}{z+}\frac{a_5}{z+}\mathrm{\cdots },$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{Ln}z$: general logarithm function, $\ln z$: principal branch of logarithm function, $z$: complex variable and $a_k$: coefficient

Referenced by:

Erratum (V1.0.10) for Equations (5.9.10), (5.9.11), (5.10.1), (5.11.1), (5.11.8)

Permalink:

http://dlmf.nist.gov/5.10.E1

Encodings:

pMML, png, TeX

Addition (effective with 1.0.10):

To increase the region of validity of this equation, the logarithm of the gamma function that appears on its left-hand side has been changed to $\mathrm{Ln}\mathrm{\Gamma }\left(z\right)$, where $\mathrm{Ln}$ is the general logarithm. Originally $\ln \mathrm{\Gamma }\left(z\right)$ was used, where $\ln$ is the principal branch of the logarithm.

Suggested 2015-02-13 by Philippe Spindel

See also:

Annotations for §5.10 and Ch.5

…

8: 27.12 Asymptotic Formulas: Primes

… ►

27.12.1 $$\underset{n\to \mathrm{\infty }}{lim}\frac{p_n}{n\ln n}=1,$$

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function, $n$: positive integer and $p,p_1,\mathrm{\dots }$: prime numbers

Permalink:

http://dlmf.nist.gov/27.12.E1

Encodings:

pMML, png, TeX

Change of Notation (effective with 1.0.10):

The notation for logarithm has been changed to $\ln$ from $\log$.

See also:

Annotations for §27.12 and Ch.27

►

27.12.2 $$p_n>n\ln n,$$ $n=1,2,\mathrm{\dots }$.

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function, $n$: positive integer and $p,p_1,\mathrm{\dots }$: prime numbers

Permalink:

http://dlmf.nist.gov/27.12.E2

Encodings:

pMML, png, TeX

Change of Notation (effective with 1.0.10):

The notation for logarithm has been changed to $\ln$ from $\log$.

See also:

Annotations for §27.12 and Ch.27

… ►For the logarithmic integral $\mathrm{li}\left(x\right)$ see (6.2.8). … ► $\pi \left(x\right)-\mathrm{li}\left(x\right)$ changes sign infinitely often as $x\to \mathrm{\infty }$; see Littlewood (1914), Bays and Hudson (2000). … ►

27.12.7

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{li}\left(x\right)$: logarithmic integral, $\ln z$: principal branch of logarithm function, $\pi \left(x\right)$: number of primes not exceeding a number and $x$: real number

Referenced by:

§27.12

Permalink:

http://dlmf.nist.gov/27.12.E7

Encodings:

pMML, png, TeX

Change of Notation (effective with 1.0.10):

The notation for logarithm has been changed to $\ln$ from $\log$.

See also:

Annotations for §27.12, §27.12 and Ch.27

…

9: 4.44 Other Applications

§4.44 Other Applications

►The Einstein functions and Planck’s radiation function are elementary combinations of exponentials, or exponentials and logarithms. … ►For applications of generalized exponentials and generalized logarithms to computer arithmetic see §3.1(iv). …

10: 4.3 Graphics

… ►

►►

Figure 4.3.1: $\ln x$ and ${\mathrm{e}}^x$. … Magnify

►

§4.3(ii) Complex Arguments: Conformal Maps

… ►

► … ►

Figure 4.3.2: Conformal mapping of exponential and logarithm. … Magnify

… ►

►

►

Figure 4.3.3: $\ln \left(x+\mathrm{i}y\right)$ (principal value). … Magnify 3D Help

…