multivalued

SearchAdvancedHelp

(0.002 seconds)

11—20 of 37 matching pages

11: 4.15 Graphics

… ►

►►

Figure 4.15.2: $\mathrm{Arcsin}x$ and $\mathrm{Arccos}x$. … Magnify

…

12: 1.10 Functions of a Complex Variable

… ►

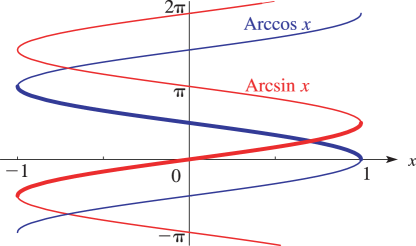
§1.10(vi) Multivalued Functions

… ►Let $F(z)$ be a multivalued function and $D$ be a domain. … ►Branches can be constructed in two ways: … ► ►

Example

…

13: 22.14 Integrals

… ►

22.14.2 $$\int \mathrm{cn}(x,k)dx=k^{-1}\mathrm{Arccos}\left(\mathrm{dn}(x,k)\right),$$

ⓘ

Symbols:

$\mathrm{cn}(z,k)$: Jacobian elliptic function, $\mathrm{dn}(z,k)$: Jacobian elliptic function, $dx$: differential of $x$ , $\int$: integral, $\mathrm{Arccos}z$: general arccosine function, $x$: real and $k$: modulus

A&S Ref:

16.24.2

Permalink:

http://dlmf.nist.gov/22.14.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §22.14(i), §22.14 and Ch.22

►

22.14.3 $$\int \mathrm{dn}(x,k)dx=\mathrm{Arcsin}\left(\mathrm{sn}(x,k)\right)=\mathrm{am}(x,k).$$

ⓘ

Symbols:

$\mathrm{am}(x,k)$: Jacobi’s amplitude function, $\mathrm{dn}(z,k)$: Jacobian elliptic function, $\mathrm{sn}(z,k)$: Jacobian elliptic function, $dx$: differential of $x$ , $\int$: integral, $\mathrm{Arcsin}z$: general arcsine function, $x$: real and $k$: modulus

A&S Ref:

16.24.3

Permalink:

http://dlmf.nist.gov/22.14.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §22.14(i), §22.14 and Ch.22

… ►

22.14.5 $$\int \mathrm{sd}(x,k)dx={(k{k}^{\prime })}^{-1}\mathrm{Arcsin}\left(-k\mathrm{cd}(x,k)\right),$$

ⓘ

Symbols:

$\mathrm{cd}(z,k)$: Jacobian elliptic function, $\mathrm{sd}(z,k)$: Jacobian elliptic function, $dx$: differential of $x$ , $\int$: integral, $\mathrm{Arcsin}z$: general arcsine function, $x$: real, $k$: modulus and $k^{\prime }$: complementary modulus

A&S Ref:

16.24.5

Permalink:

http://dlmf.nist.gov/22.14.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §22.14(i), §22.14 and Ch.22

►

22.14.6 $$\int \mathrm{nd}(x,k)dx=k_{}^{\prime }{}_{}{}^{-1}\mathrm{Arccos}\left(\mathrm{cd}(x,k)\right).$$

ⓘ

Symbols:

$\mathrm{cd}(z,k)$: Jacobian elliptic function, $\mathrm{nd}(z,k)$: Jacobian elliptic function, $dx$: differential of $x$ , $\int$: integral, $\mathrm{Arccos}z$: general arccosine function, $x$: real, $k$: modulus and $k^{\prime }$: complementary modulus

A&S Ref:

16.24.6

Permalink:

http://dlmf.nist.gov/22.14.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §22.14(i), §22.14 and Ch.22

…

14: 5.9 Integral Representations

… ►

5.9.10 $$\mathrm{Ln}\mathrm{\Gamma }\left(z\right)=\left(z-\frac{1}{2}\right)\ln z-z+\frac{1}{2}\ln \left(2\pi \right)+2{\int }_0^{\mathrm{\infty }}\frac{\arctan \left(t/z\right)}{{\mathrm{e}}^{2\pi t}-1}dt,$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $\arctan z$: arctangent function, $\mathrm{Ln}z$: general logarithm function, $\ln z$: principal branch of logarithm function and $z$: complex variable

A&S Ref:

6.1.50

Referenced by:

(5.9.10_1), §5.9(i), §5.9(ii), Erratum (V1.0.10) for Equations (5.9.10), (5.9.11), (5.10.1), (5.11.1), (5.11.8)

Permalink:

http://dlmf.nist.gov/5.9.E10

Encodings:

pMML, png, TeX

Addition (effective with 1.0.10):

To increase the region of validity of this equation, the logarithm of the gamma function that appears on its left-hand side has been changed to $\mathrm{Ln}\mathrm{\Gamma }\left(z\right)$, where $\mathrm{Ln}$ is the general logarithm. Originally $\ln \mathrm{\Gamma }\left(z\right)$ was used, where $\ln$ is the principal branch of the logarithm.

Suggested 2015-02-13 by Philippe Spindel

See also:

Annotations for §5.9(i), §5.9(i), §5.9 and Ch.5

… ►

5.9.10_1 $$\mathrm{Ln}\mathrm{\Gamma }\left(z\right)=\left(z-\frac{1}{2}\right)\ln z-z+\frac{1}{2}\ln \left(2\pi \right)-\frac{z}{\pi }{\int }_0^{\mathrm{\infty }}\frac{\ln \left(1-{\mathrm{e}}^{-2\pi t}\right)}{t^2+z^2}dt,$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $\mathrm{Ln}z$: general logarithm function, $\ln z$: principal branch of logarithm function and $z$: complex variable

Proof sketch:

Can be obtained from (5.9.10) via integration by parts.

Referenced by:

§5.9(i), Erratum (V1.1.7) for Additions

Permalink:

http://dlmf.nist.gov/5.9.E10_1

Encodings:

pMML, png, TeX

Addition (effective with 1.1.7):

This equation was added.

See also:

Annotations for §5.9(i), §5.9(i), §5.9 and Ch.5

►

5.9.10_2 $$\mathrm{Ln}\mathrm{\Gamma }\left(z\right)=\left(z-\frac{1}{2}\right)\ln z-z+\frac{1}{2}\ln \left(2\pi \right)+{\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-zt}\left(\frac{1}{{\mathrm{e}}^t-1}-\frac{1}{t}+\frac{1}{2}\right)\frac{dt}{t},$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $\mathrm{Ln}z$: general logarithm function, $\ln z$: principal branch of logarithm function and $z$: complex variable

Source:

Whittaker and Watson (1927, §12.31)

Referenced by:

§5.9(i), Erratum (V1.1.7) for Additions

Permalink:

http://dlmf.nist.gov/5.9.E10_2

Encodings:

pMML, png, TeX

Addition (effective with 1.1.7):

This equation was added.

See also:

Annotations for §5.9(i), §5.9(i), §5.9 and Ch.5

… ►

5.9.11 $$\mathrm{Ln}\mathrm{\Gamma }\left(z+1\right)=-\gamma z-\frac{1}{2\pi \mathrm{i}}{\int }_{-c-\mathrm{\infty }\mathrm{i}}^{-c+\mathrm{\infty }\mathrm{i}}\frac{\pi z^{-s}}{s\sin \left(\pi s\right)}\zeta \left(-s\right)ds,$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\gamma$: Euler’s constant, $\zeta \left(s\right)$: Riemann zeta function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{i}$: imaginary unit, $\int$: integral, $\mathrm{Ln}z$: general logarithm function, $\ln z$: principal branch of logarithm function, $\sin z$: sine function, $s$: real or complex variable and $z$: complex variable

Referenced by:

§5.9(i), §5.9(ii), Erratum (V1.0.10) for Equations (5.9.10), (5.9.11), (5.10.1), (5.11.1), (5.11.8)

Permalink:

http://dlmf.nist.gov/5.9.E11

Encodings:

pMML, png, TeX

Addition (effective with 1.0.10):

To increase the region of validity of this equation, the logarithm of the gamma function that appears on its left-hand side has been changed to $\mathrm{Ln}\mathrm{\Gamma }\left(z+1\right)$, where $\mathrm{Ln}$ is the general logarithm. Originally $\ln \mathrm{\Gamma }\left(z+1\right)$ was used, where $\ln$ is the principal branch of the logarithm.

Suggested 2015-02-13 by Philippe Spindel

See also:

Annotations for §5.9(i), §5.9(i), §5.9 and Ch.5

…

15: 5.11 Asymptotic Expansions

… ►

5.11.1 $$\mathrm{Ln}\mathrm{\Gamma }\left(z\right)\sim \left(z-\frac{1}{2}\right)\ln z-z+\frac{1}{2}\ln \left(2\pi \right)+\sum _{k=1}^{\mathrm{\infty }}\frac{B_{2k}}{2k(2k-1)z^{2k-1}}$$

ⓘ

Symbols:

$B_n$: Bernoulli numbers, $\mathrm{\Gamma }\left(z\right)$: gamma function, $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{Ln}z$: general logarithm function, $\ln z$: principal branch of logarithm function, $k$: nonnegative integer and $z$: complex variable

A&S Ref:

6.1.40

Referenced by:

§5.11(i), §5.11(i), §5.11(ii), §5.11(ii), Erratum (V1.0.10) for Equations (5.9.10), (5.9.11), (5.10.1), (5.11.1), (5.11.8)

Permalink:

http://dlmf.nist.gov/5.11.E1

Encodings:

pMML, png, TeX

Addition (effective with 1.0.10):

To increase the region of validity of this equation, the logarithm of the gamma function that appears on its left-hand side has been changed to $\mathrm{Ln}\mathrm{\Gamma }\left(z\right)$, where $\mathrm{Ln}$ is the general logarithm. Originally $\ln \mathrm{\Gamma }\left(z\right)$ was used, where $\ln$ is the principal branch of the logarithm.

Suggested 2015-02-13 by Philippe Spindel

See also:

Annotations for §5.11(i), §5.11 and Ch.5

… ►

5.11.8 $$\mathrm{Ln}\mathrm{\Gamma }\left(z+h\right)\sim \left(z+h-\frac{1}{2}\right)\ln z-z+\frac{1}{2}\ln \left(2\pi \right)+\sum _{k=2}^{\mathrm{\infty }}\frac{{(-1)}^k{B}_k\left(h\right)}{k(k-1)z^{k-1}},$$

ⓘ

Symbols:

$B_n\left(x\right)$: Bernoulli polynomials, $\mathrm{\Gamma }\left(z\right)$: gamma function, $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $[a,b]$: closed interval, $\mathrm{Ln}z$: general logarithm function, $\ln z$: principal branch of logarithm function, $k$: nonnegative integer and $z$: complex variable

Referenced by:

§12.10(ii), (5.11.8), §5.11(i), §5.11(ii), Erratum (V1.0.10) for Equations (5.9.10), (5.9.11), (5.10.1), (5.11.1), (5.11.8), Erratum (V1.0.11) for Equation (5.11.8)

Permalink:

http://dlmf.nist.gov/5.11.E8

Encodings:

pMML, png, TeX

Generalization (effective with 1.0.11):

Originally $h$ in (5.11.8) was unnecessarily restricted to lie in the interval $[0,1]$. In fact, $h$ may lie anywhere in the complex plane.

Suggested 2015-02-28 by Nico Temme

Addition (effective with 1.0.10):

To increase the region of validity of this equation, the logarithm of the gamma function that appears on its left-hand side has been changed to $\mathrm{Ln}\mathrm{\Gamma }\left(z+h\right)$, where $\mathrm{Ln}$ is the general logarithm. Originally $\ln \mathrm{\Gamma }\left(z+h\right)$ was used, where $\ln$ is the principal branch of the logarithm.

Suggested 2015-02-13 by Philippe Spindel

See also:

Annotations for §5.11(i), §5.11(i), §5.11 and Ch.5

…

16: 6.4 Analytic Continuation

… ►

6.4.1 $$E_1\left(z\right)=\mathrm{Ein}\left(z\right)-\mathrm{Ln}z-\gamma ;$$

ⓘ

Symbols:

$\gamma$: Euler’s constant, $\mathrm{Ein}\left(z\right)$: complementary exponential integral, $E_1\left(z\right)$: exponential integral, $\mathrm{Ln}z$: general logarithm function and $z$: complex variable

Referenced by:

§6.4

Permalink:

http://dlmf.nist.gov/6.4.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §6.4 and Ch.6

…

17: 14.25 Integral Representations

… ►where the multivalued functions have their principal values when and are continuous in $ℂ\setminus (-\mathrm{\infty },1]$. …

18: 19.21 Connection Formulas

… ►

19.21.7 $$(x-y)R_D(y,z,x)+(z-y)R_D(x,y,z)=3R_F(x,y,z)-3y^{1/2}{x}^{-1/2}{z}^{-1/2},$$

ⓘ

Symbols:

$R_D(x,y,z)$: elliptic integral symmetric in only two variables and $R_F(x,y,z)$: symmetric elliptic integral of first kind

Referenced by:

§19.21(ii), §19.25(i), Erratum (V1.1.3) for Chapter 19

Permalink:

http://dlmf.nist.gov/19.21.E7

Encodings:

pMML, png, TeX

Correction (effective with 1.1.3):

The factors inside the square root on the right-hand side were written as products to ensure the correct multivalued behavior.

Suggested 2021-06-07 by Luc Maisonobe

See also:

Annotations for §19.21(ii), §19.21 and Ch.19

… ►

19.21.8 $$R_D(y,z,x)+R_D(z,x,y)+R_D(x,y,z)=3x^{-1/2}{y}^{-1/2}{z}^{-1/2},$$

ⓘ

Symbols:

$R_D(x,y,z)$: elliptic integral symmetric in only two variables

Referenced by:

§19.21(ii), §19.33(iii), Erratum (V1.1.3) for Chapter 19

Permalink:

http://dlmf.nist.gov/19.21.E8

Encodings:

pMML, png, TeX

Correction (effective with 1.1.3):

The factors inside the square root on the right-hand side were written as products to ensure the correct multivalued behavior.

Suggested 2021-06-07 by Luc Maisonobe

See also:

Annotations for §19.21(ii), §19.21 and Ch.19

… ►

19.21.10 $$2R_G(x,y,z)=z{R}_F(x,y,z)-\frac{1}{3}(x-z)(y-z)R_D(x,y,z)+x^{1/2}{y}^{1/2}{z}^{-1/2},$$ $z\ne 0$.

ⓘ

Symbols:

$R_D(x,y,z)$: elliptic integral symmetric in only two variables, $R_F(x,y,z)$: symmetric elliptic integral of first kind and $R_G(x,y,z)$: symmetric elliptic integral of second kind

Referenced by:

§19.20(ii), §19.21(i), §19.21(ii), §19.21(ii), §19.36(i), §19.36(ii), Erratum (V1.1.3) for Chapter 19, Erratum (V1.1.7) for Equation (19.21.10)

Permalink:

http://dlmf.nist.gov/19.21.E10

Encodings:

pMML, png, TeX

Correction (effective with 1.1.7):

An incorrect factor of 3 was removed in the last term on the right-hand side.

Suggested 2022-06-27 by Abdulhafeez Abdulsalam

Correction (effective with 1.1.3):

The factors inside the square root on the right-hand side were written as products to ensure the correct multivalued behavior.

Suggested 2021-06-07 by Luc Maisonobe

See also:

Annotations for §19.21(ii), §19.21 and Ch.19

…

19: 14.1 Special Notation

… ►Multivalued functions take their principal values (§4.2(i)) unless indicated otherwise. …

20: 14.21 Definitions and Basic Properties

… ►When $z$ is complex $P_{\nu }^{\pm \mu }\left(z\right)$, $Q_{\nu }^{\mu }\left(z\right)$, and ${𝑸}_{\nu }^{\mu }\left(z\right)$ are defined by (14.3.6)–(14.3.10) with $x$ replaced by $z$: the principal branches are obtained by taking the principal values of all the multivalued functions appearing in these representations when $z\in (1,\mathrm{\infty })$, and by continuity elsewhere in the $z$-plane with a cut along the interval $(-\mathrm{\infty },1]$; compare §4.2(i). …