modular functions

SearchAdvancedHelp

(0.003 seconds)

1—10 of 44 matching pages

1: 23.15 Definitions

§23.15 Definitions

►

§23.15(i) General Modular Functions

… ►

Elliptic Modular Function

… ►

Dedekind’s Eta Function (or Dedekind Modular Function)

… ►

2: 23.16 Graphics

§23.16 Graphics

►See Figures 23.16.1–23.16.3 for the modular functions 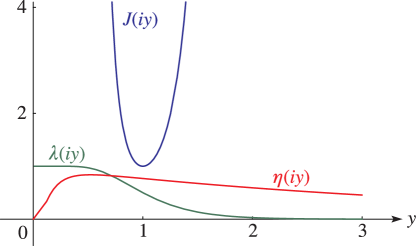$\lambda$, $J$, and $\eta$. … ►

►►

Figure 23.16.1: Modular functions $\lambda \left(\mathrm{i}y\right)$, $J\left(\mathrm{i}y\right)$, $\eta \left(\mathrm{i}y\right)$ for $0\le y\le 3$. … Magnify

►

►

►

Figure 23.16.2: Elliptic modular function $\lambda \left(x+\mathrm{i}y\right)$ for $-0.25\le x\le 0.25$, $0.005\le y\le 0.1$. Magnify 3D Help

►

►

►

Figure 23.16.3: Dedekind’s eta function $\eta \left(x+\mathrm{i}y\right)$ for $-0.0625\le x\le 0.0625$, $0.0001\le y\le 0.07$. Magnify 3D Help

3: 23.17 Elementary Properties

§23.17 Elementary Properties

►

§23.17(i) Special Values

… ►

§23.17(ii) Power and Laurent Series

… ►

23.17.4 $$\lambda \left(\tau \right)=16q(1-8q+44q^2+\mathrm{\cdots }),$$

ⓘ

Symbols:

$\lambda \left(\tau \right)$: elliptic modular function, $q$: nome and $\tau$: complex variable

Permalink:

http://dlmf.nist.gov/23.17.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §23.17(ii), §23.17 and Ch.23

… ►

§23.17(iii) Infinite Products

…

4: 23.19 Interrelations

§23.19 Interrelations

►

23.19.1 $$\lambda \left(\tau \right)=16{\left(\frac{{\eta }^2\left(2\tau \right)\eta \left(\frac{1}{2}\tau \right)}{{\eta }^3\left(\tau \right)}\right)}^8,$$

ⓘ

Symbols:

$\eta \left(\tau \right)$: Dedekind’s eta function (or Dedekind modular function), $\lambda \left(\tau \right)$: elliptic modular function and $\tau$: complex variable

Permalink:

http://dlmf.nist.gov/23.19.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §23.19 and Ch.23

►

23.19.2 $$J\left(\tau \right)=\frac{4}{27}\frac{{\left(1-\lambda \left(\tau \right)+{\lambda }^2\left(\tau \right)\right)}^3}{{\left(\lambda \left(\tau \right)\left(1-\lambda \left(\tau \right)\right)\right)}^2},$$

ⓘ

Symbols:

$J\left(\tau \right)$: Klein’s complete invariant, $\lambda \left(\tau \right)$: elliptic modular function and $\tau$: complex variable

Permalink:

http://dlmf.nist.gov/23.19.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §23.19 and Ch.23

… ►

23.19.4 $$\mathrm{\Delta }={(2\pi )}^{12}{\eta }^{24}\left(\tau \right).$$

ⓘ

Symbols:

$\eta \left(\tau \right)$: Dedekind’s eta function (or Dedekind modular function), $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{\Delta }$: discriminant and $\tau$: complex variable

Referenced by:

§23.19

Permalink:

http://dlmf.nist.gov/23.19.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §23.19 and Ch.23

5: 23.1 Special Notation

… ►The main functions treated in this chapter are the Weierstrass $\mathrm{\wp }$-function $\mathrm{\wp }\left(z\right)=\mathrm{\wp }\left(z|𝕃\right)=\mathrm{\wp }(z;g_2,g_3)$; the Weierstrass zeta function $\zeta \left(z\right)=\zeta \left(z|𝕃\right)=\zeta (z;g_2,g_3)$; the Weierstrass sigma function $\sigma \left(z\right)=\sigma \left(z|𝕃\right)=\sigma (z;g_2,g_3)$; the elliptic modular function $\lambda \left(\tau \right)$; Klein’s complete invariant $J\left(\tau \right)$; Dedekind’s eta function $\eta \left(\tau \right)$. …

6: 23.21 Physical Applications

§23.21 Physical Applications

… ►

§23.21(iv) Modular Functions

►Physical applications of modular functions include: … ►

String theory. See Green et al. (1988a, §8.2) and Polchinski (1998, §7.2).

7: 23 Weierstrass Elliptic and Modular
Functions

Chapter 23 Weierstrass Elliptic and Modular Functions

…

8: 23.18 Modular Transformations

§23.18 Modular Transformations

►

Elliptic Modular Function

… ►

23.18.3 $$\lambda \left(𝒜\tau \right)=\lambda \left(\tau \right),$$

ⓘ

Symbols:

$\lambda \left(\tau \right)$: elliptic modular function, $\tau$: complex variable and $𝒜$: bilinear transformation

Permalink:

http://dlmf.nist.gov/23.18.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §23.18, §23.18 and Ch.23

… ►

23.18.5 $$\eta \left(𝒜\tau \right)=\epsilon (𝒜){\left(-\mathrm{i}(c\tau +d)\right)}^{1/2}\eta \left(\tau \right),$$

ⓘ

Symbols:

$\eta \left(\tau \right)$: Dedekind’s eta function (or Dedekind modular function), $\mathrm{i}$: imaginary unit, $\tau$: complex variable, $𝒜$: bilinear transformation, $c$: integer, $d$: integer and $\epsilon (𝒜)$: function

Permalink:

http://dlmf.nist.gov/23.18.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §23.18, §23.18 and Ch.23

…

9: 23.20 Mathematical Applications

… ►For conformal mappings via modular functions see Apostol (1990, §2.7). … ►

§23.20(iv) Modular and Quintic Equations

… ►

§23.20(v) Modular Functions and Number Theory

… ►

10: Peter L. Walker

… ►

23 Weierstrass Elliptic and Modular Functions

…