modified spherical Bessel functions

SearchAdvancedHelp

(0.018 seconds)

1—10 of 34 matching pages

1: 10.48 Graphs

§10.48 Graphs

… ►

►►

Figure 10.48.5: ${𝗂}_0^{(1)}\left(x\right)$, ${𝗂}_0^{(2)}\left(x\right)$, ${𝗄}_0\left(x\right)$, $0\le x\le 4$. Magnify

►

►►

Figure 10.48.6: ${𝗂}_1^{(1)}\left(x\right),{𝗂}_1^{(2)}\left(x\right),{𝗄}_1\left(x\right)$, $0\le x\le 4$. Magnify

►

►►

Figure 10.48.7: ${𝗂}_5^{(1)}\left(x\right)$, ${𝗂}_5^{(2)}\left(x\right)$, ${𝗄}_5\left(x\right)$, $0\le x\le 8$. Magnify

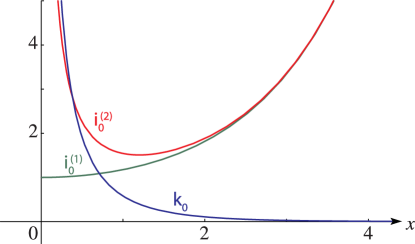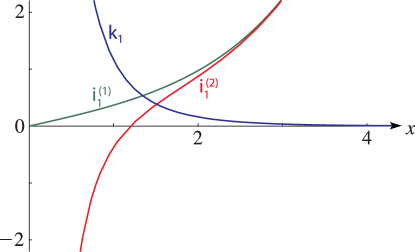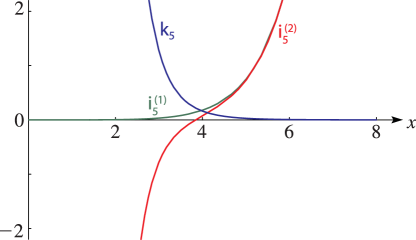2: 10.52 Limiting Forms

… ►

10.52.1 $${𝗃}_n\left(z\right),{𝗂}_n^{(1)}\left(z\right)\sim z^n/(2n+1)!!,$$

ⓘ

Symbols:

$\sim$: asymptotic equality, $!!$: double factorial, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, ${𝗃}_n\left(z\right)$: spherical Bessel function of the first kind, $n$: integer and $z$: complex variable

A&S Ref:

10.1.4

Permalink:

http://dlmf.nist.gov/10.52.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §10.52(i), §10.52 and Ch.10

►

10.52.2 $$-{𝗒}_n\left(z\right),\mathrm{i}{𝗁}_n^{(1)}\left(z\right),-\mathrm{i}{𝗁}_n^{(2)}\left(z\right),{(-1)}^n{𝗂}_n^{(2)}\left(z\right),(2/\pi ){𝗄}_n\left(z\right)\sim (2n-1)!!/z^{n+1}.$$

ⓘ

Symbols:

$\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $!!$: double factorial, $\mathrm{i}$: imaginary unit, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, ${𝗄}_n\left(z\right)$: modified spherical Bessel function, ${𝗒}_n\left(z\right)$: spherical Bessel function of the second kind, ${𝗁}_n^{(1)}\left(z\right)$: spherical Bessel function of the third kind, ${𝗁}_n^{(2)}\left(z\right)$: spherical Bessel function of the third kind, $n$: integer and $z$: complex variable

A&S Ref:

10.1.5

Permalink:

http://dlmf.nist.gov/10.52.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §10.52(i), §10.52 and Ch.10

… ►

10.52.5 $${𝗂}_n^{(1)}\left(z\right)\sim {𝗂}_n^{(2)}\left(z\right)\sim \frac{1}{2}{z}^{-1}{\mathrm{e}}^z,$$ ,

ⓘ

Symbols:

$\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{ph}$: phase, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, $n$: integer, $z$: complex variable and $\delta$: small positive constant

Permalink:

http://dlmf.nist.gov/10.52.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §10.52(ii), §10.52 and Ch.10

►

10.52.6 $${𝗄}_n\left(z\right)\sim \frac{1}{2}\pi z^{-1}{\mathrm{e}}^{-z}.$$

ⓘ

Symbols:

$\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, ${𝗄}_n\left(z\right)$: modified spherical Bessel function, $n$: integer and $z$: complex variable

Permalink:

http://dlmf.nist.gov/10.52.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §10.52(ii), §10.52 and Ch.10

3: 10.47 Definitions and Basic Properties

… ►

Equation (10.47.2)

… ► ${𝗂}_n^{(1)}\left(z\right)$, ${𝗂}_n^{(2)}\left(z\right)$, and ${𝗄}_n\left(z\right)$ are the modified spherical Bessel functions. … ►

10.47.11 $${𝗄}_n\left(z\right)={(-1)}^{n+1}\frac{1}{2}\pi \left({𝗂}_n^{(1)}\left(z\right)-{𝗂}_n^{(2)}\left(z\right)\right).$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, ${𝗄}_n\left(z\right)$: modified spherical Bessel function, $n$: integer and $z$: complex variable

A&S Ref:

10.2.4 (modified)

Referenced by:

§10.47(v), §10.53, §10.56, §10.57

Permalink:

http://dlmf.nist.gov/10.47.E11

Encodings:

pMML, png, TeX

See also:

Annotations for §10.47(iv), §10.47 and Ch.10

… ►

10.47.16 ${𝗂}_n^{(1)}\left(-z\right)={(-1)}^n{𝗂}_n^{(1)}\left(z\right),$ ${𝗂}_n^{(2)}\left(-z\right)={(-1)}^{n+1}{𝗂}_n^{(2)}\left(z\right),$

ⓘ

Symbols:

${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, $n$: integer and $z$: complex variable

Referenced by:

§10.47(v)

Permalink:

http://dlmf.nist.gov/10.47.E16

Encodings:

pMML, pMML, png, png, TeX, TeX

See also:

Annotations for §10.47(v), §10.47 and Ch.10

►

10.47.17 $${𝗄}_n\left(-z\right)=-\frac{1}{2}\pi \left({𝗂}_n^{(1)}\left(z\right)+{𝗂}_n^{(2)}\left(z\right)\right).$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, ${𝗄}_n\left(z\right)$: modified spherical Bessel function, $n$: integer and $z$: complex variable

Referenced by:

§10.47(v)

Permalink:

http://dlmf.nist.gov/10.47.E17

Encodings:

pMML, png, TeX

See also:

Annotations for §10.47(v), §10.47 and Ch.10

4: 10.56 Generating Functions

… ►

10.56.3 $$\frac{\cosh \sqrt{z^2+2\mathrm{i}zt}}{z}=\frac{\cosh z}{z}+\sum _{n=1}^{\mathrm{\infty }}\frac{{(\mathrm{i}t)}^n}{n!}{𝗂}_{n-1}^{(1)}\left(z\right),$$

ⓘ

Symbols:

$!$: factorial (as in $n!$), $\cosh z$: hyperbolic cosine function, $\mathrm{i}$: imaginary unit, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, $n$: integer and $z$: complex variable

Referenced by:

§10.56

Permalink:

http://dlmf.nist.gov/10.56.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §10.56 and Ch.10

►

10.56.4 $$\frac{\sinh \sqrt{z^2+2\mathrm{i}zt}}{z}=\frac{\sinh z}{z}+\sum _{n=1}^{\mathrm{\infty }}\frac{{(\mathrm{i}t)}^n}{n!}{𝗂}_{n-1}^{(2)}\left(z\right),$$

ⓘ

Symbols:

$!$: factorial (as in $n!$), $\sinh z$: hyperbolic sine function, $\mathrm{i}$: imaginary unit, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, $n$: integer and $z$: complex variable

Referenced by:

§10.56

Permalink:

http://dlmf.nist.gov/10.56.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §10.56 and Ch.10

►

10.56.5 $$\frac{\exp \left(-\sqrt{z^2+2\mathrm{i}zt}\right)}{z}=\frac{{\mathrm{e}}^{-z}}{z}+\frac{2}{\pi }\sum _{n=1}^{\mathrm{\infty }}\frac{{(-\mathrm{i}t)}^n}{n!}{𝗄}_{n-1}\left(z\right).$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\exp z$: exponential function, $\mathrm{e}$: base of natural logarithm, $!$: factorial (as in $n!$), $\mathrm{i}$: imaginary unit, ${𝗄}_n\left(z\right)$: modified spherical Bessel function, $n$: integer and $z$: complex variable

Referenced by:

§10.56, Ch.10

Permalink:

http://dlmf.nist.gov/10.56.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §10.56 and Ch.10

5: 10.1 Special Notation

… ►The main functions treated in this chapter are the Bessel functions $J_{\nu }\left(z\right)$, $Y_{\nu }\left(z\right)$; Hankel functions $H_{\nu }^{(1)}\left(z\right)$, $H_{\nu }^{(2)}\left(z\right)$; modified Bessel functions $I_{\nu }\left(z\right)$, $K_{\nu }\left(z\right)$; spherical Bessel functions ${𝗃}_n\left(z\right)$, ${𝗒}_n\left(z\right)$, ${𝗁}_n^{(1)}\left(z\right)$, ${𝗁}_n^{(2)}\left(z\right)$; modified spherical Bessel functions ${𝗂}_n^{(1)}\left(z\right)$, ${𝗂}_n^{(2)}\left(z\right)$, ${𝗄}_n\left(z\right)$; Kelvin functions ${\mathrm{ber}}_{\nu }\left(x\right)$, ${\mathrm{bei}}_{\nu }\left(x\right)$, ${\ker }_{\nu }\left(x\right)$, ${\mathrm{kei}}_{\nu }\left(x\right)$. For the spherical Bessel functions and modified spherical Bessel functions the order $n$ is a nonnegative integer. … ►For older notations see British Association for the Advancement of Science (1937, pp. xix–xx) and Watson (1944, Chapters 1–3).

6: 10.49 Explicit Formulas

… ►

§10.49(ii) Modified Functions

… ►

10.49.8 $${𝗂}_n^{(1)}\left(z\right)=\frac{1}{2}{\mathrm{e}}^z\sum _{k=0}^n{(-1)}^k\frac{a_k(n+\frac{1}{2})}{z^{k+1}}+{(-1)}^{n+1}\frac{1}{2}{\mathrm{e}}^{-z}\sum _{k=0}^n\frac{a_k(n+\frac{1}{2})}{z^{k+1}}.$$

ⓘ

Symbols:

$\mathrm{e}$: base of natural logarithm, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, $n$: integer, $k$: nonnegative integer, $z$: complex variable and $a_k(\nu )$: polynomial coefficient

A&S Ref:

10.2.9 (modified)

Referenced by:

§10.52(ii)

Permalink:

http://dlmf.nist.gov/10.49.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §10.49(ii), §10.49 and Ch.10

… ►

10.49.10 $${𝗂}_n^{(2)}\left(z\right)=\frac{1}{2}{\mathrm{e}}^z\sum _{k=0}^n{(-1)}^k\frac{a_k(n+\frac{1}{2})}{z^{k+1}}+{(-1)}^n\frac{1}{2}{\mathrm{e}}^{-z}\sum _{k=0}^n\frac{a_k(n+\frac{1}{2})}{z^{k+1}}.$$

ⓘ

Symbols:

$\mathrm{e}$: base of natural logarithm, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, $n$: integer, $k$: nonnegative integer, $z$: complex variable and $a_k(\nu )$: polynomial coefficient

A&S Ref:

10.2.10 (modified)

Referenced by:

§10.52(ii)

Permalink:

http://dlmf.nist.gov/10.49.E10

Encodings:

pMML, png, TeX

See also:

Annotations for §10.49(ii), §10.49 and Ch.10

… ►

10.49.12 $${𝗄}_n\left(z\right)=\frac{1}{2}\pi {\mathrm{e}}^{-z}\sum _{k=0}^n\frac{a_k(n+\frac{1}{2})}{z^{k+1}}.$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, ${𝗄}_n\left(z\right)$: modified spherical Bessel function, $n$: integer, $k$: nonnegative integer, $z$: complex variable and $a_k(\nu )$: polynomial coefficient

A&S Ref:

10.2.15

Referenced by:

§10.52(ii)

Permalink:

http://dlmf.nist.gov/10.49.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §10.49(ii), §10.49 and Ch.10

… ►

10.49.20 $${\left({𝗂}_n^{(1)}\left(z\right)\right)}^2-{\left({𝗂}_n^{(2)}\left(z\right)\right)}^2={(-1)}^{n+1}\sum _{k=0}^n{(-1)}^k\frac{s_k(n+\frac{1}{2})}{z^{2k+2}}.$$

ⓘ

Symbols:

${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, $n$: integer, $k$: nonnegative integer, $z$: complex variable and $s_k(n)$

A&S Ref:

10.2.26

Referenced by:

§10.49(iv)

Permalink:

http://dlmf.nist.gov/10.49.E20

Encodings:

pMML, png, TeX

See also:

Annotations for §10.49(iv), §10.49 and Ch.10

…

7: 6.10 Other Series Expansions

… ►

§6.10(ii) Expansions in Series of Spherical Bessel Functions

… ►

6.10.6 $$\mathrm{Ei}\left(x\right)=\gamma +\ln \left|x\right|+\sum _{n=0}^{\mathrm{\infty }}{(-1)}^n(x-a_n){\left({𝗂}_n^{(1)}\left(\frac{1}{2}x\right)\right)}^2,$$ $x\ne 0$,

ⓘ

Symbols:

$\gamma$: Euler’s constant, $\mathrm{Ei}\left(x\right)$: exponential integral, $\ln z$: principal branch of logarithm function, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, $x$: real variable, $n$: nonnegative integer and $a_n$: coefficients

Referenced by:

§6.18(i)

Permalink:

http://dlmf.nist.gov/6.10.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §6.10(ii), §6.10 and Ch.6

… ►

6.10.8 $$\mathrm{Ein}\left(z\right)=z{\mathrm{e}}^{-z/2}\left({𝗂}_0^{(1)}\left(\frac{1}{2}z\right)+\sum _{n=1}^{\mathrm{\infty }}\frac{2n+1}{n(n+1)}{𝗂}_n^{(1)}\left(\frac{1}{2}z\right)\right).$$

ⓘ

Symbols:

$\mathrm{Ein}\left(z\right)$: complementary exponential integral, $\mathrm{e}$: base of natural logarithm, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, $z$: complex variable and $n$: nonnegative integer

Referenced by:

§6.10(ii)

Permalink:

http://dlmf.nist.gov/6.10.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §6.10(ii), §6.10 and Ch.6

…

8: 10.53 Power Series

… ►

10.53.3 $${𝗂}_n^{(1)}\left(z\right)=z^n\sum _{k=0}^{\mathrm{\infty }}\frac{{(\frac{1}{2}{z}^2)}^k}{k!(2n+2k+1)!!},$$

ⓘ

Symbols:

$!!$: double factorial, $!$: factorial (as in $n!$), ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, $n$: integer, $k$: nonnegative integer and $z$: complex variable

A&S Ref:

10.2.5

Referenced by:

§10.53

Permalink:

http://dlmf.nist.gov/10.53.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §10.53 and Ch.10

►

10.53.4 $${𝗂}_n^{(2)}\left(z\right)=\frac{{(-1)}^n}{z^{n+1}}\sum _{k=0}^n\frac{(2n-2k-1)!!{(-\frac{1}{2}{z}^2)}^k}{k!}+\frac{1}{z^{n+1}}\sum _{k=n+1}^{\mathrm{\infty }}\frac{{(\frac{1}{2}{z}^2)}^k}{k!(2k-2n-1)!!}.$$

ⓘ

Symbols:

$!!$: double factorial, $!$: factorial (as in $n!$), ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, $n$: integer, $k$: nonnegative integer and $z$: complex variable

A&S Ref:

10.2.6

Referenced by:

§10.53

Permalink:

http://dlmf.nist.gov/10.53.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §10.53 and Ch.10

…

9: 10.50 Wronskians and Cross-Products

… ►

10.50.4 $${𝗃}_0\left(z\right){𝗃}_n\left(z\right)+{𝗒}_0\left(z\right){𝗒}_n\left(z\right)=\cos \left(\frac{1}{2}n\pi \right)\sum _{k=0}^{\lfloor n/2\rfloor }{(-1)}^k\frac{a_{2k}(n+\frac{1}{2})}{z^{2k+2}}+\sin \left(\frac{1}{2}n\pi \right)\sum _{k=0}^{\lfloor (n-1)/2\rfloor }{(-1)}^k\frac{a_{2k+1}(n+\frac{1}{2})}{z^{2k+3}},$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\lfloor x\rfloor$: floor of $x$ , $\sin z$: sine function, ${𝗃}_n\left(z\right)$: spherical Bessel function of the first kind, ${𝗒}_n\left(z\right)$: spherical Bessel function of the second kind, $n$: integer, $k$: nonnegative integer, $z$: complex variable and $a_k(\nu )$: polynomial coefficient

A&S Ref:

10.1.33 (modified)

Referenced by:

§10.50, §10.50

Permalink:

http://dlmf.nist.gov/10.50.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §10.50 and Ch.10

…

10: 10.60 Sums

… ►

10.60.3 $$\frac{{\mathrm{e}}^{-w}}{w}=\frac{2}{\pi }\sum _{n=0}^{\mathrm{\infty }}(2n+1){𝗂}_n^{(1)}\left(v\right){𝗄}_n\left(u\right)P_n\left(\cos \alpha \right),$$ .

ⓘ

Symbols:

$P_n\left(x\right)$: Legendre polynomial, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, ${𝗄}_n\left(z\right)$: modified spherical Bessel function and $n$: integer

A&S Ref:

10.2.35 (with condition added)

Referenced by:

§10.60(i)

Permalink:

http://dlmf.nist.gov/10.60.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §10.60(i), §10.60 and Ch.10

… ►

10.60.6 $${𝗄}_n\left(2z\right)=\frac{1}{\pi }n!z^{n+1}\sum _{k=0}^n{(-1)}^k\frac{2n-2k+1}{k!(2n-k+1)!}{𝗄}_{n-k}^2\left(z\right).$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $!$: factorial (as in $n!$), ${𝗄}_n\left(z\right)$: modified spherical Bessel function, $n$: integer, $k$: nonnegative integer and $z$: complex variable

A&S Ref:

10.2.38

Referenced by:

§10.60(ii), Ch.10

Permalink:

http://dlmf.nist.gov/10.60.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §10.60(ii), §10.60 and Ch.10

… ►

10.60.8 $${\mathrm{e}}^{z\cos \alpha }=\sum _{n=0}^{\mathrm{\infty }}(2n+1){𝗂}_n^{(1)}\left(z\right)P_n\left(\cos \alpha \right),$$

ⓘ

Symbols:

$P_n\left(x\right)$: Legendre polynomial, $\cos z$: cosine function, $\mathrm{e}$: base of natural logarithm, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, $n$: integer and $z$: complex variable

A&S Ref:

10.2.36

Permalink:

http://dlmf.nist.gov/10.60.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §10.60(iii), §10.60 and Ch.10

►

10.60.9 $${\mathrm{e}}^{-z\cos \alpha }=\sum _{n=0}^{\mathrm{\infty }}{(-1)}^n(2n+1){𝗂}_n^{(1)}\left(z\right)P_n\left(\cos \alpha \right).$$

ⓘ

Symbols:

$P_n\left(x\right)$: Legendre polynomial, $\cos z$: cosine function, $\mathrm{e}$: base of natural logarithm, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, $n$: integer and $z$: complex variable

A&S Ref:

10.2.37

Referenced by:

§10.60(iii), Ch.10

Permalink:

http://dlmf.nist.gov/10.60.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §10.60(iii), §10.60 and Ch.10

… ►For further sums of series of spherical Bessel functions, or modified spherical Bessel functions, see §6.10(ii), Luke (1969b, pp. 55–58), Vavreck and Thompson (1984), Harris (2000), and Rottbrand (2000). …