modified

SearchAdvancedHelp

(0.001 seconds)

1—10 of 177 matching pages

1: 28.20 Definitions and Basic Properties

… ►

§28.20(i) Modified Mathieu’s Equation

… ►

28.20.1 $$w^{\prime \prime }-\left(a-2q\cosh \left(2z\right)\right)w=0,$$

ⓘ

Symbols:

$\cosh z$: hyperbolic cosine function, $q=h^2$: parameter, $z$: complex variable, $a$: parameter and $w(z)$: Mathieu’s equation solution

A&S Ref:

20.1.2 (in slightly different form) 20.8.6

Referenced by:

§28.20(iii), §28.32(i), 1st item, 2nd item, item (b), §28.8(iv), §28.8(iv)

Permalink:

http://dlmf.nist.gov/28.20.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §28.20(i), §28.20 and Ch.28

… ►

§28.20(ii) Solutions ${\mathrm{Ce}}_{\nu }$, ${\mathrm{Se}}_{\nu }$, ${\mathrm{Me}}_{\nu }$, ${\mathrm{Fe}}_n$, ${\mathrm{Ge}}_n$

… ►

§28.20(iv) Radial Mathieu Functions ${\mathrm{Mc}}_n^{(j)}$, ${\mathrm{Ms}}_n^{(j)}$

… ►

§28.20(vi) Wronskians

…

2: 28.21 Graphics

§28.21 Graphics

… ►

►

►

Figure 28.21.1: ${\mathrm{Mc}}_0^{(1)}(x,h)$ for $0\le h\le 3$, $0\le x\le 2$. Magnify 3D Help

►

►

►

Figure 28.21.2: ${\mathrm{Mc}}_1^{(1)}(x,h)$ for $0\le h\le 3$, $0\le x\le 2$. Magnify 3D Help

►

►

►

Figure 28.21.3: ${\mathrm{Mc}}_0^{(2)}(x,h)$ for $0.1\le h\le 2$, $0\le x\le 2$. Magnify 3D Help

… ►

►

►

Figure 28.21.6: ${\mathrm{Ms}}_1^{(2)}(x,h)$ for $0.2\le h\le 2$, $0\le x\le 2$. Magnify 3D Help

3: 10.26 Graphics

… ►

§10.26(i) Real Order and Variable

… ►

►►

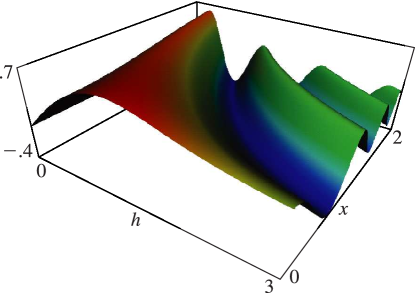
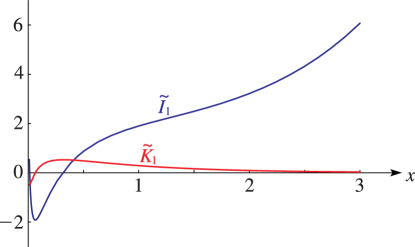
Figure 10.26.7: ${\tilde{I}}_{1/2}\left(x\right)$, ${\tilde{K}}_{1/2}\left(x\right)$, $0.01\le x\le 3$. Magnify

►

►►

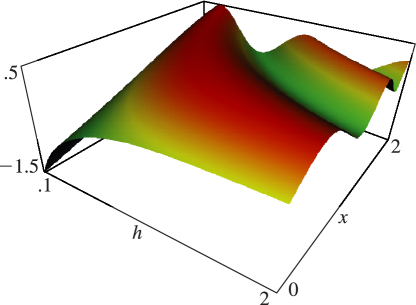
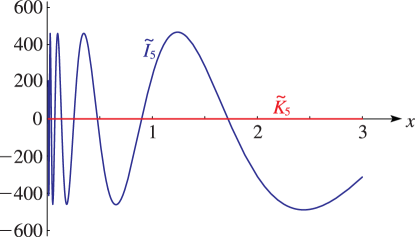
Figure 10.26.8: ${\tilde{I}}_1\left(x\right)$, ${\tilde{K}}_1\left(x\right)$, $0.01\le x\le 3$. Magnify

►

►►

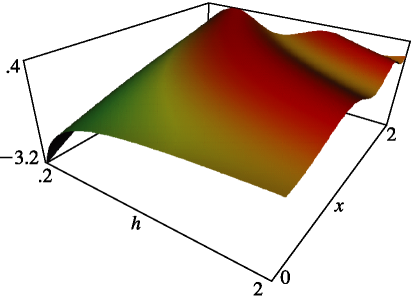
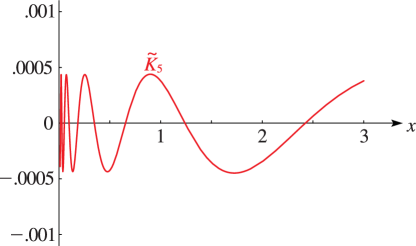
Figure 10.26.9: ${\tilde{I}}_5\left(x\right)$, ${\tilde{K}}_5\left(x\right)$, $0.01\le x\le 3$. Magnify

►

►►

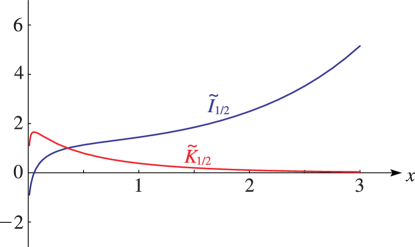
Figure 10.26.10: ${\tilde{K}}_5\left(x\right)$, $0.01\le x\le 3$. Magnify

4: 10.29 Recurrence Relations and Derivatives

… ►

§10.29(i) Recurrence Relations

►With ${𝒵}_{\nu }\left(z\right)$ defined as in §10.25(ii), … ►

$I_0^{\prime }\left(z\right)=I_1\left(z\right),$

… ►For results on modified quotients of the form $z{𝒵}_{\nu \pm 1}\left(z\right)/{𝒵}_{\nu }\left(z\right)$ see Onoe (1955) and Onoe (1956). ►

§10.29(ii) Derivatives

…

5: 28.27 Addition Theorems

§28.27 Addition Theorems

… ►They are analogous to the addition theorems for Bessel functions (§10.23(ii)) and modified Bessel functions (§10.44(ii)). …

6: 10.28 Wronskians and Cross-Products

§10.28 Wronskians and Cross-Products

►

10.28.1 $$𝒲\left\{I_{\nu }\left(z\right),I_{-\nu }\left(z\right)\right\}=I_{\nu }\left(z\right)I_{-\nu -1}\left(z\right)-I_{\nu +1}\left(z\right)I_{-\nu }\left(z\right)=-2\sin \left(\nu \pi \right)/(\pi z),$$

ⓘ

Symbols:

$𝒲$: Wronskian, $\pi$: the ratio of the circumference of a circle to its diameter, $I_{\nu }\left(z\right)$: modified Bessel function of the first kind, $\sin z$: sine function, $z$: complex variable and $\nu$: complex parameter

A&S Ref:

9.6.14

Permalink:

http://dlmf.nist.gov/10.28.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §10.28 and Ch.10

►

10.28.2 $$𝒲\left\{K_{\nu }\left(z\right),I_{\nu }\left(z\right)\right\}=I_{\nu }\left(z\right)K_{\nu +1}\left(z\right)+I_{\nu +1}\left(z\right)K_{\nu }\left(z\right)=1/z.$$

ⓘ

Symbols:

$𝒲$: Wronskian, $I_{\nu }\left(z\right)$: modified Bessel function of the first kind, $K_{\nu }\left(z\right)$: modified Bessel function of the second kind, $z$: complex variable and $\nu$: complex parameter

A&S Ref:

9.6.15

Permalink:

http://dlmf.nist.gov/10.28.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §10.28 and Ch.10

7: 10.44 Sums

… ►

§10.44(i) Multiplication Theorem

… ►

§10.44(ii) Addition Theorems

… ►

Graf’s and Gegenbauer’s Addition Theorems

… ►

§10.44(iii) Neumann-Type Expansions

… ►

§10.44(iv) Compendia

…

8: 28.1 Special Notation

… ►and the modified Mathieu functions ► ►►►

${\mathrm{Ce}}_{\nu }(z,q)$,	${\mathrm{Se}}_{\nu }(z,q)$,	${\mathrm{Fe}}_n(z,q)$,	${\mathrm{Ge}}_n(z,q)$,
${\mathrm{Me}}_{\nu }(z,q)$,	${\mathrm{M}}_{\nu }^{(j)}(z,h)$,	${\mathrm{Mc}}_n^{(j)}(z,h)$,	${\mathrm{Ms}}_n^{(j)}(z,h)$,
…

►The functions ${\mathrm{Mc}}_n^{(j)}(z,h)$ and ${\mathrm{Ms}}_n^{(j)}(z,h)$ are also known as the radial Mathieu functions. … ►The radial functions ${\mathrm{Mc}}_n^{(j)}(z,h)$ and ${\mathrm{Ms}}_n^{(j)}(z,h)$ are denoted by ${\mathrm{Mc}}_n^{(j)}(z,q)$ and ${\mathrm{Ms}}_n^{(j)}(z,q)$, respectively.

9: 10.45 Functions of Imaginary Order

§10.45 Functions of Imaginary Order

… ►and ${\tilde{I}}_{\nu }\left(x\right)$, ${\tilde{K}}_{\nu }\left(x\right)$ are real and linearly independent solutions of (10.45.1): … ►The corresponding result for ${\tilde{K}}_{\nu }\left(x\right)$ is given by … ► … ►

10: 10.35 Generating Function and Associated Series

§10.35 Generating Function and Associated Series

… ►

10.35.4 $$1=I_0\left(z\right)-2I_2\left(z\right)+2I_4\left(z\right)-2I_6\left(z\right)+\mathrm{\cdots },$$

ⓘ

Symbols:

$I_{\nu }\left(z\right)$: modified Bessel function of the first kind and $z$: complex variable

A&S Ref:

9.6.36

Permalink:

http://dlmf.nist.gov/10.35.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §10.35 and Ch.10

►

10.35.5 $${\mathrm{e}}^{\pm z}=I_0\left(z\right)\pm 2I_1\left(z\right)+2I_2\left(z\right)\pm 2I_3\left(z\right)+\mathrm{\cdots },$$

ⓘ

Symbols:

$\mathrm{e}$: base of natural logarithm, $I_{\nu }\left(z\right)$: modified Bessel function of the first kind and $z$: complex variable

A&S Ref:

9.6.37,9.6.38

Permalink:

http://dlmf.nist.gov/10.35.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §10.35 and Ch.10

►

$$\cosh z=I_0\left(z\right)+2I_2\left(z\right)+2I_4\left(z\right)+2I_6\left(z\right)+\mathrm{\dots },$$

►

$$\sinh z=2I_1\left(z\right)+2I_3\left(z\right)+2I_5\left(z\right)+\mathrm{\dots }.$$