imaginary part

SearchAdvancedHelp

(0.005 seconds)

1—10 of 188 matching pages

1: 19.3 Graphics

… ►

►

►

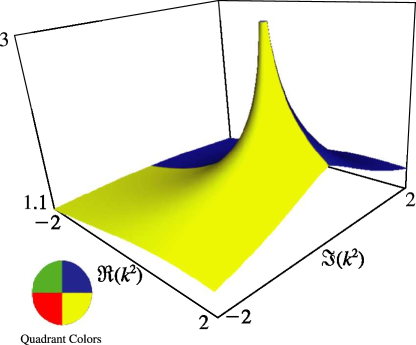
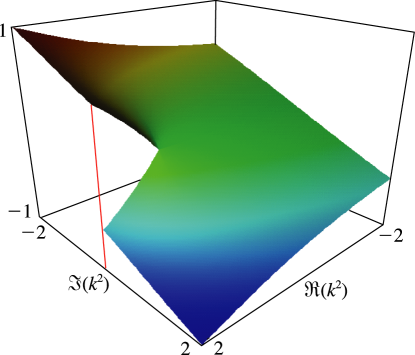
Figure 19.3.7: $K\left(k\right)$ as a function of complex $k^2$ for $-2\le \mathrm{\Re }\left(k^2\right)\le 2$, $-2\le \mathrm{\Im }\left(k^2\right)\le 2$. … Magnify 3D Help

►

►

►

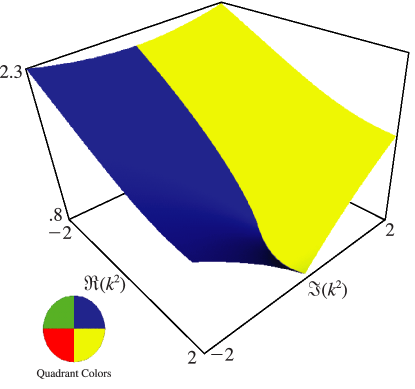
Figure 19.3.8: $E\left(k\right)$ as a function of complex $k^2$ for $-2\le \mathrm{\Re }\left(k^2\right)\le 2$, $-2\le \mathrm{\Im }\left(k^2\right)\le 2$. … Magnify 3D Help

►

►

►

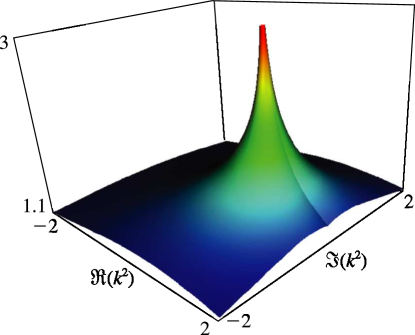
Figure 19.3.9: $\mathrm{\Re }\left(K\left(k\right)\right)$ as a function of complex $k^2$ for $-2\le \mathrm{\Re }\left(k^2\right)\le 2$, $-2\le \mathrm{\Im }\left(k^2\right)\le 2$. … Magnify 3D Help

►

►

►

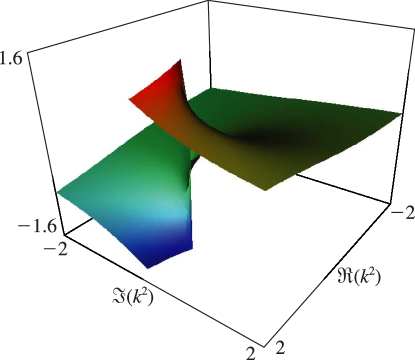
Figure 19.3.10: $\mathrm{\Im }\left(K\left(k\right)\right)$ as a function of complex $k^2$ for $-2\le \mathrm{\Re }\left(k^2\right)\le 2$, $-2\le \mathrm{\Im }\left(k^2\right)\le 2$. … Magnify 3D Help

… ►

►

►

Figure 19.3.12: $\mathrm{\Im }\left(E\left(k\right)\right)$ as a function of complex $k^2$ for $-2\le \mathrm{\Re }\left(k^2\right)\le 2$, $-2\le \mathrm{\Im }\left(k^2\right)\le 2$. … Magnify 3D Help

2: 29.16 Asymptotic Expansions

… ►The approximations for Lamé polynomials hold uniformly on the rectangle $0\le \mathrm{\Re }z\le K$, $0\le \mathrm{\Im }z\le K^{\prime }$, when $nk$ and $n{k}^{\prime }$ assume large real values. …

3: 7.9 Continued Fractions

… ►

7.9.3 $$w\left(z\right)=\frac{\mathrm{i}}{\sqrt{\pi }}\frac{1}{z-}\frac{\frac{1}{2}}{z-}\frac{1}{z-}\frac{\frac{3}{2}}{z-}\frac{2}{z-}\mathrm{\cdots },$$ $\mathrm{\Im }z>0$.

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $w\left(z\right)$: Faddeeva (or Faddeyeva) function, $\mathrm{\Im }$: imaginary part, $\mathrm{i}$: imaginary unit and $z$: complex variable

A&S Ref:

7.1.15 (in different form)

Permalink:

http://dlmf.nist.gov/7.9.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §7.9 and Ch.7

…

4: 28.25 Asymptotic Expansions for Large $\mathrm{\Re }z$

… ►

28.25.4 $$\mathrm{\Re }z\to +\mathrm{\infty },$$ $-\pi +\delta \le \mathrm{ph}h+\mathrm{\Im }z\le 2\pi -\delta$,

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{\Im }$: imaginary part, $\mathrm{ph}$: phase, $\mathrm{\Re }$: real part, $h$: parameter, $z$: complex variable and $\delta$: arbitrary small positive constant

Permalink:

http://dlmf.nist.gov/28.25.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §28.25 and Ch.28

… ►

28.25.5 $$\mathrm{\Re }z\to +\mathrm{\infty },$$ $-2\pi +\delta \le \mathrm{ph}h+\mathrm{\Im }z\le \pi -\delta$,

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{\Im }$: imaginary part, $\mathrm{ph}$: phase, $\mathrm{\Re }$: real part, $h$: parameter, $z$: complex variable and $\delta$: arbitrary small positive constant

Permalink:

http://dlmf.nist.gov/28.25.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §28.25 and Ch.28

…

5: 19.32 Conformal Map onto a Rectangle

… ►

19.32.2 $$dz=-\frac{1}{2}\left(\prod _{j=1}^3{(p-x_j)}^{-1/2}\right)dp,$$ $\mathrm{\Im }p>0$; , $j=1,2,3$.

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{\Im }$: imaginary part, $\mathrm{ph}$: phase and $z(p)$: function

Referenced by:

§19.32

Permalink:

http://dlmf.nist.gov/19.32.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §19.32 and Ch.19

…

6: 23.1 Special Notation

… ► ►►►►►

$𝕃$	lattice in $ℂ$.
…
$z=x+\mathrm{i}y$	complex variable, except in §§23.20(ii), 23.21(iii).
…
$2{\omega }_1,2{\omega }_3$	lattice generators ($\mathrm{\Im }\left({\omega }_3/{\omega }_1\right)>0$).
…
$\tau ={\omega }_3/{\omega }_1$	lattice parameter ($\mathrm{\Im }\tau >0$).
…

… ►Whittaker and Watson (1927) requires only $\mathrm{\Im }\left({\omega }_3/{\omega }_1\right)\ne 0$, instead of $\mathrm{\Im }\left({\omega }_3/{\omega }_1\right)>0$. …

7: 27.14 Unrestricted Partitions

… ►

27.14.12 $$\eta \left(\tau \right)={\mathrm{e}}^{\pi \mathrm{i}\tau /12}\prod _{n=1}^{\mathrm{\infty }}(1-{\mathrm{e}}^{2\pi \mathrm{i}n\tau }),$$ $\mathrm{\Im }\tau >0$.

ⓘ

Defines:

$\eta \left(\tau \right)$: Dedekind’s eta function (or Dedekind modular function)

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{\Im }$: imaginary part, $\mathrm{i}$: imaginary unit and $n$: positive integer

Referenced by:

§23.15(ii), §27.14(vi)

Permalink:

http://dlmf.nist.gov/27.14.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §27.14(iv), §27.14 and Ch.27

… ►

27.14.13 $$\eta \left(\tau \right)={\mathrm{e}}^{\pi \mathrm{i}\tau /12}f\left({\mathrm{e}}^{2\pi \mathrm{i}\tau }\right).$$

ⓘ

Symbols:

$\eta \left(\tau \right)$: Dedekind’s eta function (or Dedekind modular function), $f\left(x\right)$: Euler’s reciprocal function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{\Im }$: imaginary part and $\mathrm{i}$: imaginary unit

Permalink:

http://dlmf.nist.gov/27.14.E13

Encodings:

pMML, png, TeX

See also:

Annotations for §27.14(iv), §27.14 and Ch.27

… ►

27.14.14 $$\eta \left(\frac{a\tau +b}{c\tau +d}\right)=\epsilon {(-\mathrm{i}(c\tau +d))}^{\frac{1}{2}}\eta \left(\tau \right),$$

ⓘ

Symbols:

$\eta \left(\tau \right)$: Dedekind’s eta function (or Dedekind modular function), $\mathrm{\Im }$: imaginary part, $\mathrm{i}$: imaginary unit, $a$: integer, $b$: integer, $c$: integer and $d$: integer

Referenced by:

§17.2(i)

Permalink:

http://dlmf.nist.gov/27.14.E14

Encodings:

pMML, png, TeX

See also:

Annotations for §27.14(iv), §27.14 and Ch.27

… ►

27.14.16 $$\mathrm{\Delta }\left(\tau \right)={(2\pi )}^{12}{(\eta \left(\tau \right))}^{24},$$ $\mathrm{\Im }\tau >0$,

ⓘ

Defines:

$\mathrm{\Delta }\left(\tau \right)$: discriminant function

Symbols:

$\eta \left(\tau \right)$: Dedekind’s eta function (or Dedekind modular function), $\pi$: the ratio of the circumference of a circle to its diameter and $\mathrm{\Im }$: imaginary part

Permalink:

http://dlmf.nist.gov/27.14.E16

Encodings:

pMML, png, TeX

See also:

Annotations for §27.14(vi), §27.14 and Ch.27

… ►

27.14.17 $$\mathrm{\Delta }\left(\frac{a\tau +b}{c\tau +d}\right)={(c\tau +d)}^{12}\mathrm{\Delta }\left(\tau \right),$$

ⓘ

Symbols:

$\mathrm{\Delta }\left(\tau \right)$: discriminant function and $\mathrm{\Im }$: imaginary part

Permalink:

http://dlmf.nist.gov/27.14.E17

Encodings:

pMML, png, TeX

See also:

Annotations for §27.14(vi), §27.14 and Ch.27

…

8: 20.14 Methods of Computation

… ►For values of $\left|q\right|$ near $1$ the transformations of §20.7(viii) can be used to replace $\tau$ with a value that has a larger imaginary part and hence a smaller value of $\left|q\right|$. …In theory, starting from any value of $\tau$, a finite number of applications of the transformations $\tau \to \tau +1$ and $\tau \to -1/\tau$ will result in a value of $\tau$ with $\mathrm{\Im }\tau \ge \sqrt{3}/2$; see §23.18. In practice a value with, say, $\mathrm{\Im }\tau \ge 1/2$, $\left|q\right|\le 0.2$, is found quickly and is satisfactory for numerical evaluation.

9: 23.11 Integral Representations

… ►provided that and .

10: 5.4 Special Values and Extrema

… ►

5.4.16 $$\mathrm{\Im }\psi \left(\mathrm{i}y\right)=\frac{1}{2y}+\frac{\pi }{2}\coth \left(\pi y\right),$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\psi \left(z\right)$: psi (or digamma) function, $\coth z$: hyperbolic cotangent function, $\mathrm{\Im }$: imaginary part, $\mathrm{i}$: imaginary unit and $y$: real variable

A&S Ref:

6.3.11

Permalink:

http://dlmf.nist.gov/5.4.E16

Encodings:

pMML, png, TeX

See also:

Annotations for §5.4(ii), §5.4 and Ch.5

►

5.4.17 $$\mathrm{\Im }\psi \left(\frac{1}{2}+\mathrm{i}y\right)=\frac{\pi }{2}\tanh \left(\pi y\right),$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\psi \left(z\right)$: psi (or digamma) function, $\tanh z$: hyperbolic tangent function, $\mathrm{\Im }$: imaginary part, $\mathrm{i}$: imaginary unit and $y$: real variable

A&S Ref:

6.3.12

Permalink:

http://dlmf.nist.gov/5.4.E17

Encodings:

pMML, png, TeX

See also:

Annotations for §5.4(ii), §5.4 and Ch.5

►

5.4.18 $$\mathrm{\Im }\psi \left(1+\mathrm{i}y\right)=-\frac{1}{2y}+\frac{\pi }{2}\coth \left(\pi y\right).$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\psi \left(z\right)$: psi (or digamma) function, $\coth z$: hyperbolic cotangent function, $\mathrm{\Im }$: imaginary part, $\mathrm{i}$: imaginary unit and $y$: real variable

A&S Ref:

6.3.13

Referenced by:

§5.4(ii)

Permalink:

http://dlmf.nist.gov/5.4.E18

Encodings:

pMML, png, TeX

See also:

Annotations for §5.4(ii), §5.4 and Ch.5

…