hyperbolic%20umbilic%20catastrophe

SearchAdvancedHelp

(0.003 seconds)

1—10 of 230 matching pages

1: 4.37 Inverse Hyperbolic Functions

§4.37 Inverse Hyperbolic Functions

… ►The principal values of the inverse hyperbolic cosecant, hyperbolic secant, and hyperbolic tangent are given by … ►

Inverse Hyperbolic Sine

… ►

Inverse Hyperbolic Cosine

… ►

Inverse Hyperbolic Tangent

…

2: 36.2 Catastrophes and Canonical Integrals

… ►

Normal Forms Associated with Canonical Integrals: Cuspoid Catastrophe with Codimension $K$

… ►

Normal Forms for Umbilic Catastrophes with Codimension $K=3$

… ►(hyperbolic umbilic). ►

Canonical Integrals

… ►

Diffraction Catastrophes

…

3: 36.4 Bifurcation Sets

… ►

Critical Points for Umbilics

… ►

Bifurcation (Catastrophe) Set for Umbilics

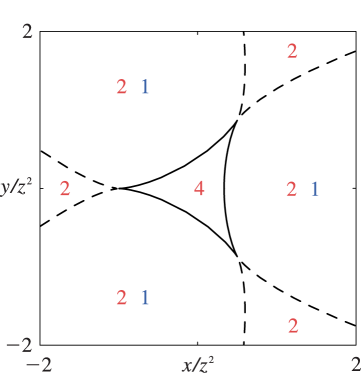
… ►Hyperbolic umbilic bifurcation set (codimension three): … ►Hyperbolic umbilic cusp line (rib): … ►

§36.4(ii) Visualizations

…

4: 36.5 Stokes Sets

… ►Stokes sets are surfaces (codimension one) in $𝐱$ space, across which ${\mathrm{\Psi }}_K(𝐱;k)$ or ${\mathrm{\Psi }}^{(\mathrm{U})}(𝐱;k)$ acquires an exponentially-small asymptotic contribution (in $k$), associated with a complex critical point of ${\mathrm{\Phi }}_K$ or . … ►

§36.5(iii) Umbilics

►

Elliptic Umbilic Stokes Set (Codimension three)

… ►

Hyperbolic Umbilic Stokes Set (Codimension three)

… ►

►►

Figure 36.5.5: Elliptic umbilic catastrophe with $z=\mathrm{constant}$. … Magnify

…

5: 36.1 Special Notation

§36.1 Special Notation

… ►The main functions covered in this chapter are cuspoid catastrophes ${\mathrm{\Phi }}_K(t;𝐱)$; umbilic catastrophes with codimension three ${\mathrm{\Phi }}^{(\mathrm{E})}(s,t;𝐱)$, ${\mathrm{\Phi }}^{(\mathrm{H})}(s,t;𝐱)$; canonical integrals ${\mathrm{\Psi }}_K\left(𝐱\right)$, ${\mathrm{\Psi }}^{(\mathrm{E})}\left(𝐱\right)$, ${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$; diffraction catastrophes ${\mathrm{\Psi }}_K(𝐱;k)$, ${\mathrm{\Psi }}^{(\mathrm{E})}(𝐱;k)$, ${\mathrm{\Psi }}^{(\mathrm{H})}(𝐱;k)$ generated by the catastrophes. …

6: 36.10 Differential Equations

… ►In terms of the normal forms (36.2.2) and (36.2.3), the ${\mathrm{\Psi }}^{(\mathrm{U})}\left(𝐱\right)$ satisfy the following operator equations … ►

36.10.14 $$3\left(\frac{{\partial }^2{\mathrm{\Psi }}^{(\mathrm{E})}}{{\partial x}^2}-\frac{{\partial }^2{\mathrm{\Psi }}^{(\mathrm{E})}}{{\partial y}^2}\right)+2\mathrm{i}z\frac{\partial {\mathrm{\Psi }}^{(\mathrm{E})}}{\partial x}-x{\mathrm{\Psi }}^{(\mathrm{E})}=0.$$

ⓘ

Symbols:

${\mathrm{\Psi }}^{(\mathrm{E})}\left(𝐱\right)$: elliptic umbilic canonical integral function, ${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$: hyperbolic umbilic canonical integral function, $\mathrm{i}$: imaginary unit, $\frac{\partial f}{\partial x}$: partial derivative of $f$ with respect to $x$ , $\partial x$: partial differential of $x$ , $y$: real parameter, $z$: real parameter and $x$: real parameter

Referenced by:

Erratum (V1.0.1) for Equation (36.10.14)

Permalink:

http://dlmf.nist.gov/36.10.E14

Encodings:

pMML, png, TeX

Errata (effective with 1.0.1):

Originally appeared with $\frac{\partial {\mathrm{\Psi }}^{(\mathrm{H})}}{\partial x}$, rather than $\frac{\partial {\mathrm{\Psi }}^{(\mathrm{E})}}{\partial x}$:

$$3\left(\frac{{\partial }^2{\mathrm{\Psi }}^{(\mathrm{E})}}{{\partial x}^2}-\frac{{\partial }^2{\mathrm{\Psi }}^{(\mathrm{E})}}{{\partial y}^2}\right)+2\mathrm{i}z\frac{\partial {\mathrm{\Psi }}^{(\mathrm{H})}}{\partial x}-x{\mathrm{\Psi }}^{(\mathrm{E})}=0.$$

See also:

Annotations for §36.10(iii), §36.10 and Ch.36

►

36.10.15 $$3\frac{{\partial }^2{\mathrm{\Psi }}^{(\mathrm{H})}}{{\partial x}^2}+\mathrm{i}z\frac{\partial {\mathrm{\Psi }}^{(\mathrm{H})}}{\partial y}-x{\mathrm{\Psi }}^{(\mathrm{H})}=0,$$

ⓘ

Symbols:

${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$: hyperbolic umbilic canonical integral function, $\mathrm{i}$: imaginary unit, $\frac{\partial f}{\partial x}$: partial derivative of $f$ with respect to $x$ , $\partial x$: partial differential of $x$ , $y$: real parameter, $z$: real parameter and $x$: real parameter

Permalink:

http://dlmf.nist.gov/36.10.E15

Encodings:

pMML, png, TeX

See also:

Annotations for §36.10(iii), §36.10 and Ch.36

►

36.10.16 $$3\frac{{\partial }^2{\mathrm{\Psi }}^{(\mathrm{H})}}{{\partial y}^2}+\mathrm{i}z\frac{\partial {\mathrm{\Psi }}^{(\mathrm{H})}}{\partial x}-y{\mathrm{\Psi }}^{(\mathrm{H})}=0.$$

ⓘ

Symbols:

${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$: hyperbolic umbilic canonical integral function, $\mathrm{i}$: imaginary unit, $\frac{\partial f}{\partial x}$: partial derivative of $f$ with respect to $x$ , $\partial x$: partial differential of $x$ , $y$: real parameter, $z$: real parameter and $x$: real parameter

Permalink:

http://dlmf.nist.gov/36.10.E16

Encodings:

pMML, png, TeX

See also:

Annotations for §36.10(iii), §36.10 and Ch.36

… ►

36.10.18 $$\mathrm{i}\frac{\partial {\mathrm{\Psi }}^{(\mathrm{H})}}{\partial z}=\frac{{\partial }^2{\mathrm{\Psi }}^{(\mathrm{H})}}{\partial x\partial y}.$$

ⓘ

Symbols:

${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$: hyperbolic umbilic canonical integral function, $\mathrm{i}$: imaginary unit, $\frac{\partial f}{\partial x}$: partial derivative of $f$ with respect to $x$ , $\partial x$: partial differential of $x$ , $y$: real parameter, $z$: real parameter and $x$: real parameter

Permalink:

http://dlmf.nist.gov/36.10.E18

Encodings:

pMML, png, TeX

See also:

Annotations for §36.10(iv), §36.10 and Ch.36

…

7: 36.3 Visualizations of Canonical Integrals

… ►

…

Figure 36.3.9: Modulus of hyperbolic umbilic canonical integral function $|{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,0\right)|$.

►

…

Figure 36.3.10: Modulus of hyperbolic umbilic canonical integral function $|{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,1\right)|$.

►

…

Figure 36.3.11: Modulus of hyperbolic umbilic canonical integral function $|{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,2\right)|$.

►

…

Figure 36.3.12: Modulus of hyperbolic umbilic canonical integral function $|{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,3\right)|$.

… ►

…

Figure 36.3.18: Phase of hyperbolic umbilic canonical integral $\mathrm{ph}{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,0\right)$.

…

8: 36.6 Scaling Relations

§36.6 Scaling Relations

►

Diffraction Catastrophe Scaling

… ►

${\mathrm{\Psi }}^{(\mathrm{U})}(𝐱;k)=k^{{\beta }^{(\mathrm{U})}}{\mathrm{\Psi }}^{(\mathrm{U})}\left({𝐲}^{(\mathrm{U})}(k)\right),$

… ►

Indices for $k$-Scaling of Magnitude of ${\mathrm{\Psi }}_K$ or ${\mathrm{\Psi }}^{(\mathrm{U})}$ (Singularity Index)

… ►

$\text{<span class="ltx\_text hilite">umbilics</span>: }{\beta }^{(\mathrm{U})}={\displaystyle \frac{1}{3}}.$

…

9: Bibliography N

… ►

On an integral transform involving a class of Mathieu functions. SIAM J. Math. Anal. 20 (6), pp. 1500–1513.

ⓘ

External Links:

ISSN 0036-1410, Document, MathReview (K. C. Gupta), ZentralBlatt

Referenced by:

§28.26(ii).

Encodings:

BibTeX

… ►

Reduction and evaluation of elliptic integrals. Math. Comp. 20 (94), pp. 223–231.

ⓘ

External Links:

FullText, MathReview (I. A. Stegun), ZentralBlatt

Referenced by:

§19.37(iv).

Encodings:

BibTeX

… ►

A table of integrals of the error functions. J. Res. Nat. Bur. Standards Sect B. 73B, pp. 1–20.

ⓘ

Notes:

See for additions and corrections same journal, Sect. B 75, 149–163 (1975)

External Links:

MathReview, ZentralBlatt

Referenced by:

§7.14(iii), §7.21, §7.7(iii).

Encodings:

BibTeX

… ►

Dislocation lines in the hyperbolic umbilic diffraction catastrophe. Proc. Roy. Soc. Lond. Ser. A 462, pp. 2299–2313.

ⓘ

External Links:

ISSN 1364-5021, Document, MathReview, ZentralBlatt

Referenced by:

§36.7(iv).

Encodings:

BibTeX

►

Dislocation lines in the swallowtail diffraction catastrophe. Proc. Roy. Soc. Lond. Ser. A 463, pp. 343–355.

ⓘ

External Links:

ISSN 1364-5021, Document, ZentralBlatt

Referenced by:

§36.7(iv).

Encodings:

BibTeX

10: 36.11 Leading-Order Asymptotics

§36.11 Leading-Order Asymptotics

… ►

36.11.2 $${\mathrm{\Psi }}_K\left(𝐱\right)=\sqrt{2\pi }\sum _{j=1}^{j_{\max }(𝐱)}\exp \left(\mathrm{i}\left({\mathrm{\Phi }}_K(t_j(𝐱);𝐱)+\frac{1}{4}\pi {(-1)}^{j+K+1}\right)\right){\left|\frac{{\partial }^2{\mathrm{\Phi }}_K(t_j(𝐱);𝐱)}{{\partial t}^2}\right|}^{-1/2}(1+o\left(1\right)).$$

ⓘ

Symbols:

${\mathrm{\Psi }}_K\left(𝐱\right)$: canonical integral function, $\pi$: the ratio of the circumference of a circle to its diameter, ${\mathrm{\Phi }}_K(t;𝐱)$: cuspoid catastrophe of codimension $K$ , $\exp z$: exponential function, $\mathrm{i}$: imaginary unit, $o\left(x\right)$: order less than, $\frac{\partial f}{\partial x}$: partial derivative of $f$ with respect to $x$ , $\partial x$: partial differential of $x$ , $t$: variable, $K$: codimension and $t_j(𝐱)$: solutions

Permalink:

http://dlmf.nist.gov/36.11.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §36.11 and Ch.36

… ►

36.11.7 $${\mathrm{\Psi }}^{(\mathrm{E})}\left(0,0,z\right)=\frac{\pi }{z}\left(\mathrm{i}+\sqrt{3}\exp \left(\frac{4}{27}\mathrm{i}{z}^3\right)+o\left(1\right)\right),$$ $z\to \pm \mathrm{\infty }$,

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, ${\mathrm{\Psi }}^{(\mathrm{E})}\left(𝐱\right)$: elliptic umbilic canonical integral function, $\exp z$: exponential function, $\mathrm{i}$: imaginary unit, $o\left(x\right)$: order less than and $z$: real parameter

Permalink:

http://dlmf.nist.gov/36.11.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §36.11, §36.11 and Ch.36

►

36.11.8 $${\mathrm{\Psi }}^{(\mathrm{H})}\left(0,0,z\right)=\frac{2\pi }{z}\left(1-\frac{\mathrm{i}}{\sqrt{3}}\exp \left(\frac{1}{27}\mathrm{i}{z}^3\right)+o\left(1\right)\right),$$ $z\to \pm \mathrm{\infty }$.

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\exp z$: exponential function, ${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$: hyperbolic umbilic canonical integral function, $\mathrm{i}$: imaginary unit, $o\left(x\right)$: order less than and $z$: real parameter

Permalink:

http://dlmf.nist.gov/36.11.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §36.11, §36.11 and Ch.36