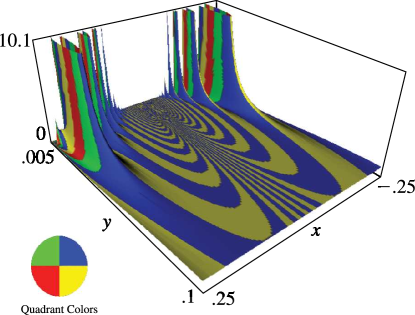
elliptic modular function

SearchAdvancedHelp

(0.005 seconds)

1—10 of 27 matching pages

1: 23.16 Graphics

… ►

►

►

Figure 23.16.2: Elliptic modular function $\lambda \left(x+\mathrm{i}y\right)$ for $-0.25\le x\le 0.25$, $0.005\le y\le 0.1$. Magnify 3D Help

…

2: 23.1 Special Notation

… ►The main functions treated in this chapter are the Weierstrass $\mathrm{\wp }$-function $\mathrm{\wp }\left(z\right)=\mathrm{\wp }\left(z|𝕃\right)=\mathrm{\wp }(z;g_2,g_3)$; the Weierstrass zeta function $\zeta \left(z\right)=\zeta \left(z|𝕃\right)=\zeta (z;g_2,g_3)$; the Weierstrass sigma function $\sigma \left(z\right)=\sigma \left(z|𝕃\right)=\sigma (z;g_2,g_3)$; the elliptic modular function $\lambda \left(\tau \right)$; Klein’s complete invariant $J\left(\tau \right)$; Dedekind’s eta function $\eta \left(\tau \right)$. …

3: 23.19 Interrelations

… ►

23.19.1 $$\lambda \left(\tau \right)=16{\left(\frac{{\eta }^2\left(2\tau \right)\eta \left(\frac{1}{2}\tau \right)}{{\eta }^3\left(\tau \right)}\right)}^8,$$

ⓘ

Symbols:

$\eta \left(\tau \right)$: Dedekind’s eta function (or Dedekind modular function), $\lambda \left(\tau \right)$: elliptic modular function and $\tau$: complex variable

Permalink:

http://dlmf.nist.gov/23.19.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §23.19 and Ch.23

►

23.19.2 $$J\left(\tau \right)=\frac{4}{27}\frac{{\left(1-\lambda \left(\tau \right)+{\lambda }^2\left(\tau \right)\right)}^3}{{\left(\lambda \left(\tau \right)\left(1-\lambda \left(\tau \right)\right)\right)}^2},$$

ⓘ

Symbols:

$J\left(\tau \right)$: Klein’s complete invariant, $\lambda \left(\tau \right)$: elliptic modular function and $\tau$: complex variable

Permalink:

http://dlmf.nist.gov/23.19.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §23.19 and Ch.23

…

4: 23 Weierstrass Elliptic and Modular
Functions

Chapter 23 Weierstrass Elliptic and Modular Functions

…

5: 20.9 Relations to Other Functions

… ►

§20.9(ii) Elliptic Functions and Modular Functions

… ►The relations (20.9.1) and (20.9.2) between $k$ and $\tau$ (or $q$) are solutions of Jacobi’s inversion problem; see Baker (1995) and Whittaker and Watson (1927, pp. 480–485). ►As a function of $\tau$, $k^2$ is the elliptic modular function; see Walker (1996, Chapter 7) and (23.15.2), (23.15.6). …

6: 23.18 Modular Transformations

… ►

Elliptic Modular Function

… ►

23.18.3 $$\lambda \left(𝒜\tau \right)=\lambda \left(\tau \right),$$

ⓘ

Symbols:

$\lambda \left(\tau \right)$: elliptic modular function, $\tau$: complex variable and $𝒜$: bilinear transformation

Permalink:

http://dlmf.nist.gov/23.18.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §23.18, §23.18 and Ch.23

…

7: 23.17 Elementary Properties

… ►

23.17.4 $$\lambda \left(\tau \right)=16q(1-8q+44q^2+\mathrm{\cdots }),$$

ⓘ

Symbols:

$\lambda \left(\tau \right)$: elliptic modular function, $q$: nome and $\tau$: complex variable

Permalink:

http://dlmf.nist.gov/23.17.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §23.17(ii), §23.17 and Ch.23

… ►

23.17.7 $$\lambda \left(\tau \right)=16q\prod _{n=1}^{\mathrm{\infty }}{\left(\frac{1+q^{2n}}{1+q^{2n-1}}\right)}^8,$$

ⓘ

Symbols:

$\lambda \left(\tau \right)$: elliptic modular function, $q$: nome, $n$: integer and $\tau$: complex variable

Permalink:

http://dlmf.nist.gov/23.17.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §23.17(iii), §23.17 and Ch.23

…

8: Peter L. Walker

… ►

23 Weierstrass Elliptic and Modular Functions

…

9: 23.15 Definitions

… ►

Elliptic Modular Function

►

23.15.6 $$\lambda \left(\tau \right)=\frac{{\theta }_2^4(0,q)}{{\theta }_3^4(0,q)};$$

ⓘ

Defines:

$\lambda \left(\tau \right)$: elliptic modular function

Symbols:

${\theta }_j(z,q)$: theta function, $q$: nome and $\tau$: complex variable

Referenced by:

§20.9(ii), §23.17(iii)

Permalink:

http://dlmf.nist.gov/23.15.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §23.15(ii), §23.15(ii), §23.15 and Ch.23

…

10: Ranjan Roy

… ►He also authored another two advanced mathematics books: Sources in the development of mathematics (Roy, 2011), Elliptic and modular functions from Gauss to Dedekind to Hecke (Roy, 2017). …