defined by contour integrals

SearchAdvancedHelp

(0.002 seconds)

1—10 of 15 matching pages

1: 9.14 Incomplete Airy Functions

… ►Incomplete Airy functions are defined by the contour integral (9.5.4) when one of the integration limits is replaced by a variable real or complex parameter. …

2: 1.10 Functions of a Complex Variable

… ►

§1.10(viii) Functions Defined by Contour Integrals

…

3: 2.10 Sums and Sequences

… ►The asymptotic behavior of entire functions defined by Maclaurin series can be approached by converting the sum into a contour integral by use of the residue theorem and applying the methods of §§2.4 and 2.5. …

4: 21.7 Riemann Surfaces

… ►Then the matrix defined by …is a Riemann matrix and it is used to define the corresponding Riemann theta function. … ►Define the holomorphic differential …Then the prime form on the corresponding compact Riemann surface $\mathrm{\Gamma }$ is defined by … ►Define the operation …

5: 1.9 Calculus of a Complex Variable

… ►

§1.9(iii) Integration

… ►If $x(t)$ and $y(t)$ are continuous and $x^{\prime }(t)$ and $y^{\prime }(t)$ are piecewise continuous, then $z(t)$ defines a contour. … ►A simple closed contour is a simple contour, except that $z(a)=z(b)$. … ►

Winding Number

…

6: Errata

… ►

The material surrounding (19.2.8), (19.2.9) has been updated so that the complementary complete elliptic integrals of the first and second kind are defined with consistent multivalued properties and correct analytic continuation. In particular, (19.2.9) has been corrected to read

19.2.9

… ►

10.23.11 $$a_k=\frac{1}{2\pi i}{\int }_{|t|=c^{\prime }}f(t)O_k\left(t\right)dt,$$

Originally the contour of integration written incorrectly as $|z|=c^{\prime }$, has been corrected to be $|t|=c^{\prime }$.

Reported by Mark Dunster on 2021-03-22

… ►

There have been extensive changes in the notation used for the integral transforms defined in §1.14. These changes are applied throughout the DLMF. The following table summarizes the changes.

Transform	New	Abbreviated	Old
	Notation	Notation	Notation
Fourier	$ℱ\left(f\right)\left(x\right)$	$ℱf\left(x\right)$
Fourier Cosine	${ℱ}_c\left(f\right)\left(x\right)$	${ℱ}_{c}f\left(x\right)$
Fourier Sine	${ℱ}_s\left(f\right)\left(x\right)$	${ℱ}_{s}f\left(x\right)$
Laplace	$ℒ\left(f\right)\left(s\right)$	$ℒf\left(s\right)$	$ℒ(f(t);s)$
Mellin	$ℳ\left(f\right)\left(s\right)$	$ℳf\left(s\right)$	$ℳ(f;s)$
Hilbert	$\mathscr{H}\left(f\right)\left(s\right)$	$\mathscr{H}f\left(s\right)$	$\mathscr{H}(f;s)$
Stieltjes	$𝒮\left(f\right)\left(s\right)$	$𝒮f\left(s\right)$	$𝒮(f;s)$

Previously, for the Fourier, Fourier cosine and Fourier sine transforms, either temporary local notations were used or the Fourier integrals were written out explicitly.

… ►

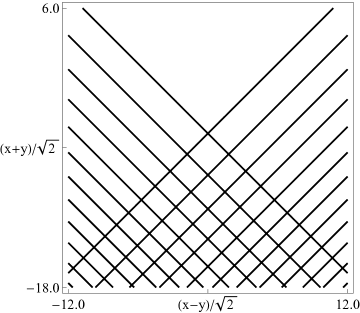
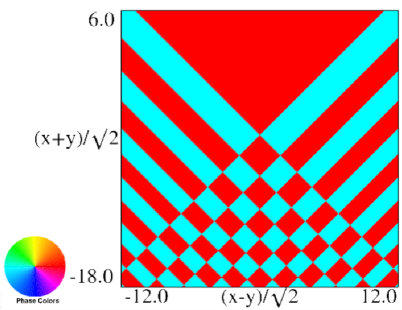
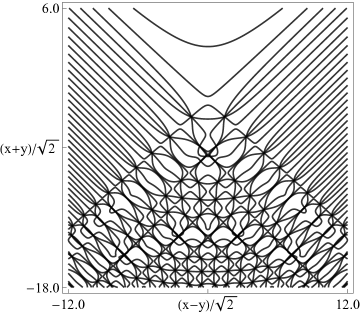
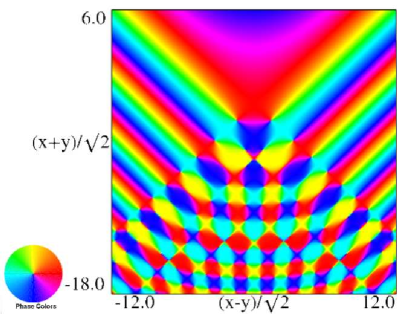
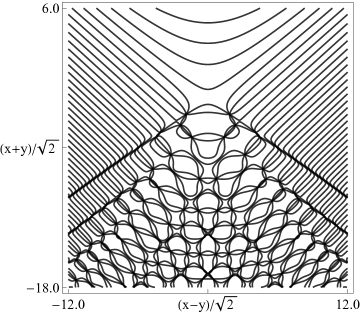
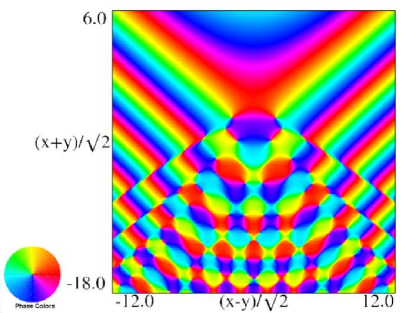
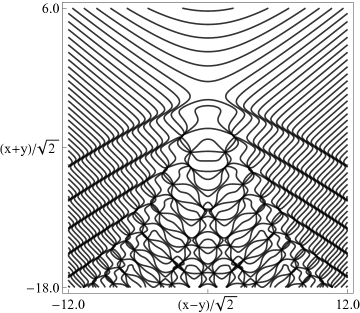
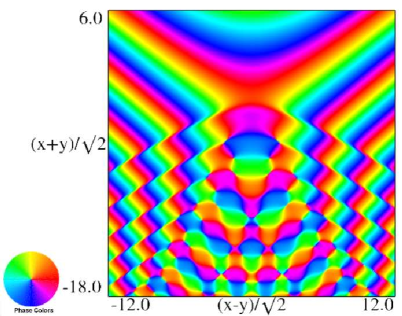
The scaling error reported on 2016-09-12 by Dan Piponi also applied to contour and density plots for the phase of the hyperbolic umbilic canonical integrals. Scales were corrected in all figures. The interval $-8.4\le \frac{x-y}{\sqrt{2}}\le 8.4$ was replaced by $-12.0\le \frac{x-y}{\sqrt{2}}\le 12.0$ and $-12.7\le \frac{x+y}{\sqrt{2}}\le 4.2$ replaced by $-18.0\le \frac{x+y}{\sqrt{2}}\le 6.0$. All plots and interactive visualizations were regenerated to improve image quality.

(a) Contour plot.	(b) Density plot.

Figure 36.3.18: Phase of hyperbolic umbilic canonical integral $\mathrm{ph}{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,0\right)$.

(a) Contour plot.	(b) Density plot.

Figure 36.3.19: Phase of hyperbolic umbilic canonical integral $\mathrm{ph}{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,1\right)$.

(a) Contour plot.	(b) Density plot.

Figure 36.3.20: Phase of hyperbolic umbilic canonical integral $\mathrm{ph}{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,2\right)$.

(a) Contour plot.	(b) Density plot.

Figure 36.3.21: Phase of hyperbolic umbilic canonical integral $\mathrm{ph}{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,3\right)$.

Reported 2016-09-28.

… ►

A number of changes were made with regard to fractional integrals and derivatives. In §1.15(vi) a reference to Miller and Ross (1993) was added, the fractional integral operator of order $\alpha$ was more precisely identified as the Riemann-Liouville fractional integral operator of order $\alpha$, and a paragraph was added below (1.15.50) to generalize (1.15.47). In §1.15(vii) the sentence defining the fractional derivative was clarified. In §2.6(iii) the identification of the Riemann-Liouville fractional integral operator was made consistent with §1.15(vi).

…

7: 9.13 Generalized Airy Functions

… ►For properties of the zeros of the functions defined in this subsection see Laforgia and Muldoon (1988) and references given therein. … ►

§9.13(ii) Generalizations from Integral Representations

►Reid (1972) and Drazin and Reid (1981, Appendix) introduce the following contour integrals in constructing approximate solutions to the Orr–Sommerfeld equation for fluid flow: … ►Further properties of these functions, and also of similar contour integrals containing an additional factor ${(\ln t)}^q$, $q=1,2,\mathrm{\dots }$, in the integrand, are derived in Reid (1972), Drazin and Reid (1981, Appendix), and Baldwin (1985). … ►

8: 10.23 Sums

… ►Define … ►

10.23.11 $$a_k=\frac{1}{2\pi \mathrm{i}}{\int }_{|t|=c^{\prime }}f(t)O_k\left(t\right)dt,$$ ,

ⓘ

Defines:

$a_k$ (locally)

Symbols:

$O_n\left(x\right)$: Neumann’s polynomial, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{i}$: imaginary unit, $\int$: integral, $k$: nonnegative integer, $z$: complex variable and $f(t)$

A&S Ref:

9.1.83

Referenced by:

Erratum (V1.1.2) for Equation (10.23.11)

Permalink:

http://dlmf.nist.gov/10.23.E11

Encodings:

pMML, png, TeX

Errata (effective with 1.1.2):

Originally the contour of integration written incorrectly as $|z|=c^{\prime }$, has been corrected to be $|t|=c^{\prime }$.

Reported 2021-03-22 by Mark Dunster

See also:

Annotations for §10.23(iii), §10.23(iii), §10.23 and Ch.10

►and $O_k\left(t\right)$ is Neumann’s polynomial, defined by the generating function: … ►

10.23.18

ⓘ

Symbols:

$dx$: differential of $x$ , $\int$: integral and $f(t)$

Permalink:

http://dlmf.nist.gov/10.23.E18

Encodings:

pMML, png, TeX

See also:

Annotations for §10.23(iii), §10.23(iii), §10.23 and Ch.10

►and define …

9: 9.17 Methods of Computation

… ►A comprehensive and powerful approach is to integrate the defining differential equation (9.2.1) by direct numerical methods. … ►

§9.17(iii) Integral Representations

►Among the integral representations of the Airy functions the Stieltjes transform (9.10.18) furnishes a way of computing $\mathrm{Ai}\left(z\right)$ in the complex plane, once values of this function can be generated on the positive real axis. … ►In the first method the integration path for the contour integral (9.5.4) is deformed to coincide with paths of steepest descent (§2.4(iv)). …The second method is to apply generalized Gauss–Laguerre quadrature (§3.5(v)) to the integral (9.5.8). …

10: 15.9 Relations to Other Functions

… ►The Jacobi transform is defined as ►

15.9.12 $$\tilde{f}(\lambda )={\int }_0^{\mathrm{\infty }}f(t){\varphi }_{\lambda }^{(\alpha ,\beta )}\left(t\right){(2\sinh t)}^{2\alpha +1}{(2\cosh t)}^{2\beta +1}dt,$$

ⓘ

Symbols:

${\varphi }_{\lambda }^{(\alpha ,\beta )}\left(t\right)$: Jacobi function, $dx$: differential of $x$ , $\cosh z$: hyperbolic cosine function, $\sinh z$: hyperbolic sine function, $\int$: integral and $f(t)$: function

Permalink:

http://dlmf.nist.gov/15.9.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §15.9(ii), §15.9 and Ch.15

… ►where the contour of integration is located to the right of the poles of the gamma functions in the integrand, and … ►It is defined by: … ►

§15.9(v) Complete Elliptic Integrals

…