conjugate

SearchAdvancedHelp

(0.000 seconds)

1—10 of 78 matching pages

1: 1.1 Special Notation

… ► ►►►►

$x,y$	real variables.
…
$\overline{𝐀}$	complex conjugate of the matrix $𝐀$
…
${𝐀}^{\mathrm{H}}$	Hermitian conjugate of the matrix $𝐀$
…

►In the physics, applied maths, and engineering literature a common alternative to $\overline{a}$ is $a^{\ast }$, $a$ being a complex number or a matrix; the Hermitian conjugate of $𝐀$ is usually being denoted ${𝐀}^{†}$.

2: 18.19 Hahn Class: Definitions

… ► ►

18.19.1 $$p_n(x)=p_n(x;a,b,\overline{a},\overline{b}),$$

ⓘ

Symbols:

$\overline{z}$: complex conjugate, $p_n(x;a,b,\overline{a},\overline{b})$: continuous Hahn polynomial, $p_n(x)$: polynomial of degree $n$ , $n$: nonnegative integer and $x$: real variable

Referenced by:

§18.19

Permalink:

http://dlmf.nist.gov/18.19.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §18.19, §18.19 and Ch.18

►

18.19.2 $$w(z;a,b,\overline{a},\overline{b})=\mathrm{\Gamma }\left(a+iz\right)\mathrm{\Gamma }\left(b+iz\right)\mathrm{\Gamma }\left(\overline{a}-iz\right)\mathrm{\Gamma }\left(\overline{b}-iz\right),$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\overline{z}$: complex conjugate, $w(x)$: weight function and $z$: complex variable

Permalink:

http://dlmf.nist.gov/18.19.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §18.19, §18.19 and Ch.18

►

18.19.3 $$w(x)=w(x;a,b,\overline{a},\overline{b})={|\mathrm{\Gamma }\left(a+\mathrm{i}x\right)\mathrm{\Gamma }\left(b+\mathrm{i}x\right)|}^2,$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\overline{z}$: complex conjugate, $\mathrm{i}$: imaginary unit, $w(x)$: weight function and $x$: real variable

Permalink:

http://dlmf.nist.gov/18.19.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §18.19, §18.19 and Ch.18

►

18.19.4 $$h_n=\frac{2\pi \mathrm{\Gamma }\left(n+a+\overline{a}\right)\mathrm{\Gamma }\left(n+b+\overline{b}\right){|\mathrm{\Gamma }\left(n+a+\overline{b}\right)|}^2}{\left(2n+2\mathrm{\Re }\left(a+b\right)-1\right)\mathrm{\Gamma }\left(n+2\mathrm{\Re }\left(a+b\right)-1\right)n!},$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\overline{z}$: complex conjugate, $!$: factorial (as in $n!$), $\mathrm{\Re }$: real part, $n$: nonnegative integer and $h_n$

Referenced by:

§18.19

Permalink:

http://dlmf.nist.gov/18.19.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §18.19, §18.19 and Ch.18

…

3: 18.33 Polynomials Orthogonal on the Unit Circle

… ►where the bar signifies complex conjugate. … ►where the bar again signifies complex conjugate. … ►where the bar signifies complex conjugate and ${\kappa }_n>0$, ${\kappa }_0=1$. … ►

18.33.22 $$p^{\ast }(z)\equiv z^n\overline{p({\overline{z}}^{-1})}=\sum _{k=0}^n\overline{c_{n-k}}{z}^k.$$

ⓘ

Symbols:

$\overline{z}$: complex conjugate, $\equiv$: equals by definition, $z$: complex variable, $k$: nonnegative integer and $n$: nonnegative integer

Source:

Simon (2005a, (1.1.7))

Permalink:

http://dlmf.nist.gov/18.33.E22

Encodings:

pMML, png, TeX

See also:

Annotations for §18.33(vi), §18.33(vi), §18.33 and Ch.18

… ►for $n>0$, while ${\mathrm{\Phi }}_1(z)=z-\overline{{\alpha }_0}$. …

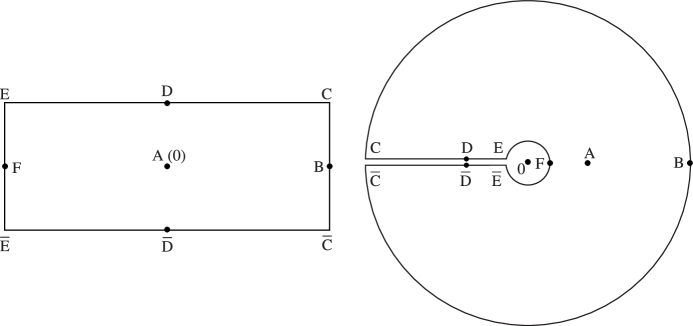
4: 4.3 Graphics

… ►Corresponding points share the same letters, with bars signifying complex conjugates. … ►

►

… ►

►►

	A	B	C	$\overline{\mathrm{C}}$	D	$\overline{\mathrm{D}}$	E	$\overline{\mathrm{E}}$	F
…

►

Figure 4.3.2: Conformal mapping of exponential and logarithm. … Magnify

…

5: 18.20 Hahn Class: Explicit Representations

… ►

18.20.3 $$w(x;a,b,\overline{a},\overline{b})p_n(x;a,b,\overline{a},\overline{b})=\frac{1}{n!}{\delta }_x^n\left(w(x;a+\frac{1}{2}n,b+\frac{1}{2}n,\overline{a}+\frac{1}{2}n,\overline{b}+\frac{1}{2}n)\right).$$

ⓘ

Symbols:

${\delta }_x$: central difference, $\overline{z}$: complex conjugate, $p_n(x;a,b,\overline{a},\overline{b})$: continuous Hahn polynomial, $!$: factorial (as in $n!$), $n$: nonnegative integer and $x$: real variable

Referenced by:

§18.20(i)

Permalink:

http://dlmf.nist.gov/18.20.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §18.20(i), §18.20(i), §18.20 and Ch.18

… ►

18.20.9 $$p_n(x;a,b,\overline{a},\overline{b})=\frac{{\mathrm{i}}^n{\left(a+\overline{a}\right)}_n{\left(a+\overline{b}\right)}_n}{n!}{}_3{}^{}F_2^{}(\genfrac{}{}{0pt}{}{-n,n+2\mathrm{\Re }\left(a+b\right)-1,a+\mathrm{i}x}{a+\overline{a},a+\overline{b}};1).$$

ⓘ

Symbols:

${}_p{}^{}F_q^{}(a_1,\mathrm{\dots },a_p;b_1,\mathrm{\dots },b_q;z)$ or ${}_p{}^{}F_q^{}(\genfrac{}{}{0pt}{}{a_1,\mathrm{\dots },a_p}{b_1,\mathrm{\dots },b_q};z)$: alternatively ${}_p{}^{}F_q^{}(𝐚;𝐛;z)$ or ${}_p{}^{}F_q^{}(\genfrac{}{}{0pt}{}{𝐚}{𝐛};z)$
generalized hypergeometric function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\overline{z}$: complex conjugate, $p_n(x;a,b,\overline{a},\overline{b})$: continuous Hahn polynomial, $!$: factorial (as in $n!$), $\mathrm{i}$: imaginary unit, $\mathrm{\Re }$: real part, $n$: nonnegative integer and $x$: real variable

Referenced by:

§18.19, §18.20(ii), §18.21(ii), §18.22(iii), §18.26(ii)

Permalink:

http://dlmf.nist.gov/18.20.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §18.20(ii), §18.20 and Ch.18

►(For symmetry properties of $p_n(x;a,b,\overline{a},\overline{b})$ with respect to $a$, $b$, $\overline{a}$, $\overline{b}$ see Andrews et al. (1999, Corollary 3.3.4).) …

6: 18.22 Hahn Class: Recurrence Relations and Differences

… ►

18.22.4 $$q_n(x)=p_n(x;a,b,\overline{a},\overline{b})/p_n(\mathrm{i}a;a,b,\overline{a},\overline{b}),$$

ⓘ

Symbols:

$\overline{z}$: complex conjugate, $p_n(x;a,b,\overline{a},\overline{b})$: continuous Hahn polynomial, $\mathrm{i}$: imaginary unit, $n$: nonnegative integer and $x$: real variable

Referenced by:

§18.22(i)

Permalink:

http://dlmf.nist.gov/18.22.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §18.22(i), §18.22(i), §18.22 and Ch.18

… ►

18.22.13 $$p_n(x)=p_n(x;a,b,\overline{a},\overline{b}),$$

ⓘ

Symbols:

$\overline{z}$: complex conjugate, $p_n(x;a,b,\overline{a},\overline{b})$: continuous Hahn polynomial, $p_n(x)$: polynomial of degree $n$ , $n$: nonnegative integer and $x$: real variable

Referenced by:

§18.22(ii)

Permalink:

http://dlmf.nist.gov/18.22.E13

Encodings:

pMML, png, TeX

See also:

Annotations for §18.22(ii), §18.22(ii), §18.22 and Ch.18

… ►

$A(x)=(x+\mathrm{i}\overline{a})(x+\mathrm{i}\overline{b}),$

… ►

18.22.27 $${\delta }_x\left(p_n(x;a,b,\overline{a},\overline{b})\right)=(n+2\mathrm{\Re }\left(a+b\right)-1)p_{n-1}(x;a+\frac{1}{2},b+\frac{1}{2},\overline{a}+\frac{1}{2},\overline{b}+\frac{1}{2}),$$

ⓘ

Symbols:

${\delta }_x$: central difference, $\overline{z}$: complex conjugate, $p_n(x;a,b,\overline{a},\overline{b})$: continuous Hahn polynomial, $\mathrm{\Re }$: real part, $n$: nonnegative integer and $x$: real variable

Referenced by:

§18.22(iii)

Permalink:

http://dlmf.nist.gov/18.22.E27

Encodings:

pMML, png, TeX

See also:

Annotations for §18.22(iii), §18.22(iii), §18.22 and Ch.18

►

18.22.28 $${\delta }_x\left(w(x;a+\frac{1}{2},b+\frac{1}{2},\overline{a}+\frac{1}{2},\overline{b}+\frac{1}{2})p_n(x;a+\frac{1}{2},b+\frac{1}{2},\overline{a}+\frac{1}{2},\overline{b}+\frac{1}{2})\right)=-(n+1)w(x;a,b,\overline{a},\overline{b})p_{n+1}(x;a,b,\overline{a},\overline{b}).$$

ⓘ

Symbols:

${\delta }_x$: central difference, $\overline{z}$: complex conjugate, $p_n(x)$: polynomial of degree $n$ , $w(x)$: weight function, $n$: nonnegative integer and $x$: real variable

Referenced by:

§18.20(i), §18.22(iii)

Permalink:

http://dlmf.nist.gov/18.22.E28

Encodings:

pMML, png, TeX

See also:

Annotations for §18.22(iii), §18.22(iii), §18.22 and Ch.18

…

7: 12.21 Software

…

8: 36.8 Convergent Series Expansions

… ►

36.8.5 $$f_n(\zeta ,\overline{\zeta })=c_n(\zeta )c_n(\overline{\zeta })\mathrm{Ai}\left(\zeta \right)\mathrm{Bi}\left(\overline{\zeta }\right)+c_n(\zeta )d_n(\overline{\zeta })\mathrm{Ai}\left(\zeta \right){\mathrm{Bi}}^{\prime }\left(\overline{\zeta }\right)+d_n(\zeta )c_n(\overline{\zeta }){\mathrm{Ai}}^{\prime }\left(\zeta \right)\mathrm{Bi}\left(\overline{\zeta }\right)+d_n(\zeta )d_n(\overline{\zeta }){\mathrm{Ai}}^{\prime }\left(\zeta \right){\mathrm{Bi}}^{\prime }\left(\overline{\zeta }\right),$$

ⓘ

Defines:

$f_n$: function (locally)

Symbols:

$\mathrm{Ai}\left(z\right)$: Airy function, $\mathrm{Bi}\left(z\right)$: Airy function, $\overline{z}$: complex conjugate, $m$: integer, $c_n(t)$: coefficients and $d_n(t)$: coefficients

Permalink:

http://dlmf.nist.gov/36.8.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §36.8 and Ch.36

…

9: 10.34 Analytic Continuation

… ►

$I_{\nu }\left(\overline{z}\right)=\overline{I_{\nu }\left(z\right)},$

►

$K_{\nu }\left(\overline{z}\right)=\overline{K_{\nu }\left(z\right)}.$

►For complex $\nu$ replace $\nu$ by $\overline{\nu }$ on the right-hand sides.

10: 12.3 Graphics

… ►

►►

Figure 12.3.5: $U(-8,x)$, $\overline{U}(-8,x)$, $F(-8,x)$, $-4\sqrt{2}\le x\le 4\sqrt{2}$. Magnify

►

►►

Figure 12.3.6: $U^{\prime }(-8,x)$, ${\overline{U}}^{\prime }(-8,x)$, $G(-8,x)$, $-4\sqrt{2}\le x\le 4\sqrt{2}$. Magnify

…