classical orthogonal polynomials

SearchAdvancedHelp

(0.012 seconds)

1—10 of 44 matching pages

1: 18.3 Definitions

§18.3 Definitions

… ►

With the property that ${\{p_{n+1}^{\prime }(x)\}}_{n=0}^{\mathrm{\infty }}$ is again a system of OP’s. See §18.9(iii).

►

As given by a Rodrigues formula (18.5.5).

… ►

Table 18.3.1: Orthogonality properties for classical OP’s: intervals, weight functions, standardizations, leading coefficients, and parameter constraints. …

► ►►

Name	$p_n(x)$	$(a,b)$	$w(x)$	$h_n$	$k_n$	${\tilde{k}}_n/k_n$	Constraints
…

►

… ►For explicit power series coefficients up to $n=12$ for these polynomials and for coefficients up to $n=6$ for Jacobi and ultraspherical polynomials see Abramowitz and Stegun (1964, pp. 793–801). …

2: 18.41 Tables

… ►For $P_n\left(x\right)$ ($={𝖯}_n\left(x\right)$) see §14.33. …

3: 18.38 Mathematical Applications

… ►

§18.38(i) Classical OP’s: Numerical Analysis

… ►

Quadrature

… ►

Integrable Systems

… ►

Riemann–Hilbert Problems

… ►

Radon Transform

…

4: 18.13 Continued Fractions

§18.13 Continued Fractions

… ►See also Cuyt et al. (2008, pp. 91–99).

5: 18.7 Interrelations and Limit Relations

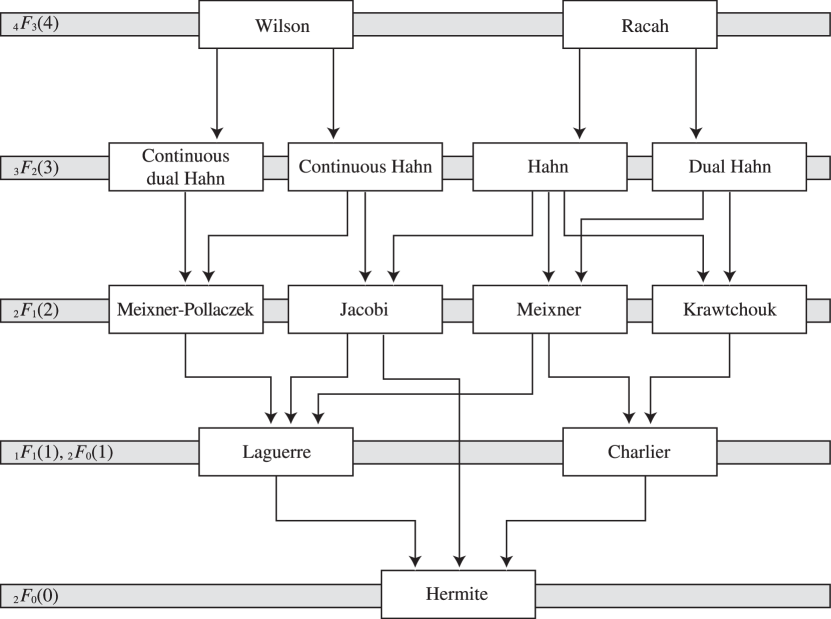
§18.7 Interrelations and Limit Relations

►

§18.7(i) Linear Transformations

… ►

§18.7(ii) Quadratic Transformations

… ►Equations (18.7.13)–(18.7.20) are special cases of (18.2.22)–(18.2.23). ►

§18.7(iii) Limit Relations

…

6: 18.5 Explicit Representations

§18.5 Explicit Representations

… ►

Table 18.5.1: Classical OP’s: Rodrigues formulas (18.5.5).

► ►►

$p_n(x)$	$w(x)$	$F(x)$	${\kappa }_n$
…

►

… ►

§18.5(iii) Finite Power Series, the Hypergeometric Function, and Generalized Hypergeometric Functions

… ► … ►

7: 18.16 Zeros

… ►

Inequalities

… ►

Asymptotic Behavior

… ►when $\alpha \notin (-\frac{1}{2},\frac{1}{2})$. … ►For further information on the zeros of the classical orthogonal polynomials, see Szegő (1975, Chapter VI), Erdélyi et al. (1953b, §§10.16 and 10.17), Gatteschi (1987, 2002), López and Temme (1999a), and Temme (1990a). ►

§18.16(vii) Discriminants

…

8: 18.14 Inequalities

… ►

§18.14(i) Upper Bounds

… ►

§18.14(ii) Turán-Type Inequalities

… ►

§18.14(iii) Local Maxima and Minima

… ►The successive maxima of $|H_n\left(x\right)|$ form a decreasing sequence for $x\le 0$, and an increasing sequence for $x\ge 0$. ►

§18.14(iv) Positive Sums

…

9: 18.18 Sums

§18.18 Sums

… ►

§18.18(ii) Addition Theorems

… ►

§18.18(iii) Multiplication Theorems

… ►

§18.18(v) Linearization Formulas

… ►

10: 18.21 Hahn Class: Interrelations

… ►

►►

Figure 18.21.1: Askey scheme. … Magnify