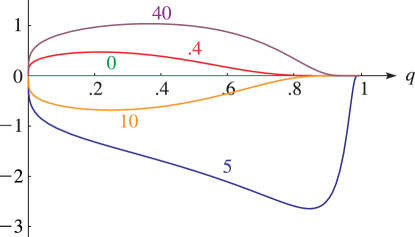
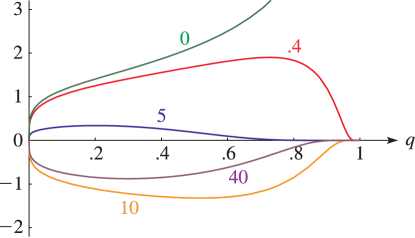
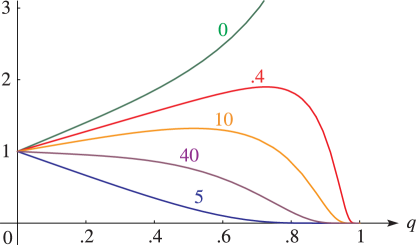
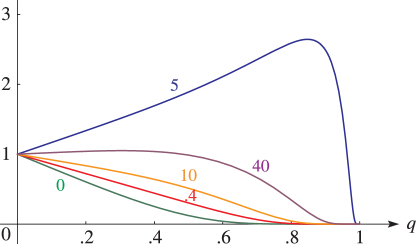
as x→±1

SearchAdvancedHelp

(0.042 seconds)

1—10 of 629 matching pages

1: 18.8 Differential Equations

… ►

Table 18.8.1: Classical OP’s: differential equations $A(x)f^{\prime \prime }(x)+B(x)f^{\prime }(x)+C(x)f(x)+{\lambda }_{n}f(x)=0$.

► ►►►►►►►

#	$f(x)$	$A(x)$	$B(x)$	$C(x)$	${\lambda }_n$
…
4	$C_n^{(\lambda )}\left(x\right)$	$1-x^2$	$-(2\lambda +1)x$	$0$	$n(n+2\lambda )$
5	$T_n\left(x\right)$	$1-x^2$	$-x$	$0$	$n^2$
…
7	$P_n\left(x\right)$	$1-x^2$	$-2x$	$0$	$n(n+1)$
…
12	$H_n\left(x\right)$	$1$	$-2x$	$0$	$2n$
…
14	${\mathrm{𝐻𝑒}}_n\left(x\right)$	$1$	$-x$	$0$	$n$

►

…

2: 18.31 Bernstein–Szegő Polynomials

… ►Let $\rho (x)$ be a polynomial of degree $\mathrm{\ell }$ and positive when $-1\le x\le 1$. The Bernstein–Szegő polynomials $\{p_n(x)\}$, $n=0,1,\mathrm{\dots }$, are orthogonal on $(-1,1)$ with respect to three types of weight function: ${(1-x^2)}^{-\frac{1}{2}}{(\rho (x))}^{-1}$, ${(1-x^2)}^{\frac{1}{2}}{(\rho (x))}^{-1}$, ${(1-x)}^{\frac{1}{2}}{(1+x)}^{-\frac{1}{2}}{(\rho (x))}^{-1}$. …

3: 4.5 Inequalities

… ►

4.5.1 $x>-1$, $x\ne 0$,

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function and $x$: real variable

A&S Ref:

4.1.33

Referenced by:

§4.5(i), §4.5(ii)

Permalink:

http://dlmf.nist.gov/4.5.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §4.5(i), §4.5 and Ch.4

►

4.5.2 , $x\ne 0$,

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function and $x$: real variable

A&S Ref:

4.1.34

Referenced by:

§4.5(i), §4.5(ii)

Permalink:

http://dlmf.nist.gov/4.5.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §4.5(i), §4.5 and Ch.4

… ►

4.5.7 ,

ⓘ

Symbols:

$\mathrm{e}$: base of natural logarithm and $x$: real variable

A&S Ref:

4.2.29

Referenced by:

§4.5(ii), §4.5(ii)

Permalink:

http://dlmf.nist.gov/4.5.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §4.5(ii), §4.5 and Ch.4

… ►

4.5.11 ,

ⓘ

Symbols:

$\mathrm{e}$: base of natural logarithm and $x$: real variable

A&S Ref:

4.2.33

Permalink:

http://dlmf.nist.gov/4.5.E11

Encodings:

pMML, png, TeX

See also:

Annotations for §4.5(ii), §4.5 and Ch.4

►

4.5.12 $x>-1$,

ⓘ

Symbols:

$\mathrm{e}$: base of natural logarithm and $x$: real variable

A&S Ref:

4.2.34

Referenced by:

§4.5(ii), §4.5(ii)

Permalink:

http://dlmf.nist.gov/4.5.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §4.5(ii), §4.5 and Ch.4

…

4: 6.8 Inequalities

… ►

6.8.1

ⓘ

Symbols:

$\mathrm{e}$: base of natural logarithm, $E_1\left(z\right)$: exponential integral, $\ln z$: principal branch of logarithm function and $x$: real variable

A&S Ref:

5.1.20

Referenced by:

§6.8

Permalink:

http://dlmf.nist.gov/6.8.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §6.8 and Ch.6

►

6.8.2

ⓘ

Symbols:

$\mathrm{e}$: base of natural logarithm, $E_1\left(z\right)$: exponential integral and $x$: real variable

Referenced by:

§6.8

Permalink:

http://dlmf.nist.gov/6.8.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §6.8 and Ch.6

►

6.8.3

ⓘ

Symbols:

$\mathrm{e}$: base of natural logarithm, $E_1\left(z\right)$: exponential integral and $x$: real variable

Referenced by:

§6.8

Permalink:

http://dlmf.nist.gov/6.8.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §6.8 and Ch.6

5: 14.10 Recurrence Relations and Derivatives

… ►

14.10.1 $${𝖯}_{\nu }^{\mu +2}\left(x\right)+2(\mu +1)x{\left(1-x^2\right)}^{-1/2}{𝖯}_{\nu }^{\mu +1}\left(x\right)+(\nu -\mu )(\nu +\mu +1){𝖯}_{\nu }^{\mu }\left(x\right)=0,$$

ⓘ

Symbols:

: Ferrers function of the first kind, $x$: real variable, $\mu$: general order and $\nu$: general degree

Referenced by:

§14.10

Permalink:

http://dlmf.nist.gov/14.10.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §14.10 and Ch.14

►

14.10.2 $${\left(1-x^2\right)}^{1/2}{𝖯}_{\nu }^{\mu +1}\left(x\right)-(\nu -\mu +1){𝖯}_{\nu +1}^{\mu }\left(x\right)+(\nu +\mu +1)x{𝖯}_{\nu }^{\mu }\left(x\right)=0,$$

ⓘ

Symbols:

: Ferrers function of the first kind, $x$: real variable, $\mu$: general order and $\nu$: general degree

Permalink:

http://dlmf.nist.gov/14.10.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §14.10 and Ch.14

… ►

14.10.4 $$\left(1-x^2\right)\frac{d{𝖯}_{\nu }^{\mu }\left(x\right)}{dx}=(\mu -\nu -1){𝖯}_{\nu +1}^{\mu }\left(x\right)+(\nu +1)x{𝖯}_{\nu }^{\mu }\left(x\right),$$

ⓘ

Symbols:

: Ferrers function of the first kind, $\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $x$: real variable, $\mu$: general order and $\nu$: general degree

Referenced by:

§14.5(i)

Permalink:

http://dlmf.nist.gov/14.10.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §14.10 and Ch.14

… ►

14.10.6 $$P_{\nu }^{\mu +2}\left(x\right)+2(\mu +1)x{\left(x^2-1\right)}^{-1/2}{P}_{\nu }^{\mu +1}\left(x\right)-(\nu -\mu )(\nu +\mu +1)P_{\nu }^{\mu }\left(x\right)=0,$$

ⓘ

Symbols:

$P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, $x$: real variable, $\mu$: general order and $\nu$: general degree

Referenced by:

§14.10, §14.14

Permalink:

http://dlmf.nist.gov/14.10.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §14.10 and Ch.14

►

14.10.7 $${\left(x^2-1\right)}^{1/2}{P}_{\nu }^{\mu +1}\left(x\right)-(\nu -\mu +1)P_{\nu +1}^{\mu }\left(x\right)+(\nu +\mu +1)x{P}_{\nu }^{\mu }\left(x\right)=0.$$

ⓘ

Symbols:

$P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, $x$: real variable, $\mu$: general order and $\nu$: general degree

Referenced by:

§14.10, §14.21(iii)

Permalink:

http://dlmf.nist.gov/14.10.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §14.10 and Ch.14

…

6: 12.6 Continued Fraction

… ►For a continued-fraction expansion of the ratio $U(a,x)/U(a-1,x)$ see Cuyt et al. (2008, pp. 340–341).

7: 4.12 Generalized Logarithms and Exponentials

… ►

4.12.1 $$\varphi (x+1)={\mathrm{e}}^{\varphi (x)},$$ ,

ⓘ

Symbols:

$\mathrm{e}$: base of natural logarithm, $x$: real variable and $\varphi (z)$: generalized exponential

Permalink:

http://dlmf.nist.gov/4.12.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §4.12 and Ch.4

… ►and is strictly increasing when $0\le x\le 1$. …It, too, is strictly increasing when $0\le x\le 1$, and … ►

4.12.5 $$\varphi (x)=\psi (x)=x,$$ $0\le x\le 1$.

ⓘ

Symbols:

$x$: real variable, $\varphi (z)$: generalized exponential and $\psi (x)$: generalized logarithm

Permalink:

http://dlmf.nist.gov/4.12.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §4.12 and Ch.4

… ►

4.12.6 $$\varphi (x)=\ln \left(x+1\right),$$ ,

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function, $x$: real variable and $\varphi (z)$: generalized exponential

Permalink:

http://dlmf.nist.gov/4.12.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §4.12 and Ch.4

…

8: 27.7 Lambert Series as Generating Functions

… ►

27.7.1 $$\sum _{n=1}^{\mathrm{\infty }}f(n)\frac{x^n}{1-x^n}.$$

ⓘ

Symbols:

$n$: positive integer and $x$: real number

Referenced by:

§27.7

Permalink:

http://dlmf.nist.gov/27.7.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §27.7 and Ch.27

►If , then the quotient $x^n/(1-x^n)$ is the sum of a geometric series, and when the series (27.7.1) converges absolutely it can be rearranged as a power series: … ►Again with , special cases of (27.7.2) include: ►

27.7.3 $$\sum _{n=1}^{\mathrm{\infty }}\mu \left(n\right)\frac{x^n}{1-x^n}=x,$$

ⓘ

Symbols:

$\mu \left(n\right)$: Möbius function, $n$: positive integer and $x$: real number

A&S Ref:

24.3.1 I.B

Permalink:

http://dlmf.nist.gov/27.7.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §27.7 and Ch.27

►

27.7.4 $$\sum _{n=1}^{\mathrm{\infty }}\varphi \left(n\right)\frac{x^n}{1-x^n}=\frac{x}{{(1-x)}^2},$$

ⓘ

Symbols:

$\varphi \left(n\right)$: Euler’s totient, $n$: positive integer and $x$: real number

A&S Ref:

24.3.2 I.B

Permalink:

http://dlmf.nist.gov/27.7.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §27.7 and Ch.27

…

9: 19.32 Conformal Map onto a Rectangle

… ►with $x_1,x_2,x_3$ real constants, has differential … ►

19.32.3 $$x_1>x_2>x_3,$$

ⓘ

Permalink:

http://dlmf.nist.gov/19.32.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §19.32 and Ch.19

… ►

$$z(x_1)=R_F(0,x_1-x_2,x_1-x_3)\text{(}>0\text{)},$$

►

$$z(x_2)=z(x_1)+z(x_3),$$

►

$$z(x_3)=R_F(x_3-x_1,x_3-x_2,0)=-\mathrm{i}{R}_F(0,x_1-x_3,x_2-x_3).$$

…

10: 20.3 Graphics

… ►

►►

Figure 20.3.6: ${\theta }_1(x,q)$, $0\le q\le 1$, $x$ = 0, 0. … Magnify

►

►►

Figure 20.3.7: ${\theta }_2(x,q)$, $0\le q\le 1$, $x$ = 0, 0. … Magnify

►

►►

Figure 20.3.8: ${\theta }_3(x,q)$, $0\le q\le 1$, $x$ = 0, 0. … Magnify

►

►►

Figure 20.3.9: ${\theta }_4(x,q)$, $0\le q\le 1$, $x$ = 0, 0. … Magnify

… ►

►

►

Figure 20.3.14: ${\theta }_1(\pi x+\mathrm{i}y,0.12)$, $-1\le x\le 1$, $-1\le y\le 2.3$. Magnify 3D Help

…