Struve functions and modified Struve functions

SearchAdvancedHelp

(0.006 seconds)

1—10 of 18 matching pages

1: 11.12 Physical Applications

§11.12 Physical Applications

… ►

2: 11.8 Analogs to Kelvin Functions

§11.8 Analogs to Kelvin Functions

…

3: 11.3 Graphics

… ►

►►

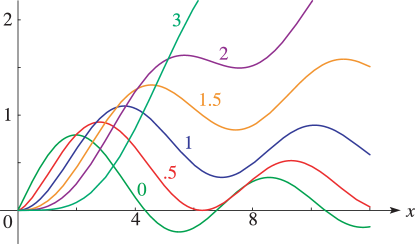
Figure 11.3.1: ${𝐇}_{\nu }\left(x\right)$ for $0\le x\le 12$ and $\nu =0,\frac{1}{2},1,\frac{3}{2},2,3$. Magnify

►

►►

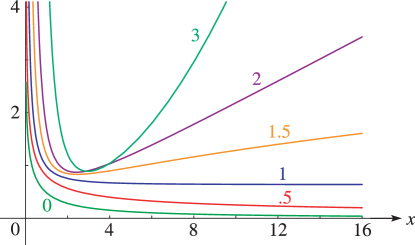
Figure 11.3.2: ${𝐊}_{\nu }\left(x\right)$ for and $\nu =0,\frac{1}{2},1,\frac{3}{2},2,3$. Magnify

►

►►

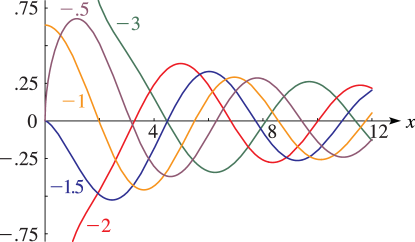
Figure 11.3.3: ${𝐇}_{\nu }\left(x\right)$ for $0\le x\le 12$ and $\nu =-3,-2,-\frac{3}{2},-1,-\frac{1}{2}$. Magnify

►

►►

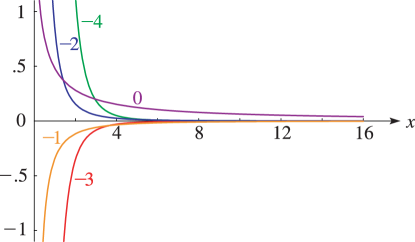
Figure 11.3.4: ${𝐊}_{\nu }\left(x\right)$ for and $\nu =-4,-3,-2,-1,0$. … Magnify

►

►

►

Figure 11.3.5: ${𝐇}_{\nu }\left(x\right)$ for $0\le x\le 8$ and $-4\le \nu \le 4$. Magnify 3D Help

…

4: 11.1 Special Notation

§11.1 Special Notation

… ►For the functions $J_{\nu }\left(z\right)$, $Y_{\nu }\left(z\right)$, $H_{\nu }^{(1)}\left(z\right)$, $H_{\nu }^{(2)}\left(z\right)$, $I_{\nu }\left(z\right)$, and $K_{\nu }\left(z\right)$ see §§10.2(ii), 10.25(ii). ►The functions treated in this chapter are the Struve functions ${𝐇}_{\nu }\left(z\right)$ and ${𝐊}_{\nu }\left(z\right)$, the modified Struve functions ${𝐋}_{\nu }\left(z\right)$ and ${𝐌}_{\nu }\left(z\right)$, the Lommel functions $s_{\mu ,\nu }\left(z\right)$ and $S_{\mu ,\nu }\left(z\right)$, the Anger function ${𝐉}_{\nu }\left(z\right)$, the Weber function ${𝐄}_{\nu }\left(z\right)$, and the associated Anger–Weber function ${𝐀}_{\nu }\left(z\right)$.

5: 11.7 Integrals and Sums

… ►

§11.7(i) Indefinite Integrals

… ►

§11.7(ii) Definite Integrals

… ► ►

§11.7(iii) Laplace Transforms

… ►

§11.7(v) Compendia

…

6: 11.2 Definitions

§11.2 Definitions

►

§11.2(i) Power-Series Expansions

… ► … ►Particular solutions: … ►Particular solutions: …

7: 11.14 Tables

… ►

§11.14(ii) Struve Functions

… ►

§11.14(iii) Integrals

… ►

§11.14(v) Incomplete Functions

…

8: 11.4 Basic Properties

… ►

§11.4(i) Half-Integer Orders

… ►

§11.4(ii) Inequalities

… ►

§11.4(iii) Analytic Continuation

… ►

§11.4(v) Recurrence Relations and Derivatives

… ►

§11.4(vii) Zeros

…

9: 11.15 Approximations

… ►

§11.15(i) Expansions in Chebyshev Series

…

10: 11.5 Integral Representations

… ►

§11.5(i) Integrals Along the Real Line

… ►

11.5.4 $${𝐌}_{\nu }\left(z\right)=-\frac{2{(\frac{1}{2}z)}^{\nu }}{\sqrt{\pi }\mathrm{\Gamma }\left(\nu +\frac{1}{2}\right)}{\int }_0^1{\mathrm{e}}^{-zt}{(1-t^2)}^{\nu -\frac{1}{2}}dt,$$ $\mathrm{\Re }\nu >-\frac{1}{2}$,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${𝐌}_{\nu }\left(z\right)$: modified Struve function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $\mathrm{\Re }$: real part, $z$: complex variable and $\nu$: real or complex order

Referenced by:

§11.5(i), §11.5(ii), §11.6(i), §11.6(iii)

Permalink:

http://dlmf.nist.gov/11.5.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §11.5(i), §11.5 and Ch.11

… ►

§11.5(ii) Contour Integrals

… ►

Mellin–Barnes Integrals

… ►

§11.5(iii) Compendia

…