Riemann%E2%80%93Siegel%20formula

SearchAdvancedHelp

(0.002 seconds)

1—10 of 351 matching pages

1: 21.7 Riemann Surfaces

§21.7 Riemann Surfaces

►

§21.7(i) Connection of Riemann Theta Functions to Riemann Surfaces

►In almost all applications, a Riemann theta function is associated with a compact Riemann surface. … ►is a Riemann matrix and it is used to define the corresponding Riemann theta function. … ►

§21.7(iii) Frobenius’ Identity

…

2: 25.1 Special Notation

… ► ►►

$k,m,n$	nonnegative integers.
…

►The main function treated in this chapter is the Riemann zeta function $\zeta \left(s\right)$. This notation was introduced in Riemann (1859). ►The main related functions are the Hurwitz zeta function $\zeta (s,a)$, the dilogarithm ${\mathrm{Li}}_2\left(z\right)$, the polylogarithm ${\mathrm{Li}}_s\left(z\right)$ (also known as Jonquière’s function $\varphi (z,s)$), Lerch’s transcendent $\mathrm{\Phi }(z,s,a)$, and the Dirichlet $L$-functions $L(s,\chi )$.

3: 21.2 Definitions

… ►

§21.2(i) Riemann Theta Functions

… ►For numerical purposes we use the scaled Riemann theta function $\widehat{\theta }\left(𝐳\right|𝛀)$, defined by (Deconinck et al. (2004)), …Many applications involve quotients of Riemann theta functions: the exponential factor then disappears. … ►

§21.2(ii) Riemann Theta Functions with Characteristics

… ►It is a translation of the Riemann theta function (21.2.1), multiplied by an exponential factor: …

4: 25.10 Zeros

… ► … ►

§25.10(ii) Riemann–Siegel Formula

… ►Sign changes of $Z(t)$ are determined by multiplying (25.9.3) by $\exp \left(\mathrm{i}\vartheta (t)\right)$ to obtain the Riemann–Siegel formula: … ►Calculations based on the Riemann–Siegel formula reveal that the first ten billion zeros of $\zeta \left(s\right)$ in the critical strip are on the critical line (van de Lune et al. (1986)). … ►For further information on the Riemann–Siegel expansion see Berry (1995).

5: 25.20 Approximations

… ►

Cody et al. (1971) gives rational approximations for $\zeta \left(s\right)$ in the form of quotients of polynomials or quotients of Chebyshev series. The ranges covered are $0.5\le s\le 5$, $5\le s\le 11$, $11\le s\le 25$, $25\le s\le 55$. Precision is varied, with a maximum of 20S.

►

Piessens and Branders (1972) gives the coefficients of the Chebyshev-series expansions of $s\zeta \left(s+1\right)$ and $\zeta \left(s+k\right)$, $k=2,3,4,5,8$, for $0\le s\le 1$ (23D).

►

Luke (1969b, p. 306) gives coefficients in Chebyshev-series expansions that cover $\zeta \left(s\right)$ for $0\le s\le 1$ (15D), $\zeta \left(s+1\right)$ for $0\le s\le 1$ (20D), and $\ln \xi \left(\frac{1}{2}+\mathrm{i}x\right)$ (§25.4) for $-1\le x\le 1$ (20D). For errata see Piessens and Branders (1972).

… ►

Antia (1993) gives minimax rational approximations for $\mathrm{\Gamma }\left(s+1\right)F_s(x)$, where $F_s(x)$ is the Fermi–Dirac integral (25.12.14), for the intervals and , with $s=-\frac{1}{2},\frac{1}{2},\frac{3}{2},\frac{5}{2}$. For each $s$ there are three sets of approximations, with relative maximum errors ${10}^{-4},{10}^{-8},{10}^{-12}$.

6: 25.18 Methods of Computation

… ►

§25.18(i) Function Values and Derivatives

►The principal tools for computing $\zeta \left(s\right)$ are the expansion (25.2.9) for general values of $s$, and the Riemann–Siegel formula (25.10.3) (extended to higher terms) for $\zeta \left(\frac{1}{2}+\mathrm{i}t\right)$. …Calculations relating to derivatives of $\zeta \left(s\right)$ and/or $\zeta (s,a)$ can be found in Apostol (1985a), Choudhury (1995), Miller and Adamchik (1998), and Yeremin et al. (1988). … ►

§25.18(ii) Zeros

►Most numerical calculations of the Riemann zeta function are concerned with locating zeros of $\zeta \left(\frac{1}{2}+\mathrm{i}t\right)$ in an effort to prove or disprove the Riemann hypothesis, which states that all nontrivial zeros of $\zeta \left(s\right)$ lie on the critical line $\mathrm{\Re }s=\frac{1}{2}$. …

7: 21.6 Products

§21.6 Products

►

§21.6(i) Riemann Identity

… ►Then …This is the Riemann identity. … ►

§21.6(ii) Addition Formulas

…

8: 25.4 Reflection Formulas

§25.4 Reflection Formulas

… ►

25.4.1 $$\zeta \left(1-s\right)=2{(2\pi )}^{-s}\cos \left(\frac{1}{2}\pi s\right)\mathrm{\Gamma }\left(s\right)\zeta \left(s\right),$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\zeta \left(s\right)$: Riemann zeta function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function and $s$: complex variable

Keywords:

reflection formula

Source:

Apostol (1976, (12), p. 259)

Referenced by:

§25.10(i), §5.17

Permalink:

http://dlmf.nist.gov/25.4.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §25.4 and Ch.25

►

25.4.2 $$\zeta \left(s\right)=2{(2\pi )}^{s-1}\sin \left(\frac{1}{2}\pi s\right)\mathrm{\Gamma }\left(1-s\right)\zeta \left(1-s\right).$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\zeta \left(s\right)$: Riemann zeta function, $\pi$: the ratio of the circumference of a circle to its diameter, $\sin z$: sine function and $s$: complex variable

Keywords:

reflection formula

Source:

Apostol (1976, (13), p. 259)

A&S Ref:

23.2.6

Permalink:

http://dlmf.nist.gov/25.4.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §25.4 and Ch.25

… ►

25.4.3 $$\xi \left(s\right)=\xi \left(1-s\right),$$

ⓘ

Symbols:

$\xi \left(s\right)$: Riemann’s $\xi$-function and $s$: complex variable

Keywords:

reflection formula

Source:

Apostol (1976, p. 260)

Permalink:

http://dlmf.nist.gov/25.4.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §25.4 and Ch.25

►where $\xi \left(s\right)$ is Riemann’s $\xi$-function, defined by: …

9: 25.3 Graphics

§25.3 Graphics

►

►►

Figure 25.3.1: Riemann zeta function $\zeta \left(x\right)$ and its derivative ${\zeta }^{\prime }\left(x\right)$, $-20\le x\le 10$. Magnify

►

►►

Figure 25.3.2: Riemann zeta function $\zeta \left(x\right)$ and its derivative ${\zeta }^{\prime }\left(x\right)$, $-12\le x\le -2$. Magnify

… ►

►►

Figure 25.3.4: $Z(t)$, $0\le t\le 50$. $Z(t)$ and $\zeta \left(\frac{1}{2}+\mathrm{i}t\right)$ have the same zeros. … Magnify

… ►

►►

Figure 25.3.6: $Z(t)$, $10000\le t\le 10050$. Magnify

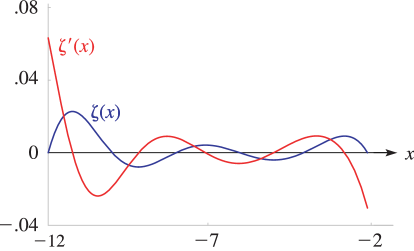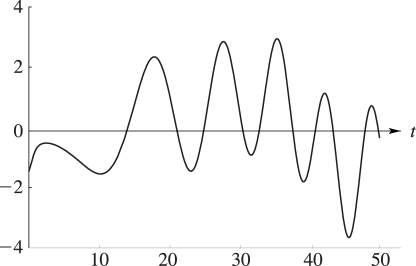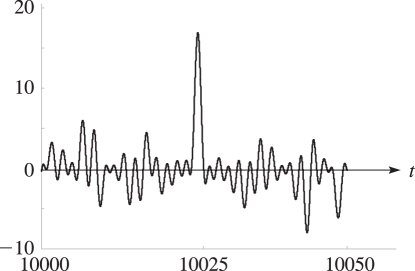10: 21.10 Methods of Computation

… ►

§21.10(i) General Riemann Theta Functions

… ►

§21.10(ii) Riemann Theta Functions Associated with a Riemann Surface

… ►

Belokolos et al. (1994, Chapter 5) and references therein. Here the Riemann surface is represented by the action of a Schottky group on a region of the complex plane. The same representation is used in Gianni et al. (1998).

►

Tretkoff and Tretkoff (1984). Here a Hurwitz system is chosen to represent the Riemann surface.

►

Deconinck and van Hoeij (2001). Here a plane algebraic curve representation of the Riemann surface is used.