Mathieu equation

SearchAdvancedHelp

(0.004 seconds)

1—10 of 54 matching pages

1: 28.2 Definitions and Basic Properties

… ►

§28.2(i) Mathieu’s Equation

… ►

28.2.1 $$w^{\prime \prime }+(a-2q\cos \left(2z\right))w=0.$$

ⓘ

Symbols:

$\cos z$: cosine function, $q=h^2$: parameter, $z$: complex variable, $a$: parameter and $w(z)$: Mathieu’s equation solution

A&S Ref:

20.3.1 20.1.1 (in slightly different form)

Referenced by:

§1.18(vii), Figure 28.17.1, Figure 28.17.1, §28.17, §28.17, §28.2(ii), §28.2(ii), §28.2(iii), §28.2(iv), §28.20(i), §28.29(i), §28.32(i), §28.32(i), 1st item, 2nd item, §28.33(iii), item (a), item (c), item (c), §28.5(i), §28.8(iv), §28.8(iv), §28.8(iv), §30.2(iii)

Permalink:

http://dlmf.nist.gov/28.2.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §28.2(i), §28.2 and Ch.28

… ►

§28.2(iii) Floquet’s Theorem and the Characteristic Exponents

… ►This is the characteristic equation of Mathieu’s equation (28.2.1). … ►

§28.2(iv) Floquet Solutions

…

2: 28.20 Definitions and Basic Properties

… ►

§28.20(i) Modified Mathieu’s Equation

►When $z$ is replaced by $\pm \mathrm{i}z$, (28.2.1) becomes the modified Mathieu’s equation: ►

28.20.1 $$w^{\prime \prime }-\left(a-2q\cosh \left(2z\right)\right)w=0,$$

ⓘ

Symbols:

$\cosh z$: hyperbolic cosine function, $q=h^2$: parameter, $z$: complex variable, $a$: parameter and $w(z)$: Mathieu’s equation solution

A&S Ref:

20.1.2 (in slightly different form) 20.8.6

Referenced by:

§28.20(iii), §28.32(i), 1st item, 2nd item, item (b), §28.8(iv), §28.8(iv)

Permalink:

http://dlmf.nist.gov/28.20.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §28.20(i), §28.20 and Ch.28

… ►

28.20.2 $$({\zeta }^2-1)w^{\prime \prime }+\zeta w^{\prime }+\left(4q{\zeta }^2-2q-a\right)w=0,$$ $\zeta =\cosh z$.

ⓘ

Symbols:

$\cosh z$: hyperbolic cosine function, $q=h^2$: parameter, $z$: complex variable, $a$: parameter and $w(z)$: Mathieu’s equation solution

Referenced by:

§28.20(iii)

Permalink:

http://dlmf.nist.gov/28.20.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §28.20(i), §28.20 and Ch.28

… ►

28.20.6 $${\mathrm{Fe}}_n(z,q)=\mp \mathrm{i}{\mathrm{fe}}_n(\pm \mathrm{i}z,q),$$ $n=0,1,\mathrm{\dots }$,

ⓘ

Defines:

${\mathrm{Fe}}_n(z,q)$: modified Mathieu function

Symbols:

${\mathrm{fe}}_n(z,q)$: second solution, Mathieu’s equation, $\mathrm{i}$: imaginary unit, $q=h^2$: parameter, $n$: integer and $z$: complex variable

A&S Ref:

20.6.1 (in slightly different form) 20.6.2 (in slightly different form)

Permalink:

http://dlmf.nist.gov/28.20.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §28.20(ii), §28.20 and Ch.28

…

3: 28.17 Stability as $x\to \pm \mathrm{\infty }$

§28.17 Stability as $x\to \pm \mathrm{\infty }$

… ► ►

►►

Figure 28.17.1: Stability chart for eigenvalues of Mathieu’s equation (28.2.1). Magnify

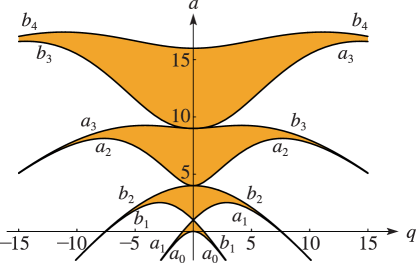4: 28.7 Analytic Continuation of Eigenvalues

§28.7 Analytic Continuation of Eigenvalues

… ►The normal values are simple roots of the corresponding equations (28.2.21) and (28.2.22). … ► … ►

28.7.1 $$\sum _{n=0}^{\mathrm{\infty }}\left(a_{2n}\left(q\right)-{(2n)}^2\right)=0,$$

ⓘ

Symbols:

$a_n\left(q\right)$: eigenvalues of Mathieu equation, $q=h^2$: parameter and $n$: integer

Permalink:

http://dlmf.nist.gov/28.7.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §28.7 and Ch.28

… ►

28.7.4 $$\sum _{n=0}^{\mathrm{\infty }}\left(b_{2n+2}\left(q\right)-{(2n+2)}^2\right)=0.$$

ⓘ

Symbols:

$b_n\left(q\right)$: eigenvalues of Mathieu equation, $q=h^2$: parameter and $n$: integer

Permalink:

http://dlmf.nist.gov/28.7.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §28.7 and Ch.28

5: 28.6 Expansions for Small $q$

… ►

§28.6(i) Eigenvalues

… ►

28.6.14 $$\begin{array}{c}{a}_m\left(q\right)\\ b_m\left(q\right)\end{array}\}=m^2+\frac{1}{2(m^2-1)}{q}^2+\frac{5m^2+7}{32{(m^2-1)}^3(m^2-4)}{q}^4+\frac{9m^4+58m^2+29}{64{(m^2-1)}^5(m^2-4)(m^2-9)}{q}^6+\mathrm{\cdots }.$$

ⓘ

Symbols:

$a_n\left(q\right)$: eigenvalues of Mathieu equation, $b_n\left(q\right)$: eigenvalues of Mathieu equation, $m$: integer and $q=h^2$: parameter

A&S Ref:

20.2.26

Referenced by:

§28.6(i), §28.6(i), Erratum (V1.1.10) for Sections 28.6(i), 28.6(ii), 28.8(i), 28.8(ii)

Permalink:

http://dlmf.nist.gov/28.6.E14

Encodings:

pMML, png, TeX

See also:

Annotations for §28.6(i), §28.6 and Ch.28

… ►

28.6.15 $$a_m\left(q\right)-b_m\left(q\right)=\frac{2q^m}{{\left(2^{m-1}(m-1)!\right)}^2}\left(1+O\left(q^2\right)\right).$$

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $a_n\left(q\right)$: eigenvalues of Mathieu equation, $b_n\left(q\right)$: eigenvalues of Mathieu equation, $!$: factorial (as in $n!$), $m$: integer and $q=h^2$: parameter

Permalink:

http://dlmf.nist.gov/28.6.E15

Encodings:

pMML, png, TeX

See also:

Annotations for §28.6(i), §28.6 and Ch.28

►Higher coefficients in the foregoing series can be found by equating coefficients in the following continued-fraction equations: … ►

Table 28.6.1: Radii of convergence for power-series expansions of eigenvalues of Mathieu’s equation.

► ►►

$n$	${\rho }_n^{(1)}$		${\rho }_n^{(2)}$		${\rho }_n^{(3)}$
…

►

…

6: 28.13 Graphics

… ►

§28.13(i) Eigenvalues ${\lambda }_{\nu }\left(q\right)$ for General $\nu$

…

7: 28.5 Second Solutions ${\mathrm{fe}}_n$, ${\mathrm{ge}}_n$

… ►

§28.5(i) Definitions

… ► … ► … ► ►

§28.5(ii) Graphics: Line Graphs of Second Solutions of Mathieu’s Equation

…

8: 28.12 Definitions and Basic Properties

… ►

§28.12(i) Eigenvalues ${\lambda }_{\nu +2n}\left(q\right)$

… ►For given $\nu$ (or $\cos \left(\nu \pi \right)$) and $q$, equation (28.2.16) determines an infinite discrete set of values of $a$, denoted by ${\lambda }_{\nu +2n}\left(q\right)$, $n=0,\pm 1,\pm 2,\mathrm{\dots }$. … … ►

28.12.3

ⓘ

Symbols:

$a_n\left(q\right)$: eigenvalues of Mathieu equation, $b_n\left(q\right)$: eigenvalues of Mathieu equation, ${\lambda }_{\nu +2n}\left(q\right)$: eigenvalues of Mathieu equation, $m$: integer and $q=h^2$: parameter

Referenced by:

§28.12(ii)

Permalink:

http://dlmf.nist.gov/28.12.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §28.12(i), §28.12 and Ch.28

… ►They have the following pseudoperiodic and orthogonality properties: …

9: 28.16 Asymptotic Expansions for Large $q$

§28.16 Asymptotic Expansions for Large $q$

… ►

28.16.1 $${\lambda }_{\nu }\left(h^2\right)\sim -2h^2+2sh-\frac{1}{8}(s^2+1)-\frac{1}{2^{7}h}(s^3+3s)-\frac{1}{2^{12}{h}^2}(5s^4+34s^2+9)-\frac{1}{2^{17}{h}^3}(33s^5+410s^3+405s)-\frac{1}{2^{20}{h}^4}(63s^6+1260s^4+2943s^2+486)-\frac{1}{2^{25}{h}^5}(527s^7+15617s^5+69001s^3+41607s)+\mathrm{\cdots }.$$

ⓘ

Symbols:

${\lambda }_{\nu +2n}\left(q\right)$: eigenvalues of Mathieu equation, $\sim$: Poincaré asymptotic expansion, $h$: parameter and $\nu$: complex parameter

Permalink:

http://dlmf.nist.gov/28.16.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §28.16 and Ch.28

…

10: 28 Mathieu Functions and Hill’s Equation

Chapter 28 Mathieu Functions and Hill’s Equation

…