Kelvin ship-wave pattern

SearchAdvancedHelp

(0.004 seconds)

1—10 of 36 matching pages

1: 36.13 Kelvin’s Ship-Wave Pattern

§36.13 Kelvin’s Ship-Wave Pattern

… ►

►►

Figure 36.13.1: Kelvin’s ship wave pattern, computed from the uniform asymptotic approximation (36.13.8), as a function of $x=\rho \cos \varphi$, $y=\rho \sin \varphi$. Magnify

►For further information see Lord Kelvin (1891, 1905) and Ursell (1960, 1994).

2: Bibliography U

… ►

On Kelvin’s ship-wave pattern. J. Fluid Mech. 8 (3), pp. 418–431.

ⓘ

External Links:

Document, MathReview (R. C. MacCamy), ZentralBlatt

Referenced by:

§36.13.

Encodings:

BibTeX

…

3: Bibliography L

… ►

Popular Lectures and Addresses. Vol. 3, pp. 481–488.

ⓘ

Referenced by:

§36.13.

Encodings:

BibTeX

►

Deep water ship-waves. Phil. Mag. 9, pp. 733–757.

ⓘ

External Links:

ZentralBlatt

Referenced by:

§36.13.

Encodings:

BibTeX

…

4: 10.62 Graphs

§10.62 Graphs

… ►

►►

Figure 10.62.1: $\mathrm{ber}x$, $\mathrm{bei}x$, ${\mathrm{ber}}^{\prime }x$, ${\mathrm{bei}}^{\prime }x$, $0\le x\le 8$. Magnify

►

►►

Figure 10.62.2: $\ker x$, $\mathrm{kei}x$, ${\ker }^{\prime }x$, ${\mathrm{kei}}^{\prime }x$, $0\le x\le 8$. Magnify

►

►►

Figure 10.62.3: ${\mathrm{e}}^{-x/\sqrt{2}}\mathrm{ber}x$, ${\mathrm{e}}^{-x/\sqrt{2}}\mathrm{bei}x$, ${\mathrm{e}}^{-x/\sqrt{2}}M\left(x\right)$, $0\le x\le 8$. Magnify

►

►►

Figure 10.62.4: ${\mathrm{e}}^{x/\sqrt{2}}\ker x$, ${\mathrm{e}}^{x/\sqrt{2}}\mathrm{kei}x$, ${\mathrm{e}}^{x/\sqrt{2}}N\left(x\right)$, $0\le x\le 8$. Magnify

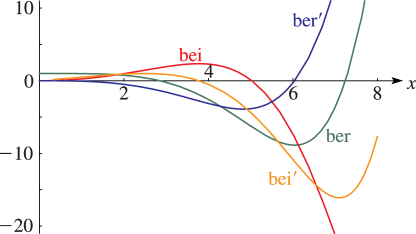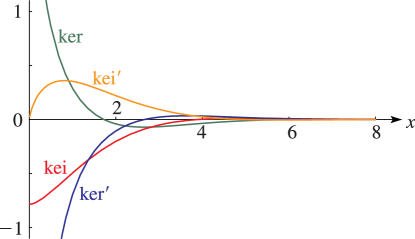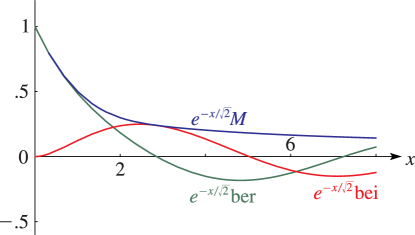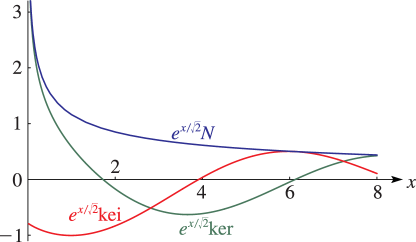5: 10.61 Definitions and Basic Properties

… ►

§10.61(i) Definitions

… ►When $\nu =0$ suffices on $\mathrm{ber}$, $\mathrm{bei}$, $\ker$, and $\mathrm{kei}$ are usually suppressed. … ►

§10.61(ii) Differential Equations

… ►

§10.61(iii) Reflection Formulas for Arguments

… ►

§10.61(iv) Reflection Formulas for Orders

…

6: 10.64 Integral Representations

§10.64 Integral Representations

►

Schläfli-Type Integrals

… ►

10.64.2 $${\mathrm{bei}}_n\left(x\sqrt{2}\right)=\frac{{(-1)}^n}{\pi }{\int }_0^{\pi }\sin \left(x\sin t-nt\right)\sinh \left(x\sin t\right)dt.$$

ⓘ

Symbols:

${\mathrm{bei}}_{\nu }\left(x\right)$: Kelvin function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\sinh z$: hyperbolic sine function, $\int$: integral, $\sin z$: sine function, $n$: integer and $x$: real variable

Permalink:

http://dlmf.nist.gov/10.64.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §10.64, §10.64 and Ch.10

►See Apelblat (1991) for these results, and also for similar representations for ${\mathrm{ber}}_{\nu }\left(x\sqrt{2}\right)$, ${\mathrm{bei}}_{\nu }\left(x\sqrt{2}\right)$, and their $\nu$-derivatives.

7: 10.63 Recurrence Relations and Derivatives

… ►

§10.63(i) ${\mathrm{ber}}_{\nu }x$, ${\mathrm{bei}}_{\nu }x$, ${\ker }_{\nu }x$, ${\mathrm{kei}}_{\nu }x$

►Let $f_{\nu }(x)$, $g_{\nu }(x)$ denote any one of the ordered pairs: … ►

§10.63(ii) Cross-Products

… ►Equations (10.63.6) and (10.63.7) also hold when the symbols $\mathrm{ber}$ and $\mathrm{bei}$ in (10.63.5) are replaced throughout by $\ker$ and $\mathrm{kei}$, respectively.

8: 10.67 Asymptotic Expansions for Large Argument

… ►

§10.67(i) ${\mathrm{ber}}_{\nu }x,{\mathrm{bei}}_{\nu }x,{\ker }_{\nu }x,{\mathrm{kei}}_{\nu }x$, and Derivatives

… ►The contributions of the terms in ${\ker }_{\nu }x$, ${\mathrm{kei}}_{\nu }x$, ${\ker }_{\nu }^{\prime }x$, and ${\mathrm{kei}}_{\nu }^{\prime }x$ on the right-hand sides of (10.67.3), (10.67.4), (10.67.7), and (10.67.8) are exponentially small compared with the other terms, and hence can be neglected in the sense of Poincaré asymptotic expansions (§2.1(iii)). … ►

§10.67(ii) Cross-Products and Sums of Squares in the Case $\nu =0$

… ►

10.67.10 $$\mathrm{ber}x{\mathrm{bei}}^{\prime }x-{\mathrm{ber}}^{\prime }x\mathrm{bei}x\sim \frac{{\mathrm{e}}^{x\sqrt{2}}}{2\pi x}\left(\frac{1}{\sqrt{2}}+\frac{1}{8}\frac{1}{x}+\frac{9}{64\sqrt{2}}\frac{1}{x^2}+\frac{39}{512}\frac{1}{x^3}+\frac{75}{8192\sqrt{2}}\frac{1}{x^4}+\mathrm{\cdots }\right),$$

ⓘ

Symbols:

${\mathrm{bei}}_{\nu }\left(x\right)$: Kelvin function, ${\mathrm{ber}}_{\nu }\left(x\right)$: Kelvin function, $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm and $x$: real variable

A&S Ref:

9.10.28

Permalink:

http://dlmf.nist.gov/10.67.E10

Encodings:

pMML, png, TeX

See also:

Annotations for §10.67(ii), §10.67 and Ch.10

…

9: 10.65 Power Series

§10.65 Power Series

►

§10.65(i) ${\mathrm{ber}}_{\nu }x$ and ${\mathrm{bei}}_{\nu }x$

… ►

§10.65(ii) ${\ker }_{\nu }x$ and ${\mathrm{kei}}_{\nu }x$

… ►

§10.65(iv) Compendia

►For further power series summable in terms of Kelvin functions and their derivatives see Hansen (1975).

10: 10.70 Zeros

§10.70 Zeros

… ►

$$\text{zeros of }{\mathrm{ber}}_{\nu }x\sim \sqrt{2}(t-f(t)),$$ $t=(m-\frac{1}{2}\nu -\frac{3}{8})\pi$,

►

$$\text{zeros of }{\mathrm{bei}}_{\nu }x\sim \sqrt{2}(t-f(t)),$$ $t=(m-\frac{1}{2}\nu +\frac{1}{8})\pi$,

►

$$\text{zeros of }{\ker }_{\nu }x\sim \sqrt{2}(t+f(-t)),$$ $t=(m-\frac{1}{2}\nu -\frac{5}{8})\pi$,

►

$$\text{zeros of }{\mathrm{kei}}_{\nu }x\sim \sqrt{2}(t+f(-t)),$$ $t=(m-\frac{1}{2}\nu -\frac{1}{8})\pi$.

…