Jacobi polynomials

SearchAdvancedHelp

(0.006 seconds)

11—20 of 70 matching pages

11: 18.37 Classical OP’s in Two or More Variables

… ►

Definition in Terms of Jacobi Polynomials

►

18.37.1 $$R_{m,n}^{(\alpha )}\left(r{\mathrm{e}}^{\mathrm{i}\theta }\right)={\mathrm{e}}^{\mathrm{i}(m-n)\theta }{r}^{|m-n|}\frac{P_{\min (m,n)}^{(\alpha ,|m-n|)}\left(2r^2-1\right)}{P_{\min (m,n)}^{(\alpha ,|m-n|)}\left(1\right)},$$ $r\ge 0$, $\theta \in ℝ$, $\alpha >-1$.

ⓘ

Defines:

$R_{m,n}^{(\alpha )}\left(z\right)$: disk polynomial

Symbols:

$P_n^{(\alpha ,\beta )}\left(x\right)$: Jacobi polynomial, $\in$: element of, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $ℝ$: real line, $z$: complex variable, $m$: nonnegative integer and $n$: nonnegative integer

Referenced by:

§18.37(ii)

Permalink:

http://dlmf.nist.gov/18.37.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §18.37(i), §18.37(i), §18.37 and Ch.18

… ►

Definition in Terms of Jacobi Polynomials

►

18.37.7 $$P_{m,n}^{\alpha ,\beta ,\gamma }(x,y)=P_{m-n}^{(\alpha ,\beta +\gamma +2n+1)}\left(2x-1\right)x^n{P}_n^{(\beta ,\gamma )}\left(2x^{-1}y-1\right),$$ $m\ge n\ge 0$, $\alpha ,\beta ,\gamma >-1$.

ⓘ

Defines:

$P_{m,n}^{\alpha ,\beta ,\gamma }(x,y)$: triangle polynomial

Symbols:

$P_n^{(\alpha ,\beta )}\left(x\right)$: Jacobi polynomial, $y$: real variable, $m$: nonnegative integer, $n$: nonnegative integer and $x$: real variable

Referenced by:

§18.37(ii)

Permalink:

http://dlmf.nist.gov/18.37.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §18.37(ii), §18.37(ii), §18.37 and Ch.18

… ►In several variables they occur, for $q=1$, as Jack polynomials and also as Jacobi polynomials associated with root systems; see Macdonald (1995, Chapter VI, §10), Stanley (1989), Kuznetsov and Sahi (2006, Part 1), Heckman (1991). …

12: 18.18 Sums

… ►

18.18.2 $$f(z)=\sum _{n=0}^{\mathrm{\infty }}{a}_n{P}_n^{(\alpha ,\beta )}\left(z\right),$$

ⓘ

Symbols:

$P_n^{(\alpha ,\beta )}\left(x\right)$: Jacobi polynomial, $z$: complex variable, $n$: nonnegative integer, $f(z)$: analytic function and $a_n$

Referenced by:

§18.18(i), §18.18(i), §18.18(i), §18.18(i)

Permalink:

http://dlmf.nist.gov/18.18.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §18.18(i), §18.18(i), §18.18 and Ch.18

… ►See Andrews et al. (1999, Lemma 7.1.1) for the more general expansion of $P_n^{(\gamma ,\delta )}\left(x\right)$ in terms of $P_n^{(\alpha ,\beta )}\left(x\right)$. … ►

Jacobi

… ►

18.18.25 $$\frac{P_n^{(\alpha ,\beta )}\left(x\right)}{P_n^{(\alpha ,\beta )}\left(1\right)}\frac{P_n^{(\alpha ,\beta )}\left(y\right)}{P_n^{(\alpha ,\beta )}\left(1\right)}=\sum _{\mathrm{\ell }=0}^n{b}_{n,\mathrm{\ell }}{(x+y)}^{\mathrm{\ell }}\frac{P_{\mathrm{\ell }}^{(\alpha ,\beta )}\left((1+xy)/(x+y)\right)}{P_{\mathrm{\ell }}^{(\alpha ,\beta )}\left(1\right)},$$

ⓘ

Symbols:

$P_n^{(\alpha ,\beta )}\left(x\right)$: Jacobi polynomial, $y$: real variable, $\mathrm{\ell }$: nonnegative integer, $n$: nonnegative integer and $x$: real variable

Permalink:

http://dlmf.nist.gov/18.18.E25

Encodings:

pMML, png, TeX

See also:

Annotations for §18.18(vi), §18.18(vi), §18.18 and Ch.18

►

18.18.26 $$\frac{P_n^{(\alpha ,\beta )}\left(x\right)}{P_n^{(\alpha ,\beta )}\left(1\right)}=\sum _{\mathrm{\ell }=0}^n{b}_{n,\mathrm{\ell }}{(x+1)}^{\mathrm{\ell }}.$$

ⓘ

Symbols:

$P_n^{(\alpha ,\beta )}\left(x\right)$: Jacobi polynomial, $\mathrm{\ell }$: nonnegative integer, $n$: nonnegative integer and $x$: real variable

Permalink:

http://dlmf.nist.gov/18.18.E26

Encodings:

pMML, png, TeX

See also:

Annotations for §18.18(vi), §18.18(vi), §18.18 and Ch.18

…

13: 18.11 Relations to Other Functions

… ►

18.11.1 $${𝖯}_n^m\left(x\right)={\left(\frac{1}{2}\right)}_m{(-2)}^m{(1-x^2)}^{\frac{1}{2}m}{C}_{n-m}^{(m+\frac{1}{2})}\left(x\right)={\left(n+1\right)}_m{(-2)}^{-m}{(1-x^2)}^{\frac{1}{2}m}{P}_{n-m}^{(m,m)}\left(x\right),$$ $0\le m\le n$.

ⓘ

Symbols:

: Ferrers function of the first kind, $P_n^{(\alpha ,\beta )}\left(x\right)$: Jacobi polynomial, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $C_n^{(\lambda )}\left(x\right)$: ultraspherical (or Gegenbauer) polynomial, $m$: nonnegative integer, $n$: nonnegative integer and $x$: real variable

Referenced by:

§14.3(iv), §18.11(i)

Permalink:

http://dlmf.nist.gov/18.11.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §18.11(i), §18.11(i), §18.11 and Ch.18

… ►

Jacobi

►

18.11.5 $$\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n^{\alpha }}{P}_n^{(\alpha ,\beta )}\left(1-\frac{z^2}{2n^2}\right)=\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n^{\alpha }}{P}_n^{(\alpha ,\beta )}\left(\cos \frac{z}{n}\right)=\frac{2^{\alpha }}{z^{\alpha }}{J}_{\alpha }\left(z\right).$$

ⓘ

Symbols:

$J_{\nu }\left(z\right)$: Bessel function of the first kind, $P_n^{(\alpha ,\beta )}\left(x\right)$: Jacobi polynomial, $\cos z$: cosine function, $z$: complex variable and $n$: nonnegative integer

A&S Ref:

22.15.1

Referenced by:

§18.11(ii), §18.11(ii)

Permalink:

http://dlmf.nist.gov/18.11.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §18.11(ii), §18.11(ii), §18.11 and Ch.18

…

14: 31.16 Mathematical Applications

… ►Expansions of Heun polynomial products in terms of Jacobi polynomial (§18.3) products are derived in Kalnins and Miller (1991a, b, 1993) from the viewpoint of interrelation between two bases in a Hilbert space: ►

31.16.1 $${\mathrm{𝐻𝑝}}_{n,m}\left(x\right){\mathrm{𝐻𝑝}}_{n,m}\left(y\right)=\sum _{j=0}^n{A}_j{\sin }^{2j}\theta P_{n-j}^{(\gamma +\delta +2j-1,ϵ-1)}\left(\cos \left(2\theta \right)\right)P_j^{(\delta -1,\gamma -1)}\left(\cos \left(2\varphi \right)\right),$$

ⓘ

Symbols:

${\mathrm{𝐻𝑝}}_{n,m}(a,q_{n,m};-n,\beta ,\gamma ,\delta ;z)$: Heun polynomials, $P_n^{(\alpha ,\beta )}\left(x\right)$: Jacobi polynomial, $\cos z$: cosine function, $\sin z$: sine function, $\gamma$: real or complex parameter, $\delta$: real or complex parameter, $ϵ$: real or complex parameter, $j$: nonnegative integer, $m$: nonnegative integer, $n$: nonnegative integer, $a$: complex parameter, $q$: real or complex parameter, $\beta$: real or complex parameter, $\theta$: angle, $\varphi$: angle, $x$: variable, $y$: variable and $A_j$: coefficients

Referenced by:

§31.16(ii), §31.16(ii)

Permalink:

http://dlmf.nist.gov/31.16.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §31.16(ii), §31.16 and Ch.31

…

15: 18.27 $q$-Hahn Class

… ►

18.27.10 $$p_n(x)=P_n^{(\alpha ,\beta )}(x;c,d;q)$$

ⓘ

Symbols:

$P_n^{(\alpha ,\beta )}(x;c,d;q)$: big $q$-Jacobi polynomial, $p_n(x)$: polynomial of degree $n$ , $q$: real variable, $n$: nonnegative integer and $x$: real variable

Permalink:

http://dlmf.nist.gov/18.27.E10

Encodings:

pMML, png, TeX

See also:

Annotations for §18.27(iii), §18.27 and Ch.18

… ►

18.27.12_5 $$\underset{q\to 1}{lim}{P}_n^{(\alpha ,\beta )}(x;c,d;q)={\left(\frac{c+d}{2}\right)}^n{P}_n^{(\alpha ,\beta )}\left(\frac{2x-c+d}{c+d}\right).$$

ⓘ

Symbols:

${}_2{}^{}F_1^{}(a,b;c;z)$: $=F(a,b;c;z)$ notation for Gauss’ hypergeometric function, $P_n^{(\alpha ,\beta )}\left(x\right)$: Jacobi polynomial, $P_n^{(\alpha ,\beta )}(x;c,d;q)$: big $q$-Jacobi polynomial, $q$: real variable, $n$: nonnegative integer and $x$: real variable

Source:

Andrews and Askey (1985, (3.33)); for $c=d=1$

Proof sketch:

On the left substitute first (18.27.6) and next (18.27.5). Then, after taking the limit, a ${}_2{}^{}F_1^{}$ hypergeometric function occurs. Finally use (18.5.7).

Referenced by:

§18.27(iii), §18.27(iii), Erratum (V1.2.0) Section 18.27

Permalink:

http://dlmf.nist.gov/18.27.E12_5

Encodings:

pMML, png, TeX

Addition (effective with 1.2.0):

This equation was added.

See also:

Annotations for §18.27(iii), §18.27(iii), §18.27 and Ch.18

… ►

18.27.14_2 $$\underset{c\to -\mathrm{\infty }}{lim}{P}_n(cqx;a,b,c;q)=p_n(x;a,b;q).$$

ⓘ

Symbols:

$P_n(x;a,b,c;q)$: big $q$-Jacobi polynomial, $p_n(x;a,b;q)$: little $q$-Jacobi polynomial, $q$: real variable, $n$: nonnegative integer and $x$: real variable

Source:

Koekoek et al. (2010, (14.5.14))

Referenced by:

§18.27(iv)

Permalink:

http://dlmf.nist.gov/18.27.E14_2

Encodings:

pMML, png, TeX

See also:

Annotations for §18.27(iv), §18.27(iv), §18.27 and Ch.18

… ►

18.27.14_4 $$\underset{q\to 1}{lim}{p}_n(x;q^{\alpha },q^{\beta };q)=\frac{n!}{{\left(\alpha +1\right)}_n}{P}_n^{(\alpha ,\beta )}\left(1-2x\right).$$

ⓘ

Symbols:

$P_n^{(\alpha ,\beta )}\left(x\right)$: Jacobi polynomial, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $!$: factorial (as in $n!$), $p_n(x;a,b;q)$: little $q$-Jacobi polynomial, $q$: real variable, $n$: nonnegative integer and $x$: real variable

Source:

Koekoek et al. (2010, (14.12.15))

Referenced by:

§18.27(iv)

Permalink:

http://dlmf.nist.gov/18.27.E14_4

Encodings:

pMML, png, TeX

See also:

Annotations for §18.27(iv), §18.27(iv), §18.27 and Ch.18

… ►Little $q$-Jacobi polynomials $p_n(x;a,b;q)$ for $b=0$ are called little $q$-Laguerre or Wall polynomials: …

16: 18.17 Integrals

… ►

Jacobi

… ►

Jacobi

… ►

Jacobi

… ►

Jacobi

… ►

Jacobi

…

17: 18.15 Asymptotic Approximations

… ►

§18.15(i) Jacobi

… ►

18.15.1 $${\left(\sin \frac{1}{2}\theta \right)}^{\alpha +\frac{1}{2}}{\left(\cos \frac{1}{2}\theta \right)}^{\beta +\frac{1}{2}}{P}_n^{(\alpha ,\beta )}\left(\cos \theta \right)={\pi }^{-1}{2}^{2n+\alpha +\beta +1}\mathrm{B}(n+\alpha +1,n+\beta +1)\left(\sum _{m=0}^{M-1}\frac{f_m(\theta )}{2^m{\left(2n+\alpha +\beta +2\right)}_m}+O\left(n^{-M}\right)\right),$$

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $\mathrm{B}(a,b)$: beta function, $P_n^{(\alpha ,\beta )}\left(x\right)$: Jacobi polynomial, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\sin z$: sine function, $m$: nonnegative integer, $n$: nonnegative integer and $f_m(\theta )$

Referenced by:

§18.15(i), §18.15(i)

Permalink:

http://dlmf.nist.gov/18.15.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §18.15(i), §18.15 and Ch.18

… ►For large $\beta$, fixed $\alpha$, and $0\le n/\beta \le c$, Dunster (1999) gives asymptotic expansions of $P_n^{(\alpha ,\beta )}\left(z\right)$ that are uniform in unbounded complex $z$-domains containing $z=\pm 1$. …This reference also supplies asymptotic expansions of $P_n^{(\alpha ,\beta )}\left(z\right)$ for large $n$, fixed $\alpha$, and $0\le \beta /n\le c$. … ►For an asymptotic expansion of $P_n^{(\alpha ,\beta )}\left(z\right)$ as $n\to \mathrm{\infty }$ that holds uniformly for complex $z$ bounded away from $[-1,1]$, see Elliott (1971). …

18: 18.34 Bessel Polynomials

… ►

18.34.8 $$\underset{\alpha \to \mathrm{\infty }}{lim}\frac{P_n^{(\alpha ,a-\alpha -2)}\left(1+\alpha x\right)}{P_n^{(\alpha ,a-\alpha -2)}\left(1\right)}=y_n(x;a).$$

ⓘ

Symbols:

$y_n(x;a)$: Bessel polynomial, $P_n^{(\alpha ,\beta )}\left(x\right)$: Jacobi polynomial, $n$: nonnegative integer and $x$: real variable

Referenced by:

§18.34(iii)

Permalink:

http://dlmf.nist.gov/18.34.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §18.34(iii), §18.34 and Ch.18

►In this limit the finite system of Jacobi polynomials $P_n^{(\alpha ,\beta )}\left(x\right)$ which is orthogonal on $(1,\mathrm{\infty })$ (see §18.3) tends to the finite system of Romanovski–Bessel polynomials which is orthogonal on $(0,\mathrm{\infty })$ (see (18.34.5_5)). …

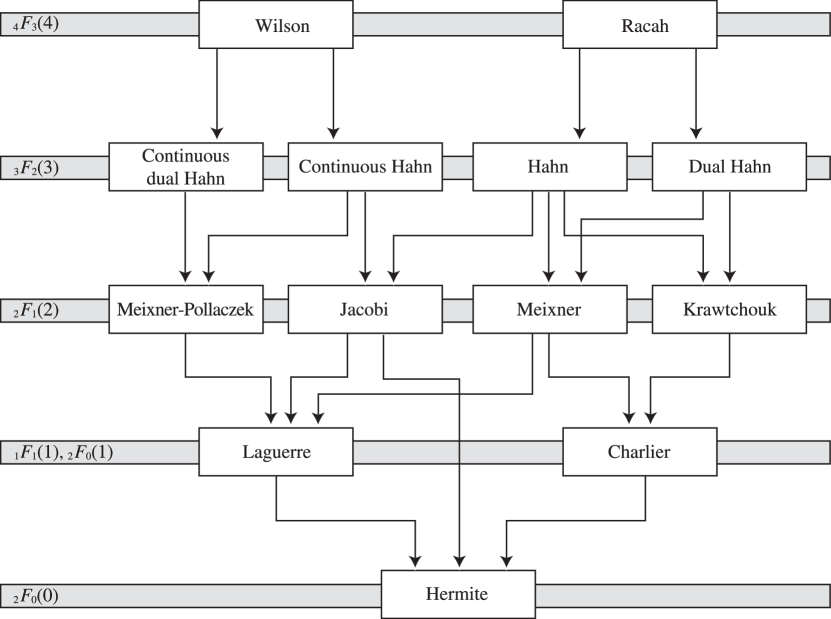
19: 18.21 Hahn Class: Interrelations

… ►

Hahn $\to$ Jacobi

►

18.21.5 $$\underset{N\to \mathrm{\infty }}{lim}{Q}_n(Nx;\alpha ,\beta ,N)=\frac{P_n^{(\alpha ,\beta )}\left(1-2x\right)}{P_n^{(\alpha ,\beta )}\left(1\right)}.$$

ⓘ

Symbols:

$Q_n(x;\alpha ,\beta ,N)$: Hahn polynomial, $P_n^{(\alpha ,\beta )}\left(x\right)$: Jacobi polynomial, $N$: positive integer, $n$: nonnegative integer and $x$: real variable

Referenced by:

§18.21(ii)

Permalink:

http://dlmf.nist.gov/18.21.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §18.21(ii), §18.21(ii), §18.21 and Ch.18

… ►

►►

Figure 18.21.1: Askey scheme. … Magnify

20: 18.5 Explicit Representations

… ►

Table 18.5.1: Classical OP’s: Rodrigues formulas (18.5.5).

► ►►►

$p_n(x)$	$w(x)$	$F(x)$	${\kappa }_n$
$P_n^{(\alpha ,\beta )}\left(x\right)$	${(1-x)}^{\alpha }{(1+x)}^{\beta }$	$1-x^2$	${(-2)}^{n}n!$
…

►

… ►

18.5.7 $$P_n^{(\alpha ,\beta )}\left(x\right)=\sum _{\mathrm{\ell }=0}^n\frac{{\left(n+\alpha +\beta +1\right)}_{\mathrm{\ell }}{\left(\alpha +\mathrm{\ell }+1\right)}_{n-\mathrm{\ell }}}{\mathrm{\ell }!(n-\mathrm{\ell })!}{\left(\frac{x-1}{2}\right)}^{\mathrm{\ell }}=\frac{{\left(\alpha +1\right)}_n}{n!}{}_2{}^{}F_1^{}(\genfrac{}{}{0pt}{}{-n,n+\alpha +\beta +1}{\alpha +1};\frac{1-x}{2}),$$

ⓘ

Symbols:

${}_2{}^{}F_1^{}(a,b;c;z)$: $=F(a,b;c;z)$ notation for Gauss’ hypergeometric function, $P_n^{(\alpha ,\beta )}\left(x\right)$: Jacobi polynomial, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $!$: factorial (as in $n!$), $\mathrm{\ell }$: nonnegative integer, $n$: nonnegative integer and $x$: real variable

A&S Ref:

22.5.42

Referenced by:

§18.17(iv), §18.17(vii), (18.27.12_5), Table 18.3.1, §18.5(iii), §18.5(iii), §18.6(ii), §18.9(iii)

Permalink:

http://dlmf.nist.gov/18.5.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §18.5(iii), §18.5(iii), §18.5 and Ch.18

►

18.5.8 $$P_n^{(\alpha ,\beta )}\left(x\right)=2^{-n}\sum _{\mathrm{\ell }=0}^n\left(\genfrac{}{}{0.0pt}{}{n+\alpha }{\mathrm{\ell }}\right)\left(\genfrac{}{}{0.0pt}{}{n+\beta }{n-\mathrm{\ell }}\right){(x-1)}^{n-\mathrm{\ell }}{(x+1)}^{\mathrm{\ell }}=\frac{{\left(\alpha +1\right)}_n}{n!}{\left(\frac{x+1}{2}\right)}^n{}_2{}^{}F_1^{}(\genfrac{}{}{0pt}{}{-n,-n-\beta }{\alpha +1};\frac{x-1}{x+1}),$$

ⓘ

Symbols:

${}_2{}^{}F_1^{}(a,b;c;z)$: $=F(a,b;c;z)$ notation for Gauss’ hypergeometric function, $P_n^{(\alpha ,\beta )}\left(x\right)$: Jacobi polynomial, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\left(\genfrac{}{}{0.0pt}{}{m}{n}\right)$: binomial coefficient, $!$: factorial (as in $n!$), $\mathrm{\ell }$: nonnegative integer, $n$: nonnegative integer and $x$: real variable

A&S Ref:

22.3.1

Referenced by:

§18.5(iii), §18.5(iii)

Permalink:

http://dlmf.nist.gov/18.5.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §18.5(iii), §18.5(iii), §18.5 and Ch.18

… ►The first of each of equations (18.5.7) and (18.5.8) can be regarded as definitions of $P_n^{(\alpha ,\beta )}\left(x\right)$ when the conditions $\alpha >-1$ and $\beta >-1$ are not satisfied. …For this reason, and also in the interest of simplicity, in the case of the Jacobi polynomials $P_n^{(\alpha ,\beta )}\left(x\right)$ we assume throughout this chapter that $\alpha >-1$ and $\beta >-1$, unless stated otherwise. …