Jacobi nome

SearchAdvancedHelp

(0.003 seconds)

1—10 of 19 matching pages

1: 19.5 Maclaurin and Related Expansions

… ► ►For Jacobi’s nome $q$: ►

19.5.5 $$q=\exp \left(-\pi K^{\prime }\left(k\right)/K\left(k\right)\right)=r+8r^2+84r^3+992r^4+\mathrm{\cdots },$$ $r=\frac{1}{16}{k}^2$, $0\le k\le 1$.

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $K^{\prime }\left(k\right)$: Legendre’s complementary complete elliptic integral of the first kind, $K\left(k\right)$: Legendre’s complete elliptic integral of the first kind, $\exp z$: exponential function, $q$: nome and $k$: real or complex modulus

Referenced by:

§19.5

Permalink:

http://dlmf.nist.gov/19.5.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §19.5 and Ch.19

…

2: 22.2 Definitions

… ►

$k={\displaystyle \frac{{\theta }_2^2(0,q)}{{\theta }_3^2(0,q)}},$

►

$k^{\prime }={\displaystyle \frac{{\theta }_4^2(0,q)}{{\theta }_3^2(0,q)}},$

… ►

22.2.4 $$\mathrm{sn}(z,k)=\frac{{\theta }_3(0,q)}{{\theta }_2(0,q)}\frac{{\theta }_1(\zeta ,q)}{{\theta }_4(\zeta ,q)}=\frac{1}{\mathrm{ns}(z,k)},$$

ⓘ

Defines:

$\mathrm{ns}(z,k)$: Jacobian elliptic function and $\mathrm{sn}(z,k)$: Jacobian elliptic function

Symbols:

${\theta }_j(z,q)$: theta function, $q$: nome, $z$: complex, $k$: modulus and $\zeta$: change of variable

Referenced by:

§23.6(ii)

Permalink:

http://dlmf.nist.gov/22.2.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §22.2 and Ch.22

… ►

22.2.7 $$\mathrm{sd}(z,k)=\frac{{\theta }_3^2(0,q)}{{\theta }_2(0,q){\theta }_4(0,q)}\frac{{\theta }_1(\zeta ,q)}{{\theta }_3(\zeta ,q)}=\frac{1}{\mathrm{ds}(z,k)},$$

ⓘ

Defines:

$\mathrm{ds}(z,k)$: Jacobian elliptic function and $\mathrm{sd}(z,k)$: Jacobian elliptic function

Symbols:

${\theta }_j(z,q)$: theta function, $q$: nome, $z$: complex, $k$: modulus and $\zeta$: change of variable

Permalink:

http://dlmf.nist.gov/22.2.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §22.2 and Ch.22

… ►

22.2.11 $$\mathrm{p}\mathrm{q}(z,k)={\theta }_p\left(z\right|\tau )/{\theta }_q\left(z\right|\tau ),$$

ⓘ

Symbols:

${\theta }_j\left(z\right|\tau )$: theta function, $\mathrm{p}\mathrm{q}(z,k)$: generic Jacobian elliptic function, $q$: nome, $z$: complex, $k$: modulus and $\tau$: ratio

A&S Ref:

16.36.3

Referenced by:

§22.2

Permalink:

http://dlmf.nist.gov/22.2.E11

Encodings:

pMML, png, TeX

See also:

Annotations for §22.2, §22.2 and Ch.22

…

3: 22.16 Related Functions

… ►

22.16.9 $$\mathrm{am}(x,k)=\frac{\pi }{2K}x+2\sum _{n=1}^{\mathrm{\infty }}\frac{q^n\sin \left(2n\zeta \right)}{n(1+q^{2n})}.$$

ⓘ

Symbols:

$\mathrm{am}(x,k)$: Jacobi’s amplitude function, $\pi$: the ratio of the circumference of a circle to its diameter, $K\left(k\right)$: Legendre’s complete elliptic integral of the first kind, $q$: nome, $\sin z$: sine function, $x$: real and $k$: modulus

Referenced by:

§22.20(vi)

Permalink:

http://dlmf.nist.gov/22.16.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §22.16(i), §22.16(i), §22.16 and Ch.22

… ►

22.16.30 $$ℰ(x,k)=\frac{1}{{\theta }_3^2(0,q){\theta }_4(\xi ,q)}\frac{d}{d\xi }{\theta }_4(\xi ,q)+\frac{E\left(k\right)}{K\left(k\right)}x,$$

ⓘ

Symbols:

$ℰ(x,k)$: Jacobi’s epsilon function, ${\theta }_j(z,q)$: theta function, $K\left(k\right)$: Legendre’s complete elliptic integral of the first kind, $E\left(k\right)$: Legendre’s complete elliptic integral of the second kind, $\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $q$: nome, $x$: real and $k$: modulus

Referenced by:

§22.20(vi)

Permalink:

http://dlmf.nist.gov/22.16.E30

Encodings:

pMML, png, TeX

See also:

Annotations for §22.16(ii), §22.16(ii), §22.16 and Ch.22

►where $\xi =x/{\theta }_3^2(0,q)$. …

4: 22.20 Methods of Computation

… ►If either $\tau$ or $q={\mathrm{e}}^{\mathrm{i}\pi \tau }$ is given, then we use $k={\theta }_2^2(0,q)/{\theta }_3^2(0,q)$, $k^{\prime }={\theta }_4^2(0,q)/{\theta }_3^2(0,q)$, $K=\frac{1}{2}\pi {\theta }_3^2(0,q)$, and $K^{\prime }=-\mathrm{i}\tau K$, obtaining the values of the theta functions as in §20.14. …

5: 20.4 Values at $z$ = 0

… ►

20.4.1 $${\theta }_1(0,q)={\theta }_2^{\prime }(0,q)={\theta }_3^{\prime }(0,q)={\theta }_4^{\prime }(0,q)=0,$$

ⓘ

Symbols:

${\theta }_j(z,q)$: theta function and $q$: nome

Permalink:

http://dlmf.nist.gov/20.4.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §20.4(i), §20.4 and Ch.20

… ►

20.4.3 $${\theta }_2(0,q)=2q^{1/4}\prod _{n=1}^{\mathrm{\infty }}\left(1-q^{2n}\right){\left(1+q^{2n}\right)}^2,$$

ⓘ

Symbols:

${\theta }_j(z,q)$: theta function, $n$: integer and $q$: nome

Referenced by:

(20.10.3)

Permalink:

http://dlmf.nist.gov/20.4.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §20.4(i), §20.4 and Ch.20

►

20.4.4 $${\theta }_3(0,q)=\prod _{n=1}^{\mathrm{\infty }}\left(1-q^{2n}\right){\left(1+q^{2n-1}\right)}^2,$$

ⓘ

Symbols:

${\theta }_j(z,q)$: theta function, $n$: integer and $q$: nome

Referenced by:

(20.10.2)

Permalink:

http://dlmf.nist.gov/20.4.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §20.4(i), §20.4 and Ch.20

►

20.4.5 $${\theta }_4(0,q)=\prod _{n=1}^{\mathrm{\infty }}\left(1-q^{2n}\right){\left(1-q^{2n-1}\right)}^2.$$

ⓘ

Symbols:

${\theta }_j(z,q)$: theta function, $n$: integer and $q$: nome

Referenced by:

(20.10.1)

Permalink:

http://dlmf.nist.gov/20.4.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §20.4(i), §20.4 and Ch.20

… ►

20.4.6 $${\theta }_1^{\prime }(0,q)={\theta }_2(0,q){\theta }_3(0,q){\theta }_4(0,q).$$

ⓘ

Symbols:

${\theta }_j(z,q)$: theta function and $q$: nome

A&S Ref:

16.28.6

Referenced by:

§20.9(i)

Permalink:

http://dlmf.nist.gov/20.4.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §20.4(i), §20.4(i), §20.4 and Ch.20

…

6: 20.8 Watson’s Expansions

… ►

20.8.1 $$\frac{{\theta }_2(0,q){\theta }_3(z,q){\theta }_4(z,q)}{{\theta }_2(z,q)}=2\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{{(-1)}^n{q}^{n^2}{\mathrm{e}}^{\mathrm{i}2nz}}{q^{-n}{\mathrm{e}}^{-\mathrm{i}z}+q^n{\mathrm{e}}^{\mathrm{i}z}}.$$

ⓘ

Symbols:

${\theta }_j(z,q)$: theta function, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $n$: integer, $z$: complex and $q$: nome

Permalink:

http://dlmf.nist.gov/20.8.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §20.8 and Ch.20

…

7: 22.11 Fourier and Hyperbolic Series

… ►

22.11.1 $$\mathrm{sn}(z,k)=\frac{2\pi }{Kk}\sum _{n=0}^{\mathrm{\infty }}\frac{q^{n+\frac{1}{2}}\sin \left((2n+1)\zeta \right)}{1-q^{2n+1}},$$

ⓘ

Symbols:

$\mathrm{sn}(z,k)$: Jacobian elliptic function, $\pi$: the ratio of the circumference of a circle to its diameter, $K\left(k\right)$: Legendre’s complete elliptic integral of the first kind, $q$: nome, $\sin z$: sine function, $z$: complex, $k$: modulus and $\zeta$: change of variable

A&S Ref:

16.23.1

Permalink:

http://dlmf.nist.gov/22.11.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §22.11 and Ch.22

►

22.11.2 $$\mathrm{cn}(z,k)=\frac{2\pi }{Kk}\sum _{n=0}^{\mathrm{\infty }}\frac{q^{n+\frac{1}{2}}\cos \left((2n+1)\zeta \right)}{1+q^{2n+1}},$$

ⓘ

Symbols:

$\mathrm{cn}(z,k)$: Jacobian elliptic function, $\pi$: the ratio of the circumference of a circle to its diameter, $K\left(k\right)$: Legendre’s complete elliptic integral of the first kind, $\cos z$: cosine function, $q$: nome, $z$: complex, $k$: modulus and $\zeta$: change of variable

A&S Ref:

16.23.2

Permalink:

http://dlmf.nist.gov/22.11.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §22.11 and Ch.22

►

22.11.3 $$\mathrm{dn}(z,k)=\frac{\pi }{2K}+\frac{2\pi }{K}\sum _{n=1}^{\mathrm{\infty }}\frac{q^n\cos \left(2n\zeta \right)}{1+q^{2n}}.$$

ⓘ

Symbols:

$\mathrm{dn}(z,k)$: Jacobian elliptic function, $\pi$: the ratio of the circumference of a circle to its diameter, $K\left(k\right)$: Legendre’s complete elliptic integral of the first kind, $\cos z$: cosine function, $q$: nome, $z$: complex, $k$: modulus and $\zeta$: change of variable

A&S Ref:

16.23.3

Permalink:

http://dlmf.nist.gov/22.11.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §22.11 and Ch.22

►

22.11.4 $$\mathrm{cd}(z,k)=\frac{2\pi }{Kk}\sum _{n=0}^{\mathrm{\infty }}\frac{{(-1)}^n{q}^{n+\frac{1}{2}}\cos \left((2n+1)\zeta \right)}{1-q^{2n+1}},$$

ⓘ

Symbols:

$\mathrm{cd}(z,k)$: Jacobian elliptic function, $\pi$: the ratio of the circumference of a circle to its diameter, $K\left(k\right)$: Legendre’s complete elliptic integral of the first kind, $\cos z$: cosine function, $q$: nome, $z$: complex, $k$: modulus and $\zeta$: change of variable

A&S Ref:

16.23.4

Permalink:

http://dlmf.nist.gov/22.11.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §22.11 and Ch.22

… ►

22.11.13 $${\mathrm{sn}}^2(z,k)=\frac{1}{k^2}\left(1-\frac{E}{K}\right)-\frac{2{\pi }^2}{k^2{K}^2}\sum _{n=1}^{\mathrm{\infty }}\frac{n{q}^n}{1-q^{2n}}\cos \left(2n\zeta \right).$$

ⓘ

Symbols:

$\mathrm{sn}(z,k)$: Jacobian elliptic function, $\pi$: the ratio of the circumference of a circle to its diameter, $K\left(k\right)$: Legendre’s complete elliptic integral of the first kind, $E\left(k\right)$: Legendre’s complete elliptic integral of the second kind, $\cos z$: cosine function, $q$: nome, $z$: complex, $k$: modulus and $\zeta$: change of variable

Referenced by:

§22.11

Permalink:

http://dlmf.nist.gov/22.11.E13

Encodings:

pMML, png, TeX

See also:

Annotations for §22.11 and Ch.22

…

8: 20.7 Identities

… ►

20.7.1 $${\theta }_3^2(0,q){\theta }_3^2(z,q)={\theta }_4^2(0,q){\theta }_4^2(z,q)+{\theta }_2^2(0,q){\theta }_2^2(z,q),$$

ⓘ

Symbols:

${\theta }_j(z,q)$: theta function, $z$: complex and $q$: nome

A&S Ref:

16.28.3

Permalink:

http://dlmf.nist.gov/20.7.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §20.7(i), §20.7 and Ch.20

►

20.7.2 $${\theta }_3^2(0,q){\theta }_4^2(z,q)={\theta }_2^2(0,q){\theta }_1^2(z,q)+{\theta }_4^2(0,q){\theta }_3^2(z,q),$$

ⓘ

Symbols:

${\theta }_j(z,q)$: theta function, $z$: complex and $q$: nome

A&S Ref:

16.28.2

Permalink:

http://dlmf.nist.gov/20.7.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §20.7(i), §20.7 and Ch.20

►

20.7.3 $${\theta }_2^2(0,q){\theta }_4^2(z,q)={\theta }_3^2(0,q){\theta }_1^2(z,q)+{\theta }_4^2(0,q){\theta }_2^2(z,q),$$

ⓘ

Symbols:

${\theta }_j(z,q)$: theta function, $z$: complex and $q$: nome

A&S Ref:

16.28.1

Permalink:

http://dlmf.nist.gov/20.7.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §20.7(i), §20.7 and Ch.20

►

20.7.4 $${\theta }_2^2(0,q){\theta }_3^2(z,q)={\theta }_4^2(0,q){\theta }_1^2(z,q)+{\theta }_3^2(0,q){\theta }_2^2(z,q).$$

ⓘ

Symbols:

${\theta }_j(z,q)$: theta function, $z$: complex and $q$: nome

A&S Ref:

16.28.4

Permalink:

http://dlmf.nist.gov/20.7.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §20.7(i), §20.7 and Ch.20

… ►

20.7.5 $${\theta }_3^4(0,q)={\theta }_2^4(0,q)+{\theta }_4^4(0,q).$$

ⓘ

Symbols:

${\theta }_j(z,q)$: theta function and $q$: nome

A&S Ref:

16.28.5

Referenced by:

§23.6(ii)

Permalink:

http://dlmf.nist.gov/20.7.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §20.7(i), §20.7 and Ch.20

…

9: 20.3 Graphics

… ►

§20.3(i) $\theta$-Functions: Real Variable and Real Nome

… ►

►►

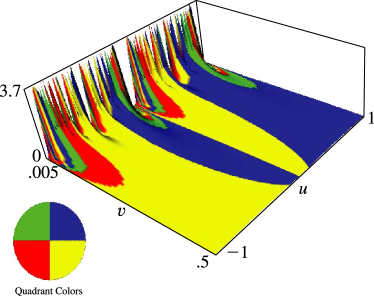
Figure 20.3.2: ${\theta }_1(\pi x,q)$, $0\le x\le 2$, $q$ = 0. … Magnify

►

►►

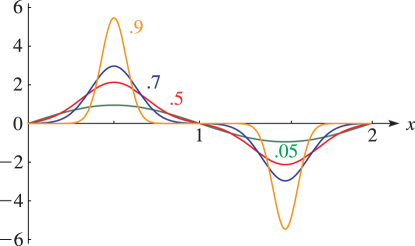
Figure 20.3.3: ${\theta }_2(\pi x,q)$, $0\le x\le 2$, $q$ = 0. … Magnify

… ►

§20.3(ii) $\theta$-Functions: Complex Variable and Real Nome

… ►

►

►

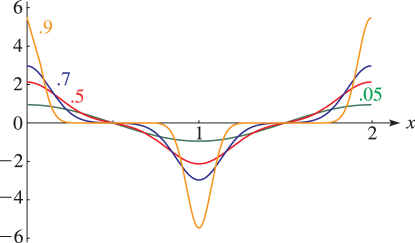
Figure 20.3.18: ${\theta }_1\left(0.1\right|u+\mathrm{i}v)$, $-1\le u\le 1$, $0.005\le v\le 0.5$. …1 of $z$ is chosen arbitrarily since ${\theta }_1$ vanishes identically when $z=0$. Magnify 3D Help

…

10: 20.11 Generalizations and Analogs

… ►

20.11.6 $${\phi }_{m,1}(z,q)=\frac{{\theta }_1^{\prime }(0,q){\theta }_m(z,q)}{{\theta }_m(0,q){\theta }_1(z,q)},$$ $m=2,3,4$,

ⓘ

Symbols:

${\theta }_j(z,q)$: theta function, ${\phi }_{n,m}(z,q)$: combined theta function, $m$: integer, $z$: complex and $q$: nome

Permalink:

http://dlmf.nist.gov/20.11.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §20.11(v), §20.11 and Ch.20

►

20.11.7 $${\phi }_{1,n}(z,q)=\frac{{\theta }_n(0,q){\theta }_1(z,q)}{{\theta }_1^{\prime }(0,q){\theta }_n(z,q)},$$ $n=2,3,4$,

ⓘ

Symbols:

${\theta }_j(z,q)$: theta function, ${\phi }_{n,m}(z,q)$: combined theta function, $n$: integer, $z$: complex and $q$: nome

Permalink:

http://dlmf.nist.gov/20.11.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §20.11(v), §20.11 and Ch.20

►

20.11.8 $${\phi }_{m,n}(z,q)=\frac{{\theta }_n(0,q){\theta }_m(z,q)}{{\theta }_m(0,q){\theta }_n(z,q)},$$ $m,n=2,3,4$.

ⓘ

Symbols:

${\theta }_j(z,q)$: theta function, ${\phi }_{n,m}(z,q)$: combined theta function, $m$: integer, $n$: integer, $z$: complex and $q$: nome

Permalink:

http://dlmf.nist.gov/20.11.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §20.11(v), §20.11 and Ch.20

… ►

20.11.9 $${\phi }_{m,n}(z,q)={\phi }_{m,1}(z,q){\phi }_{1,n}(z,q)=\frac{1}{{\phi }_{n,m}(z,q)}=\frac{{\phi }_{m,1}(z,q)}{{\phi }_{n,1}(z,q)}=\frac{{\phi }_{1,n}(z,q)}{{\phi }_{1,m}(z,q)}.$$

ⓘ

Symbols:

${\phi }_{n,m}(z,q)$: combined theta function, $m$: integer, $n$: integer, $z$: complex and $q$: nome

Permalink:

http://dlmf.nist.gov/20.11.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §20.11(v), §20.11 and Ch.20

…