About the Project

Next 10 matching pages

Jacobi identities

♦ 1—10 of 26 matching pages ♦

(0.002 seconds)

1—10 of 26 matching pages

1: 20.4 Values at $z$ = 0

… ►

Jacobi’s Identity

…

2: 27.13 Functions

… ►

27.13.5

(\vartheta\left(x\right))^{2}=1+\sum_{n=1}^{\infty}r_{2}\left(n\right)x^{n}.

ⓘ

Symbols:: $\vartheta\left(\NVar{x}\right)=\theta_{3}\left(0,x\right)$ : alternative notation, $r_{\NVar{k}}\left(\NVar{n}\right)$ : number of squares, $n$ : positive integer and $x$ : real number
Referenced by:: §27.13(iv)
Permalink:: http://dlmf.nist.gov/27.13.E5
Encodings:: pMML, png, TeX
See also:: Annotations for §27.13(iv), §27.13 and Ch.27

►One of Jacobi’s identities implies that … ►Also, Milne (1996, 2002) announce new infinite families of explicit formulas extending Jacobi’s identities. …

3: Bibliography K

… ►

A. Khare, A. Lakshminarayan, and U. Sukhatme (2003) Cyclic identities for Jacobi elliptic and related functions. J. Math. Phys. 44 (4), pp. 1822–1841.

ⓘ

External Links:: ISSN 0022-2488, Document, MathReview (Zhi Guo Liu), ZentralBlatt
Referenced by:: §22.9(iv), §22.9(v).
Encodings:: BibTeX

►

A. Khare and U. Sukhatme (2002) Cyclic identities involving Jacobi elliptic functions. J. Math. Phys. 43 (7), pp. 3798–3806.

ⓘ

External Links:: ISSN 0022-2488, Document, MathReview, ZentralBlatt
Referenced by:: §22.9(i), §22.9(ii), §22.9(iii), §22.9(iv), §22.9(v).
Encodings:: BibTeX

…

4: Bibliography B

… ►

J. M. Borwein and P. B. Borwein (1991) A cubic counterpart of Jacobi’s identity and the AGM. Trans. Amer. Math. Soc. 323 (2), pp. 691–701.

ⓘ

External Links:: ISSN 0002-9947, FullText, MathReview (Bruce C. Berndt), ZentralBlatt
Referenced by:: §15.8(v).
Encodings:: BibTeX

…

5: 20.3 Graphics

… ►

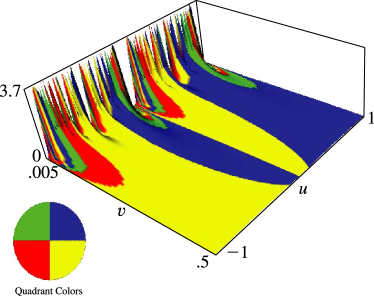
See accompanying text — Figure 20.3.18: $\theta_{1}\left(0.1\middle|u+iv\right)$ , $-1\leq u\leq 1$ , $0.005\leq v\leq 0.5$ . …1 of $z$ is chosen arbitrarily since $\theta_{1}$ vanishes identically when $z=0$ . Magnify 3D Help

…

6: 20.7 Identities

… ►

20.7.15

A\equiv A(\tau)=\ifrac{1}{\theta_{4}\left(0\middle|2\tau\right)},

ⓘ

Defines:: $A$ (locally)
Symbols:: $\theta_{\NVar{j}}\left(\NVar{z}\middle|\NVar{\tau}\right)$ : theta function, $\equiv$ : equals by definition and $\tau$ : lattice parameter
Permalink:: http://dlmf.nist.gov/20.7.E15
Encodings:: pMML, png, TeX
See also:: Annotations for §20.7(vi), §20.7 and Ch.20

… ►

20.7.20

B\equiv B(\tau)=\ifrac{1}{\left(\theta_{3}\left(0\middle|\tau\right)\theta_{4}% \left(0\middle|\tau\right)\theta_{3}\left(\tfrac{1}{4}\pi\middle|\tau\right)% \right)},

ⓘ

Defines:: $B$ (locally)
Symbols:: $\theta_{\NVar{j}}\left(\NVar{z}\middle|\NVar{\tau}\right)$ : theta function, $\pi$ : the ratio of the circumference of a circle to its diameter, $\equiv$ : equals by definition and $\tau$ : lattice parameter
Permalink:: http://dlmf.nist.gov/20.7.E20
Encodings:: pMML, png, TeX
See also:: Annotations for §20.7(vi), §20.7 and Ch.20

…

7: 20.11 Generalizations and Analogs

… ►This is the discrete analog of the Poisson identity (§1.8(iv)). … ►This is Jacobi’s inversion problem of §20.9(ii). … ►Each provides an extension of Jacobi’s inversion problem. …

8: 22.8 Addition Theorems

… ►

22.8.14

\operatorname{sn}(u+v)=\frac{\operatorname{sn}u\operatorname{cn}u\operatorname% {dn}v+\operatorname{sn}v\operatorname{cn}v\operatorname{dn}u}{\operatorname{cn% }u\operatorname{cn}v+\operatorname{sn}u\operatorname{dn}u\operatorname{sn}v% \operatorname{dn}v},

ⓘ

Symbols:: $\operatorname{cn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $\operatorname{dn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $\operatorname{sn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $u$ : complex, $v$ : complex and $k$ : modulus
Permalink:: http://dlmf.nist.gov/22.8.E14
Encodings:: pMML, png, TeX
See also:: Annotations for §22.8(ii), §22.8 and Ch.22

►

22.8.15

\operatorname{cn}(u+v)=\frac{\operatorname{sn}u\operatorname{cn}u\operatorname% {dn}v-\operatorname{sn}v\operatorname{cn}v\operatorname{dn}u}{\operatorname{sn% }u\operatorname{cn}v\operatorname{dn}v-\operatorname{sn}v\operatorname{cn}u% \operatorname{dn}u},

ⓘ

Symbols:: $\operatorname{cn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $\operatorname{dn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $\operatorname{sn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $u$ : complex, $v$ : complex and $k$ : modulus
Permalink:: http://dlmf.nist.gov/22.8.E15
Encodings:: pMML, png, TeX
See also:: Annotations for §22.8(ii), §22.8 and Ch.22

… ►

22.8.17

\operatorname{dn}(u+v)=\frac{\operatorname{sn}u\operatorname{cn}v\operatorname% {dn}u-\operatorname{sn}v\operatorname{cn}u\operatorname{dn}v}{\operatorname{sn% }u\operatorname{cn}v\operatorname{dn}v-\operatorname{sn}v\operatorname{cn}u% \operatorname{dn}u},

ⓘ

Symbols:: $\operatorname{cn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $\operatorname{dn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $\operatorname{sn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $u$ : complex, $v$ : complex and $k$ : modulus
Permalink:: http://dlmf.nist.gov/22.8.E17
Encodings:: pMML, png, TeX
See also:: Annotations for §22.8(ii), §22.8 and Ch.22

… ►

22.8.23

\begin{vmatrix}\operatorname{sn}z_{1}\operatorname{cn}z_{1}&\operatorname{cn}z% _{1}\operatorname{dn}z_{1}&\operatorname{cn}z_{1}&\operatorname{dn}z_{1}\\ \operatorname{sn}z_{2}\operatorname{cn}z_{2}&\operatorname{cn}z_{2}% \operatorname{dn}z_{2}&\operatorname{cn}z_{2}&\operatorname{dn}z_{2}\\ \operatorname{sn}z_{3}\operatorname{cn}z_{3}&\operatorname{cn}z_{3}% \operatorname{dn}z_{3}&\operatorname{cn}z_{3}&\operatorname{dn}z_{3}\\ \operatorname{sn}z_{4}\operatorname{cn}z_{4}&\operatorname{cn}z_{4}% \operatorname{dn}z_{4}&\operatorname{cn}z_{4}&\operatorname{dn}z_{4}\end{% vmatrix}=0.

ⓘ

Symbols:: $\operatorname{cn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $\operatorname{dn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $\operatorname{sn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $\det$ : determinant, $z$ : complex and $k$ : modulus
Permalink:: http://dlmf.nist.gov/22.8.E23
Encodings:: pMML, png, TeX
See also:: Annotations for §22.8(iii), §22.8 and Ch.22

►For these and related identities see Copson (1935, pp. 415–416). …

9: 22.17 Moduli Outside the Interval [0,1]

… ►

22.17.1

\operatorname{pq}\left(z,k\right)=\operatorname{pq}\left(z,-k\right),

ⓘ

Symbols:: $\operatorname{pq}\left(\NVar{z},\NVar{k}\right)$ : generic Jacobian elliptic function, $z$ : complex and $k$ : modulus
Permalink:: http://dlmf.nist.gov/22.17.E1
Encodings:: pMML, png, TeX
See also:: Annotations for §22.17(i), §22.17 and Ch.22

… ►

22.17.2

\operatorname{sn}\left(z,1/k\right)=k\operatorname{sn}\left(z/k,k\right),

ⓘ

Symbols:: $\operatorname{sn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $z$ : complex and $k$ : modulus
A&S Ref:: 16.11.2
Permalink:: http://dlmf.nist.gov/22.17.E2
Encodings:: pMML, png, TeX
See also:: Annotations for §22.17(i), §22.17 and Ch.22

►

22.17.3

\operatorname{cn}\left(z,1/k\right)=\operatorname{dn}\left(z/k,k\right),

ⓘ

Symbols:: $\operatorname{cn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $\operatorname{dn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $z$ : complex and $k$ : modulus
A&S Ref:: 16.11.3
Permalink:: http://dlmf.nist.gov/22.17.E3
Encodings:: pMML, png, TeX
See also:: Annotations for §22.17(i), §22.17 and Ch.22

►

22.17.4

\operatorname{dn}\left(z,1/k\right)=\operatorname{cn}\left(z/k,k\right).

ⓘ

Symbols:: $\operatorname{cn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $\operatorname{dn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $z$ : complex and $k$ : modulus
A&S Ref:: 16.11.4
Permalink:: http://dlmf.nist.gov/22.17.E4
Encodings:: pMML, png, TeX
See also:: Annotations for §22.17(i), §22.17 and Ch.22

… ►In terms of the coefficients of the power series of §22.10(i), the above equations are polynomial identities in

k

. …

10: 22.9 Cyclic Identities

§22.9 Cyclic Identities

… ►

§22.9(ii) Typical Identities of Rank 2

… ► ►

§22.9(iii) Typical Identities of Rank 3

… ►

Next 10 matching pages

© 2010–2024 NIST / Disclaimer / Feedback.

NIST

Site Privacy Accessibility Privacy Program Copyrights Vulnerability Disclosure No Fear Act Policy FOIA Environmental Policy Scientific Integrity Information Quality Standards Commerce.gov Science.gov USA.gov