Hankel

SearchAdvancedHelp

(0.001 seconds)

11—20 of 73 matching pages

11: 10.3 Graphics

… ►

§10.3(ii) Real Order, Complex Variable

… ►

►

►

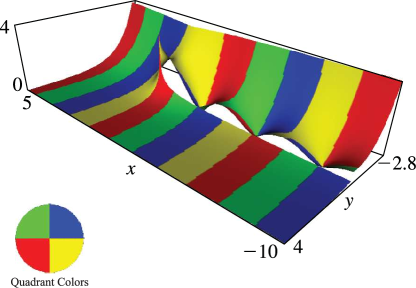
Figure 10.3.10: $H_0^{(1)}\left(x+\mathrm{i}y\right)$, $-10\le x\le 5$, $-2.8\le y\le 4$. … Magnify 3D Help

… ►

►

►

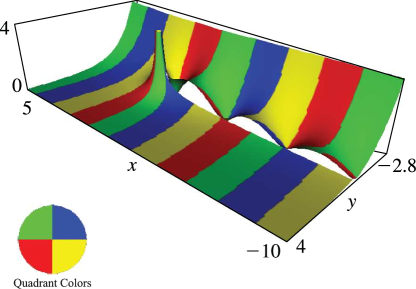
Figure 10.3.12: $H_1^{(1)}\left(x+\mathrm{i}y\right)$, $-10\le x\le 5$, $-2.8\le y\le 4$. … Magnify 3D Help

… ►

►

►

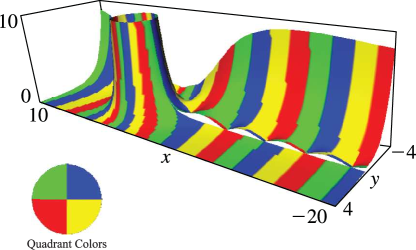
Figure 10.3.14: $H_5^{(1)}\left(x+\mathrm{i}y\right)$, $-20\le x\le 10$, $-4\le y\le 4$. … Magnify 3D Help

… ►

►

►

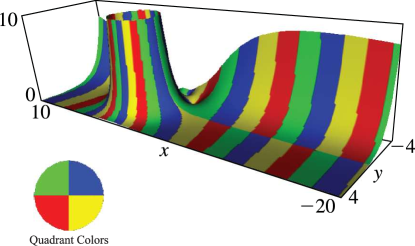
Figure 10.3.16: $H_{5.5}^{(1)}\left(x+\mathrm{i}y\right)$, $-20\le x\le 10$, $-4\le y\le 4$. … Magnify 3D Help

…

12: 10.8 Power Series

§10.8 Power Series

… ►When $\nu$ is not an integer the corresponding expansions for $Y_{\nu }\left(z\right)$, $H_{\nu }^{(1)}\left(z\right)$, and $H_{\nu }^{(2)}\left(z\right)$ are obtained by combining (10.2.2) with (10.2.3), (10.4.7), and (10.4.8). … ►The corresponding results for $H_n^{(1)}\left(z\right)$ and $H_n^{(2)}\left(z\right)$ are obtained via (10.4.3) with $\nu =n$. …

13: 11.1 Special Notation

… ►For the functions $J_{\nu }\left(z\right)$, $Y_{\nu }\left(z\right)$, $H_{\nu }^{(1)}\left(z\right)$, $H_{\nu }^{(2)}\left(z\right)$, $I_{\nu }\left(z\right)$, and $K_{\nu }\left(z\right)$ see §§10.2(ii), 10.25(ii). …

14: 10.17 Asymptotic Expansions for Large Argument

… ►

§10.17(i) Hankel’s Expansions

… ► … ►

§10.17(iii) Error Bounds for Real Argument and Order

… ►

§10.17(v) Exponentially-Improved Expansions

… ►For higher re-expansions of the remainder terms see Olde Daalhuis and Olver (1995a) and Olde Daalhuis (1995, 1996).

15: 10.76 Approximations

… ►

§10.76(ii) Bessel Functions, Hankel Functions, and Modified Bessel Functions

…

16: 10.74 Methods of Computation

… ►For evaluation of the Hankel functions $H_{\nu }^{(1)}\left(z\right)$ and $H_{\nu }^{(2)}\left(z\right)$ for complex values of $\nu$ and $z$ based on the integral representations (10.9.18) see Remenets (1973). … ► ►

§10.74(vi) Zeros and Associated Values

… ►

Hankel Transform

… ►The spherical Bessel transform is the Hankel transform (10.22.76) in the case when $\nu$ is half an odd positive integer. …

17: 10.19 Asymptotic Expansions for Large Order

§10.19 Asymptotic Expansions for Large Order

►

§10.19(i) Asymptotic Forms

… ►

10.19.2 $$Y_{\nu }\left(z\right)\sim -\mathrm{i}{H}_{\nu }^{(1)}\left(z\right)\sim \mathrm{i}{H}_{\nu }^{(2)}\left(z\right)\sim -\sqrt{\frac{2}{\pi \nu }}{\left(\frac{\mathrm{e}z}{2\nu }\right)}^{-\nu }.$$

ⓘ

Symbols:

$Y_{\nu }\left(z\right)$: Bessel function of the second kind, $H_{\nu }^{(1)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $H_{\nu }^{(2)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $z$: complex variable and $\nu$: complex parameter

A&S Ref:

9.3.1

Referenced by:

§10.41(i)

Permalink:

http://dlmf.nist.gov/10.19.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §10.19(i), §10.19 and Ch.10

… ►

§10.19(iii) Transition Region

… ►See also §10.20(i).

18: 10.27 Connection Formulas

… ►

10.27.7 $$I_{\nu }\left(z\right)=\frac{1}{2}{\mathrm{e}}^{\mp \nu \pi \mathrm{i}/2}\left(H_{\nu }^{(1)}\left(z{\mathrm{e}}^{\pm \pi \mathrm{i}/2}\right)+H_{\nu }^{(2)}\left(z{\mathrm{e}}^{\pm \pi \mathrm{i}/2}\right)\right),$$ $-\pi \le \pm \mathrm{ph}z\le \frac{1}{2}\pi$.

ⓘ

Symbols:

$H_{\nu }^{(1)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $H_{\nu }^{(2)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $I_{\nu }\left(z\right)$: modified Bessel function of the first kind, $\mathrm{ph}$: phase, $z$: complex variable and $\nu$: complex parameter

Permalink:

http://dlmf.nist.gov/10.27.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §10.27 and Ch.10

►

10.27.8

ⓘ

Symbols:

$H_{\nu }^{(1)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $H_{\nu }^{(2)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $K_{\nu }\left(z\right)$: modified Bessel function of the second kind, $\mathrm{ph}$: phase, $z$: complex variable and $\nu$: complex parameter

A&S Ref:

9.6.4

Referenced by:

§10.16, §10.26(ii), §10.27, §10.27, §10.32(ii), §10.39, §10.40(ii), §10.40(iii), §10.41(i), §10.42, §10.43(ii), §10.44(i), §10.44(ii), §10.44(iii), §10.47(iv), (9.7.16), §9.7(iii)

Permalink:

http://dlmf.nist.gov/10.27.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §10.27 and Ch.10

…

19: 10.50 Wronskians and Cross-Products

… ►

$$𝒲\left\{{𝗁}_n^{(1)}\left(z\right),{𝗁}_n^{(2)}\left(z\right)\right\}=-2\mathrm{i}{z}^{-2}.$$

…

20: 10.54 Integral Representations

… ►

${𝗁}_n^{(1)}\left(z\right)={\displaystyle \frac{{(-\mathrm{i})}^{n+1}}{\pi }}{\displaystyle {\int }_{\mathrm{i}\mathrm{\infty }}^{(1+)}}{\mathrm{e}}^{\mathrm{i}zt}{Q}_n\left(t\right)dt,$

►

${𝗁}_n^{(2)}\left(z\right)={\displaystyle \frac{{(-\mathrm{i})}^{n+1}}{\pi }}{\displaystyle {\int }_{\mathrm{i}\mathrm{\infty }}^{(-1+)}}{\mathrm{e}}^{\mathrm{i}zt}{Q}_n\left(t\right)dt,$

…