Hahn class orthogonal polynomials

SearchAdvancedHelp

(0.009 seconds)

1—10 of 16 matching pages

1: 18.24 Hahn Class: Asymptotic Approximations

§18.24 Hahn Class: Asymptotic Approximations

… ►Similar approximations are included for Jacobi, Krawtchouk, and Meixner polynomials.

2: 18.19 Hahn Class: Definitions

§18.19 Hahn Class: Definitions

… ►

Hahn, Krawtchouk, Meixner, and Charlier

… ►

Table 18.19.1: Orthogonality properties for Hahn, Krawtchouk, Meixner, and Charlier OP’s: discrete sets, weight functions, standardizations, and parameter constraints.

► ►►

	$p_n(x)$	$X$	$w_x$	$h_n$
…

►

►

Table 18.19.2: Hahn, Krawtchouk, Meixner, and Charlier OP’s: leading coefficients.

► ►►

$p_n(x)$	$k_n$
…

►

… ►A special case of (18.19.8) is $w^{(1/2)}(x;\pi /2)=\frac{\pi }{\cosh \left(\pi x\right)}$.

3: 18.20 Hahn Class: Explicit Representations

… ►

§18.20(i) Rodrigues Formulas

… ►

§18.20(ii) Hypergeometric Function and Generalized Hypergeometric Functions

…

4: 18.1 Notation

… ►

$${(z_1,\mathrm{\dots },z_k;q)}_{\mathrm{\infty }}={(z_1;q)}_{\mathrm{\infty }}\mathrm{\cdots }{(z_k;q)}_{\mathrm{\infty }}.$$

… ►

Hahn Class OP’s

…

5: 18.21 Hahn Class: Interrelations

§18.21 Hahn Class: Interrelations

►

§18.21(i) Dualities

… ►

§18.21(ii) Limit Relations and Special Cases

… ►

►►

Figure 18.21.1: Askey scheme. … Magnify

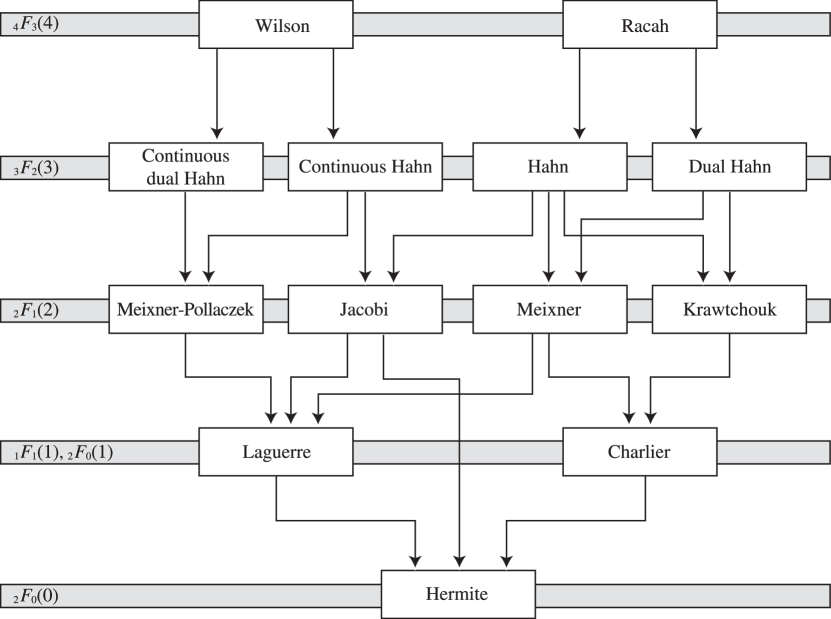6: 18.27 $q$-Hahn Class

§18.27 $q$-Hahn Class

… ►

§18.27(ii) $q$-Hahn Polynomials

… ►

§18.27(iii) Big $q$-Jacobi Polynomials

… ►

§18.27(iv) Little $q$-Jacobi Polynomials

… ►

Limit Relations

…

7: 18.29 Asymptotic Approximations for $q$-Hahn and Askey–Wilson Classes

§18.29 Asymptotic Approximations for $q$-Hahn and Askey–Wilson Classes

…

8: 18.23 Hahn Class: Generating Functions

§18.23 Hahn Class: Generating Functions

… ►

Hahn

…

9: 18.22 Hahn Class: Recurrence Relations and Differences

… ►

§18.22(i) Recurrence Relations in $n$

… ►

§18.22(ii) Difference Equations in $x$

… ►

§18.22(iii) $x$-Differences

…

10: 18.38 Mathematical Applications

… ► …