Gegenbauer addition theorem

SearchAdvancedHelp

(0.002 seconds)

8 matching pages

1: 10.44 Sums

… ►

Graf’s and Gegenbauer’s Addition Theorems

…

2: 10.23 Sums

… ►

Graf’s and Gegenbauer’s Addition Theorems

… ►

►►

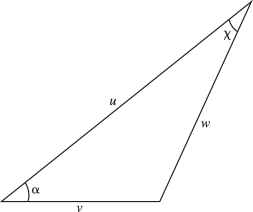
Figure 10.23.1: Graf’s and Gegenbauer’s addition theorems. Magnify

…

3: Bibliography C

… ►

New proof of the addition theorem for Gegenbauer polynomials. SIAM J. Math. Anal. 2, pp. 347–351.

ⓘ

External Links:

ISSN 1095-7154, Document, MathReview (Mary L. Boas), ZentralBlatt

Referenced by:

§18.18(ii).

Encodings:

BibTeX

… ►

Fourier, Gegenbauer and Jacobi expansions for a power-law fundamental solution of the polyharmonic equation and polyspherical addition theorems. SIGMA Symmetry Integrability Geom. Methods Appl. 9, pp. Paper 042, 26.

ⓘ

External Links:

ISSN 1815-0659, Document, MathReview (Heinrich Begehr), ZentralBlatt

Referenced by:

§14.28(ii), §14.28(ii).

Encodings:

BibTeX

…

4: 18.18 Sums

… ►

§18.18(ii) Addition Theorems

►

Ultraspherical

… ►

Legendre

… ►

Laguerre

… ►

Hermite

…

5: 10.60 Sums

… ►

§10.60(i) Addition Theorems

…

6: 14.28 Sums

… ►

§14.28(i) Addition Theorem

… ►For generalizations in terms of Gegenbauer and Jacobi polynomials, see Theorem 2. 1 in Cohl (2013b) and Theorem 1 in Cohl (2013a) respectively. …

7: 18.17 Integrals

… ►

18.17.5 $$\frac{C_n^{(\lambda )}\left(\cos {\theta }_1\right)}{C_n^{(\lambda )}\left(1\right)}\frac{C_n^{(\lambda )}\left(\cos {\theta }_2\right)}{C_n^{(\lambda )}\left(1\right)}=\frac{\mathrm{\Gamma }\left(\lambda +\frac{1}{2}\right)}{{\pi }^{\frac{1}{2}}\mathrm{\Gamma }\left(\lambda \right)}{\int }_0^{\pi }\frac{C_n^{(\lambda )}\left(\cos {\theta }_1\cos {\theta }_2+\sin {\theta }_1\sin {\theta }_2\cos \varphi \right)}{C_n^{(\lambda )}\left(1\right)}{(\sin \varphi )}^{2\lambda -1}d\varphi ,$$ $\lambda >0$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $dx$: differential of $x$ , $\int$: integral, $\sin z$: sine function, $C_n^{(\lambda )}\left(x\right)$: ultraspherical (or Gegenbauer) polynomial and $n$: nonnegative integer

Referenced by:

§18.17(ii), §18.17(ii), §18.18(ii)

Permalink:

http://dlmf.nist.gov/18.17.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §18.17(ii), §18.17(ii), §18.17 and Ch.18

… ►For addition formulas corresponding to (18.17.5) and (18.17.6) see (18.18.8) and (18.18.9), respectively. … ►

18.17.12 $$\frac{\mathrm{\Gamma }\left(\lambda -\mu \right)C_n^{(\lambda -\mu )}\left(x^{-\frac{1}{2}}\right)}{x^{\lambda -\mu +\frac{1}{2}n}}={\int }_x^{\mathrm{\infty }}\frac{\mathrm{\Gamma }\left(\lambda \right)C_n^{(\lambda )}\left(y^{-\frac{1}{2}}\right)}{y^{\lambda +\frac{1}{2}n}}\frac{{(y-x)}^{\mu -1}}{\mathrm{\Gamma }\left(\mu \right)}dy,$$ $\lambda >\mu >0$, $x>0$,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $dx$: differential of $x$ , $\int$: integral, $C_n^{(\lambda )}\left(x\right)$: ultraspherical (or Gegenbauer) polynomial, $y$: real variable, $n$: nonnegative integer and $x$: real variable

Referenced by:

§18.17(iv)

Permalink:

http://dlmf.nist.gov/18.17.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §18.17(iv), §18.17(iv), §18.17 and Ch.18

►

18.17.13 $$\frac{x^{\frac{1}{2}n}{(x-1)}^{\lambda +\mu -\frac{1}{2}}}{\mathrm{\Gamma }\left(\lambda +\mu +\frac{1}{2}\right)}\frac{C_n^{(\lambda +\mu )}\left(x^{-\frac{1}{2}}\right)}{C_n^{(\lambda +\mu )}\left(1\right)}={\int }_1^x\frac{y^{\frac{1}{2}n}{(y-1)}^{\lambda -\frac{1}{2}}}{\mathrm{\Gamma }\left(\lambda +\frac{1}{2}\right)}\frac{C_n^{(\lambda )}\left(y^{-\frac{1}{2}}\right)}{C_n^{(\lambda )}\left(1\right)}\frac{{(x-y)}^{\mu -1}}{\mathrm{\Gamma }\left(\mu \right)}dy,$$ $\mu >0$, $x>1$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $dx$: differential of $x$ , $\int$: integral, $C_n^{(\lambda )}\left(x\right)$: ultraspherical (or Gegenbauer) polynomial, $y$: real variable, $n$: nonnegative integer and $x$: real variable

Referenced by:

§1.15(vi), §18.17(iv)

Permalink:

http://dlmf.nist.gov/18.17.E13

Encodings:

pMML, png, TeX

See also:

Annotations for §18.17(iv), §18.17(iv), §18.17 and Ch.18

… ►

18.17.16_5 $${\int }_{-1}^1{(1-x^2)}^{\lambda -\frac{1}{2}}{C}_n^{(\lambda )}\left(x\right){\mathrm{e}}^{\mathrm{i}xy}dx=\frac{2\pi {\mathrm{i}}^n\mathrm{\Gamma }\left(n+2\lambda \right)J_{n+\lambda }\left(y\right)}{n!\mathrm{\Gamma }\left(\lambda \right){(2y)}^{\lambda }},$$

ⓘ

Symbols:

$J_{\nu }\left(z\right)$: Bessel function of the first kind, $\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $!$: factorial (as in $n!$), $\mathrm{i}$: imaginary unit, $\int$: integral, $C_n^{(\lambda )}\left(x\right)$: ultraspherical (or Gegenbauer) polynomial, $y$: real variable, $n$: nonnegative integer and $x$: real variable

Referenced by:

§18.17(v), Erratum (V1.2.0) Section 18.17

Permalink:

http://dlmf.nist.gov/18.17.E16_5

Encodings:

pMML, png, TeX

Addition (effective with 1.2.0):

This equation was added.

See also:

Annotations for §18.17(v), §18.17(v), §18.17 and Ch.18

…

8: Errata

… ►We now include Markov’s Theorem. … ►

Equation (5.2.9).

►

Equations (10.22.78), (10.22.79).

… ►

Equation (16.16.5_5).

… ►

Equation (4.13.5_3) (suggested by Warren Smith on 2023-08-10).

…