Ferrers functions
(0.005 seconds)
1—10 of 48 matching pages
1: 14.1 Special Notation
§14.1 Special Notation
… ►The main functions treated in this chapter are the Legendre functions , , , ; Ferrers functions , (also known as the Legendre functions on the cut); associated Legendre functions , , ; conical functions , , , , (also known as Mehler functions). …2: 14.32 Methods of Computation
§14.32 Methods of Computation
…3: 14.7 Integer Degree and Order
§14.7 Integer Degree and Order
… ►§14.7(ii) Rodrigues-Type Formulas
… ►§14.7(iii) Reflection Formulas
… ►§14.7(iv) Generating Functions
… ►4: 14.17 Integrals
…
►
§14.17(i) Indefinite Integrals
… ►§14.17(ii) Barnes’ Integral
… ►§14.17(iii) Orthogonality Properties
… ►§14.17(v) Laplace Transforms
… ►§14.17(vi) Mellin Transforms
…5: 14.5 Special Values
6: 14.10 Recurrence Relations and Derivatives
7: 14.4 Graphics
…
►
►
►
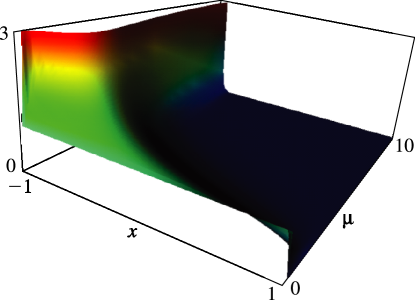
Figure 14.4.15:
, .
Magnify
3D
Help
►
►
►
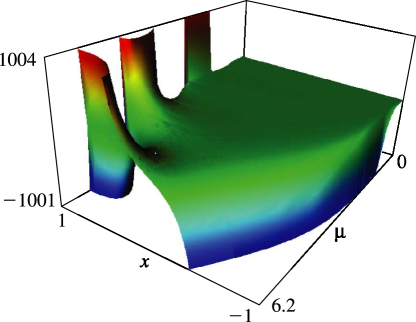
Figure 14.4.16:
, .
Magnify
3D
Help
…
§14.4(i) Ferrers Functions: 2D Graphs
… ►§14.4(ii) Ferrers Functions: 3D Surfaces
… ►8: 14.18 Sums
§14.18 Sums
… ►§14.18(ii) Addition Theorems
… ►
14.18.3
…
►The formulas are also valid with the Ferrers functions as in §14.3(i) with .
…
►
9: 14.9 Connection Formulas
…
►
§14.9(i) Connections Between , , ,
… ►
14.9.3
►
14.9.4
.
…
►
§14.9(ii) Connections Between , ,
… ►
14.9.9
…