Fejér kernel

SearchAdvancedHelp

(0.001 seconds)

1—10 of 34 matching pages

1: 1.15 Summability Methods

… ►

Poisson Kernel

… ►

Fejér Kernel

… ►

1.15.17 $$K_n(\theta )\to 0,$$

ⓘ

Symbols:

$n$: nonnegative integer and $K_n(\theta )$: Fejér kernel

Permalink:

http://dlmf.nist.gov/1.15.E17

Encodings:

pMML, png, TeX

See also:

Annotations for §1.15(iii), §1.15(iii), §1.15 and Ch.1

… ►

Poisson Kernel

… ►

Fejér Kernel

…

2: Bibliography W

… ►

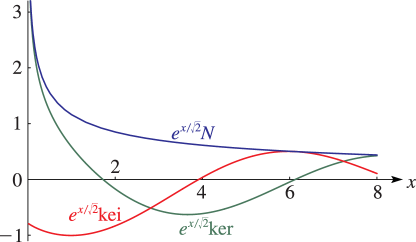
Fast construction of the Fejér and Clenshaw-Curtis quadrature rules. BIT 46 (1), pp. 195–202.

ⓘ

External Links:

ISSN 0006-3835, Document, MathReview Entry, ZentralBlatt

Referenced by:

§3.5(iv).

Encodings:

BibTeX

… ►

On a generalization of the functions $\mathrm{ber}$ x, $\mathrm{bei}$ x, $\ker$ x, $\mathrm{kei}$ x. Quart. J. Pure Appl. Math. 42, pp. 316–342.

ⓘ

External Links:

ZentralBlatt

Referenced by:

§10.61(iii), §10.61(iv), §10.65(i), §10.65(ii), §10.65(iii), §10.68(iii).

Encodings:

BibTeX

…

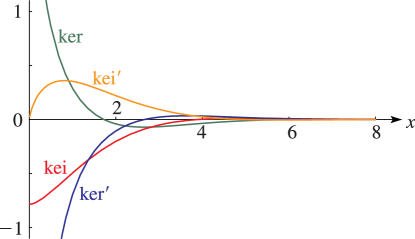
3: 10.62 Graphs

… ►

►►

Figure 10.62.2: $\ker x$, $\mathrm{kei}x$, ${\ker }^{\prime }x$, ${\mathrm{kei}}^{\prime }x$, $0\le x\le 8$. Magnify

… ►

►►

Figure 10.62.4: ${\mathrm{e}}^{x/\sqrt{2}}\ker x$, ${\mathrm{e}}^{x/\sqrt{2}}\mathrm{kei}x$, ${\mathrm{e}}^{x/\sqrt{2}}N\left(x\right)$, $0\le x\le 8$. Magnify

4: 10.61 Definitions and Basic Properties

… ►When $\nu =0$ suffices on $\mathrm{ber}$, $\mathrm{bei}$, $\ker$, and $\mathrm{kei}$ are usually suppressed. ►Most properties of ${\mathrm{ber}}_{\nu }x$, ${\mathrm{bei}}_{\nu }x$, ${\ker }_{\nu }x$, and ${\mathrm{kei}}_{\nu }x$ follow straightforwardly from the above definitions and results given in preceding sections of this chapter. … ►

$${\ker }_{-\nu }x=\cos \left(\nu \pi \right){\ker }_{\nu }x-\sin \left(\nu \pi \right){\mathrm{kei}}_{\nu }x,$$

►

$${\mathrm{kei}}_{-\nu }x=\sin \left(\nu \pi \right){\ker }_{\nu }x+\cos \left(\nu \pi \right){\mathrm{kei}}_{\nu }x.$$

… ►

$${\ker }_{-n}x={(-1)}^n{\ker }_{n}x,{\mathrm{kei}}_{-n}x={(-1)}^n{\mathrm{kei}}_{n}x.$$

…

5: 31.10 Integral Equations and Representations

… ►

Kernel Functions

… ►The kernel $𝒦$ must satisfy … ►

Kernel Functions

… ►The kernel $𝒦$ must satisfy … ►leads to the kernel equation …

6: 10.67 Asymptotic Expansions for Large Argument

… ►

§10.67(i) ${\mathrm{ber}}_{\nu }x,{\mathrm{bei}}_{\nu }x,{\ker }_{\nu }x,{\mathrm{kei}}_{\nu }x$, and Derivatives

… ►

10.67.1 $${\ker }_{\nu }x\sim {\mathrm{e}}^{-x/\sqrt{2}}{\left(\frac{\pi }{2x}\right)}^{\frac{1}{2}}\sum _{k=0}^{\mathrm{\infty }}\frac{a_k(\nu )}{x^k}\cos \left(\frac{x}{\sqrt{2}}+\left(\frac{\nu }{2}+\frac{k}{4}+\frac{1}{8}\right)\pi \right),$$

ⓘ

Symbols:

${\ker }_{\nu }\left(x\right)$: Kelvin function, $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\mathrm{e}$: base of natural logarithm, $k$: nonnegative integer, $x$: real variable, $\nu$: complex parameter and $a_k(\nu )$: polynomial coefficient

A&S Ref:

9.10.3, 9.10.5--9.10.7 (modified)

Referenced by:

§10.61(v), §10.67(ii), §10.68(iii)

Permalink:

http://dlmf.nist.gov/10.67.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §10.67(i), §10.67 and Ch.10

… ►The contributions of the terms in ${\ker }_{\nu }x$, ${\mathrm{kei}}_{\nu }x$, ${\ker }_{\nu }^{\prime }x$, and ${\mathrm{kei}}_{\nu }^{\prime }x$ on the right-hand sides of (10.67.3), (10.67.4), (10.67.7), and (10.67.8) are exponentially small compared with the other terms, and hence can be neglected in the sense of Poincaré asymptotic expansions (§2.1(iii)). … ►

10.67.14 $$\ker x{\mathrm{kei}}^{\prime }x-{\ker }^{\prime }x\mathrm{kei}x\sim -\frac{\pi }{2x}{\mathrm{e}}^{-x\sqrt{2}}\left(\frac{1}{\sqrt{2}}-\frac{1}{8}\frac{1}{x}+\frac{9}{64\sqrt{2}}\frac{1}{x^2}-\frac{39}{512}\frac{1}{x^3}+\frac{75}{8192\sqrt{2}}\frac{1}{x^4}+\mathrm{\cdots }\right),$$

ⓘ

Symbols:

${\mathrm{kei}}_{\nu }\left(x\right)$: Kelvin function, ${\ker }_{\nu }\left(x\right)$: Kelvin function, $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm and $x$: real variable

A&S Ref:

9.10.32

Permalink:

http://dlmf.nist.gov/10.67.E14

Encodings:

pMML, png, TeX

See also:

Annotations for §10.67(ii), §10.67 and Ch.10

►

10.67.15 $$\ker x{\ker }^{\prime }x+\mathrm{kei}x{\mathrm{kei}}^{\prime }x\sim -\frac{\pi }{2x}{\mathrm{e}}^{-x\sqrt{2}}\left(\frac{1}{\sqrt{2}}+\frac{3}{8}\frac{1}{x}-\frac{15}{64\sqrt{2}}\frac{1}{x^2}+\frac{45}{512}\frac{1}{x^3}+\frac{315}{8192\sqrt{2}}\frac{1}{x^4}+\mathrm{\cdots }\right),$$

ⓘ

Symbols:

${\mathrm{kei}}_{\nu }\left(x\right)$: Kelvin function, ${\ker }_{\nu }\left(x\right)$: Kelvin function, $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm and $x$: real variable

A&S Ref:

9.10.33

Permalink:

http://dlmf.nist.gov/10.67.E15

Encodings:

pMML, png, TeX

See also:

Annotations for §10.67(ii), §10.67 and Ch.10

…

7: 10.63 Recurrence Relations and Derivatives

… ►

§10.63(i) ${\mathrm{ber}}_{\nu }x$, ${\mathrm{bei}}_{\nu }x$, ${\ker }_{\nu }x$, ${\mathrm{kei}}_{\nu }x$

… ►

${\ker }_{\nu }x,{\mathrm{kei}}_{\nu }x;$

►

${\mathrm{kei}}_{\nu }x,-{\ker }_{\nu }x.$

… ►

$\sqrt{2}{\ker }^{\prime }x={\ker }_{1}x+{\mathrm{kei}}_{1}x,$

… ►Equations (10.63.6) and (10.63.7) also hold when the symbols $\mathrm{ber}$ and $\mathrm{bei}$ in (10.63.5) are replaced throughout by $\ker$ and $\mathrm{kei}$, respectively. …

8: 12.16 Mathematical Applications

… ►PCFs are also used in integral transforms with respect to the parameter, and inversion formulas exist for kernels containing PCFs. …

9: 10.70 Zeros

… ►

$$\text{zeros of }{\ker }_{\nu }x\sim \sqrt{2}(t+f(-t)),$$ $t=(m-\frac{1}{2}\nu -\frac{5}{8})\pi$,

…

10: 13.27 Mathematical Applications

… ►The other group elements correspond to integral operators whose kernels can be expressed in terms of Whittaker functions. …