Dedekind%20sums

SearchAdvancedHelp

(0.002 seconds)

1—10 of 429 matching pages

1: 27.14 Unrestricted Partitions

… ►and $s(h,k)$ is a Dedekind sum given by … ►

§27.14(iv) Relation to Modular Functions

►Dedekind sums occur in the transformation theory of the Dedekind modular function $\eta \left(\tau \right)$, defined by …where $\epsilon =\exp \left(\pi \mathrm{i}(((a+d)/(12c))-s(d,c))\right)$ and $s(d,c)$ is given by (27.14.11). ►For further properties of the function $\eta \left(\tau \right)$ see §§23.15–23.19. …

2: 23.17 Elementary Properties

… ►

$\eta \left(\mathrm{i}\right)={\displaystyle \frac{\mathrm{\Gamma }\left(\frac{1}{4}\right)}{2{\pi }^{3/4}}},$

►

$\eta \left({\mathrm{e}}^{\pi \mathrm{i}/3}\right)={\displaystyle \frac{3^{1/8}{\left(\mathrm{\Gamma }\left(\frac{1}{3}\right)\right)}^{3/2}}{2\pi }}{\mathrm{e}}^{\pi \mathrm{i}/24}.$

… ►

23.17.6 $$\eta \left(\tau \right)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{(-1)}^n{q}^{{(6n+1)}^2/12}.$$

ⓘ

Symbols:

$\eta \left(\tau \right)$: Dedekind’s eta function (or Dedekind modular function), $q$: nome, $n$: integer and $\tau$: complex variable

Permalink:

http://dlmf.nist.gov/23.17.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §23.17(ii), §23.17 and Ch.23

… ►

23.17.8 $$\eta \left(\tau \right)=q^{1/12}\prod _{n=1}^{\mathrm{\infty }}(1-q^{2n}),$$

ⓘ

Symbols:

$\eta \left(\tau \right)$: Dedekind’s eta function (or Dedekind modular function), $q$: nome, $n$: integer and $\tau$: complex variable

Referenced by:

§23.15(ii), §23.19

Permalink:

http://dlmf.nist.gov/23.17.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §23.17(iii), §23.17 and Ch.23

…

3: 23.18 Modular Transformations

… ►

Dedekind’s Eta Function

►

23.18.5 $$\eta \left(𝒜\tau \right)=\epsilon (𝒜){\left(-\mathrm{i}(c\tau +d)\right)}^{1/2}\eta \left(\tau \right),$$

ⓘ

Symbols:

$\eta \left(\tau \right)$: Dedekind’s eta function (or Dedekind modular function), $\mathrm{i}$: imaginary unit, $\tau$: complex variable, $𝒜$: bilinear transformation, $c$: integer, $d$: integer and $\epsilon (𝒜)$: function

Permalink:

http://dlmf.nist.gov/23.18.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §23.18, §23.18 and Ch.23

… ►

23.18.7 $$s(d,c)=\sum _{r=1}^{c-1}\frac{r}{c}\left(\frac{dr}{c}-\lfloor \frac{dr}{c}\rfloor -\frac{1}{2}\right),$$ $c>0$.

ⓘ

Symbols:

$\lfloor x\rfloor$: floor of $x$ , $\left(m,n\right)$: greatest common divisor (gcd), $c$: integer and $d$: integer

Referenced by:

§23.18, Erratum (V1.0.11) for Equation (23.18.7)

Permalink:

http://dlmf.nist.gov/23.18.E7

Encodings:

pMML, png, TeX

Errata (effective with 1.0.11):

Originally the sum ${\sum }_{r=1}^{c-1}$ was written with an additional constraint on the summation, that $\left(r,c\right)=1$. This additional condition was incorrect and has been removed.

Reported 2015-10-05 by Howard Cohl and Tanay Wakhare

See also:

Annotations for §23.18, §23.18 and Ch.23

►Here $s(d,c)$ is a Dedekind sum. …Note that $\eta \left(\tau \right)$ is of level $\frac{1}{2}$. …

4: 23.16 Graphics

… ►See Figures 23.16.1–23.16.3 for the modular functions $\lambda$, $J$, and $\eta$. … ►

►►

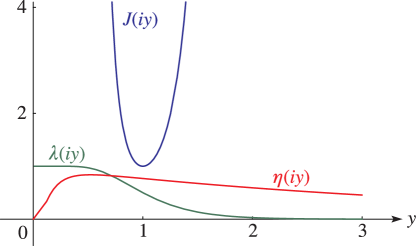
Figure 23.16.1: Modular functions $\lambda \left(\mathrm{i}y\right)$, $J\left(\mathrm{i}y\right)$, $\eta \left(\mathrm{i}y\right)$ for $0\le y\le 3$. … Magnify

… ►

►

►

Figure 23.16.3: Dedekind’s eta function $\eta \left(x+\mathrm{i}y\right)$ for $-0.0625\le x\le 0.0625$, $0.0001\le y\le 0.07$. Magnify 3D Help

5: 23.19 Interrelations

… ►

23.19.1 $$\lambda \left(\tau \right)=16{\left(\frac{{\eta }^2\left(2\tau \right)\eta \left(\frac{1}{2}\tau \right)}{{\eta }^3\left(\tau \right)}\right)}^8,$$

ⓘ

Symbols:

$\eta \left(\tau \right)$: Dedekind’s eta function (or Dedekind modular function), $\lambda \left(\tau \right)$: elliptic modular function and $\tau$: complex variable

Permalink:

http://dlmf.nist.gov/23.19.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §23.19 and Ch.23

… ►

23.19.4 $$\mathrm{\Delta }={(2\pi )}^{12}{\eta }^{24}\left(\tau \right).$$

ⓘ

Symbols:

$\eta \left(\tau \right)$: Dedekind’s eta function (or Dedekind modular function), $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{\Delta }$: discriminant and $\tau$: complex variable

Referenced by:

§23.19

Permalink:

http://dlmf.nist.gov/23.19.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §23.19 and Ch.23

6: 23.15 Definitions

… ►

§23.15(ii) Functions $\lambda \left(\tau \right)$, $J\left(\tau \right)$, $\eta \left(\tau \right)$

… ►

Dedekind’s Eta Function (or Dedekind Modular Function)

►

23.15.9 $$\eta \left(\tau \right)={\left(\frac{1}{2}{\theta }_1^{\prime }(0,q)\right)}^{1/3}={\mathrm{e}}^{\mathrm{i}\pi \tau /12}{\theta }_3\left(\frac{1}{2}\pi (1+\tau )\right|3\tau ).$$

ⓘ

Symbols:

$\eta \left(\tau \right)$: Dedekind’s eta function (or Dedekind modular function), ${\theta }_j(z,q)$: theta function, ${\theta }_j\left(z\right|\tau )$: theta function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $q$: nome and $\tau$: complex variable

Referenced by:

§23.15(ii), §23.15(ii), §23.17(iii)

Permalink:

http://dlmf.nist.gov/23.15.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §23.15(ii), §23.15(ii), §23.15 and Ch.23

…

7: Bibliography R

… ►

On the definition and properties of generalized $6$-$j$ symbols. J. Math. Phys. 20 (12), pp. 2398–2415.

ⓘ

External Links:

ISSN 0022-2488, Document, MathReview (S. Saran), ZentralBlatt

Referenced by:

§16.4(iii), §16.4(iii).

Encodings:

BibTeX

… ►

Infinite Sum of the Incomplete Gamma Function Expressed in Terms of the Hurwitz Zeta Function. Mathematics 9 (16).

ⓘ

External Links:

Link, ISSN 2227-7390, Document

Referenced by:

§8.15.

Encodings:

BibTeX

… ►

Another proof of the triple sum formula for Wigner $9j$-symbols. J. Math. Phys. 40 (12), pp. 6689–6691.

ⓘ

External Links:

ISSN 0022-2488, Document, MathReview (Michael Wüstner), ZentralBlatt

Referenced by:

§34.6.

Encodings:

BibTeX

… ►

Finite-sum rules for Macdonald’s functions and Hankel’s symbols. Integral Transform. Spec. Funct. 10 (2), pp. 115–124.

ⓘ

External Links:

ISSN 1065-2469, Document, MathReview, ZentralBlatt

Referenced by:

§10.60(iii).

Encodings:

BibTeX

… ►

Elliptic and modular functions from Gauss to Dedekind to Hecke. Cambridge University Press, Cambridge.

ⓘ

External Links:

ISBN 978-1-107-15938-9, Document, Link, MathReview (Paul M. Jenkins), ZentralBlatt

Referenced by:

Profile Ranjan Roy.

Encodings:

BibTeX

…

8: Ranjan Roy

… ►He also authored another two advanced mathematics books: Sources in the development of mathematics (Roy, 2011), Elliptic and modular functions from Gauss to Dedekind to Hecke (Roy, 2017). …

9: Bibliography

… ►

Exact linearization of a Painlevé transcendent. Phys. Rev. Lett. 38 (20), pp. 1103–1106.

ⓘ

External Links:

Document, MathReview (Mark Adler)

Referenced by:

§32.11(ii), §32.13(i), §32.13(ii), §32.13(iii), §32.5.

Encodings:

BibTeX

… ►

On the degrees of irreducible factors of higher order Bernoulli polynomials. Acta Arith. 62 (4), pp. 329–342.

ⓘ

External Links:

ISSN 0065-1036, Pdf, MathReview (L. Skula), ZentralBlatt

Referenced by:

§24.12(iii).

Encodings:

BibTeX

… ►

Repeated integrals and derivatives of $K$ Bessel functions. SIAM J. Math. Anal. 20 (1), pp. 169–175.

ⓘ

External Links:

ISSN 0036-1410, Document, MathReview (A. Haimovici), ZentralBlatt

Referenced by:

§10.43(iii).

Encodings:

BibTeX

… ►

Theorems on generalized Dedekind sums. Pacific J. Math. 2 (1), pp. 1–9.

ⓘ

External Links:

MathReview (N. G. de Bruijn), ZentralBlatt

Referenced by:

(25.11.41), (25.11.42), §25.11(xii).

Encodings:

BibTeX

… ►

Bernoulli’s power-sum formulas revisited. Math. Gaz. 90 (518), pp. 276–279.

ⓘ

Referenced by:

§24.4(iii).

Encodings:

BibTeX

…

10: 23.1 Special Notation

… ►The main functions treated in this chapter are the Weierstrass $\mathrm{\wp }$-function $\mathrm{\wp }\left(z\right)=\mathrm{\wp }\left(z|𝕃\right)=\mathrm{\wp }(z;g_2,g_3)$; the Weierstrass zeta function $\zeta \left(z\right)=\zeta \left(z|𝕃\right)=\zeta (z;g_2,g_3)$; the Weierstrass sigma function $\sigma \left(z\right)=\sigma \left(z|𝕃\right)=\sigma (z;g_2,g_3)$; the elliptic modular function $\lambda \left(\tau \right)$; Klein’s complete invariant $J\left(\tau \right)$; Dedekind’s eta function $\eta \left(\tau \right)$. …