Dawson integral

SearchAdvancedHelp

(0.001 seconds)

1—10 of 23 matching pages

1: 7.2 Definitions

… ► $\mathrm{erf}z$, $\mathrm{erfc}z$, and $w\left(z\right)$ are entire functions of $z$, as is $F\left(z\right)$ in the next subsection. … ►

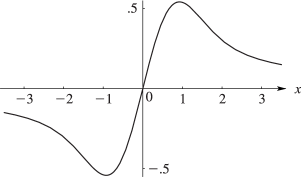
§7.2(ii) Dawson’s Integral

►

7.2.5 $$F\left(z\right)={\mathrm{e}}^{-z^2}{\int }_0^z{\mathrm{e}}^{t^2}dt.$$

ⓘ

Defines:

$F\left(z\right)$: Dawson’s integral

Symbols:

$dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral and $z$: complex variable

A&S Ref:

7.1.1

Permalink:

http://dlmf.nist.gov/7.2.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §7.2(ii), §7.2 and Ch.7

…

2: 7.24 Approximations

… ►

Cody (1968) gives minimax rational approximations for the Fresnel integrals (maximum relative precision 19S); for a Fortran algorithm and comments see Snyder (1993).

►

Cody et al. (1970) gives minimax rational approximations to Dawson’s integral $F\left(x\right)$ (maximum relative precision 20S–22S).

… ►

Luke (1969b, pp. 323–324) covers $\frac{1}{2}\sqrt{\pi }\mathrm{erf}x$ and ${\mathrm{e}}^{x^2}F\left(x\right)$ for $-3\le x\le 3$ (the Chebyshev coefficients are given to 20D); $\sqrt{\pi }x{\mathrm{e}}^{x^2}\mathrm{erfc}x$ and $2xF\left(x\right)$ for $x\ge 3$ (the Chebyshev coefficients are given to 20D and 15D, respectively). Coefficients for the Fresnel integrals are given on pp. 328–330 (20D).

… ►

Shepherd and Laframboise (1981) gives coefficients of Chebyshev series for $(1+2x){\mathrm{e}}^{x^2}\mathrm{erfc}x$ on $(0,\mathrm{\infty })$ (22D).

… ►

Luke (1969b, vol. 2, pp. 422–435) gives main diagonal Padé approximations for $F\left(z\right)$, $\mathrm{erf}z$, $\mathrm{erfc}z$, $C\left(z\right)$, and $S\left(z\right)$; approximate errors are given for a selection of $z$-values.

3: 7.3 Graphics

… ►

►►

Figure 7.3.2: Dawson’s integral $F\left(x\right)$, $-3.5\le x\le 3.5$. Magnify

…

4: 7.8 Inequalities

… ►

7.8.7 $x>0$.

ⓘ

Symbols:

$F\left(z\right)$: Dawson’s integral, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\sinh z$: hyperbolic sine function, $\int$: integral and $x$: real variable

Referenced by:

Erratum (V1.1.5) for Additions

Permalink:

http://dlmf.nist.gov/7.8.E7

Encodings:

pMML, png, TeX

Addition (effective with 1.1.5):

A new inequality was added.

See also:

Annotations for §7.8 and Ch.7

►The function $F\left(x\right)/\sqrt{1-{\mathrm{e}}^{-2x^2}}$ is strictly decreasing for $x>0$. For these and similar results for Dawson’s integral $F\left(x\right)$ see Janssen (2021). …

5: 7.4 Symmetry

… ►

7.4.4 $$F\left(-z\right)=-F\left(z\right).$$

ⓘ

Symbols:

$F\left(z\right)$: Dawson’s integral and $z$: complex variable

Permalink:

http://dlmf.nist.gov/7.4.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §7.4 and Ch.7

…

6: 7.1 Special Notation

… ►Unless otherwise noted, primes indicate derivatives with respect to the argument. ►The main functions treated in this chapter are the error function $\mathrm{erf}z$; the complementary error functions $\mathrm{erfc}z$ and $w\left(z\right)$; Dawson’s integral $F\left(z\right)$; the Fresnel integrals $ℱ\left(z\right)$, $C\left(z\right)$, and $S\left(z\right)$; the Goodwin–Staton integral $G\left(z\right)$; the repeated integrals of the complementary error function ${\mathrm{i}}^n\mathrm{erfc}\left(z\right)$; the Voigt functions $𝖴(x,t)$ and $𝖵(x,t)$. ►Alternative notations are $Q(z)=\frac{1}{2}\mathrm{erfc}\left(z/\sqrt{2}\right)$, $P(z)=\mathrm{\Phi }(z)=\frac{1}{2}\mathrm{erfc}\left(-z/\sqrt{2}\right)$, $\mathrm{Erf}z=\frac{1}{2}\sqrt{\pi }\mathrm{erf}z$, $\mathrm{Erfi}z={\mathrm{e}}^{z^2}F\left(z\right)$, $C_1(z)=C\left(\sqrt{2/\pi }z\right)$, $S_1(z)=S\left(\sqrt{2/\pi }z\right)$, $C_2(z)=C\left(\sqrt{2z/\pi }\right)$, $S_2(z)=S\left(\sqrt{2z/\pi }\right)$. …

7: 7.5 Interrelations

§7.5 Interrelations

►

7.5.1 $$F\left(z\right)=\frac{1}{2}\mathrm{i}\sqrt{\pi }\left({\mathrm{e}}^{-z^2}-w\left(z\right)\right)=-\frac{1}{2}\mathrm{i}\sqrt{\pi }{\mathrm{e}}^{-z^2}\mathrm{erf}\left(\mathrm{i}z\right).$$

ⓘ

Symbols:

$F\left(z\right)$: Dawson’s integral, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{erf}z$: error function, $w\left(z\right)$: Faddeeva (or Faddeyeva) function, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit and $z$: complex variable

Referenced by:

§7.5

Permalink:

http://dlmf.nist.gov/7.5.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §7.5 and Ch.7

… ► ►

7.5.13 $$G\left(x\right)=\sqrt{\pi }F\left(x\right)-\frac{1}{2}{\mathrm{e}}^{-x^2}\mathrm{Ei}\left(x^2\right),$$ $x>0$.

ⓘ

Symbols:

$F\left(z\right)$: Dawson’s integral, $G\left(z\right)$: Goodwin–Staton integral, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{Ei}\left(x\right)$: exponential integral and $x$: real variable

Referenced by:

§7.5

Permalink:

http://dlmf.nist.gov/7.5.E13

Encodings:

pMML, png, TeX

See also:

Annotations for §7.5 and Ch.7

…

8: 7.23 Tables

… ►

Abramowitz and Stegun (1964, Chapter 7) includes $\mathrm{erf}x$, $(2/\sqrt{\pi }){\mathrm{e}}^{-x^2}$, $x\in [0,2]$, 10D; $(2/\sqrt{\pi }){\mathrm{e}}^{-x^2}$, $x\in [2,10]$, 8S; $x{\mathrm{e}}^{x^2}\mathrm{erfc}x$, $x^{-2}\in [0,0.25]$, 7D; $2^n\mathrm{\Gamma }\left(\frac{1}{2}n+1\right){\mathrm{i}}^n\mathrm{erfc}\left(x\right)$, $n=1(1)6,10,11$, $x\in [0,5]$, 6S; $F\left(x\right)$, $x\in [0,2]$, 10D; $xF\left(x\right)$, $x^{-2}\in [0,0.25]$, 9D; $C\left(x\right)$, $S\left(x\right)$, $x\in [0,5]$, 7D; $\mathrm{f}\left(x\right)$, $\mathrm{g}\left(x\right)$, $x\in [0,1]$, $x^{-1}\in [0,1]$, 15D.

… ►

Zhang and Jin (1996, pp. 637, 639) includes $(2/\sqrt{\pi }){\mathrm{e}}^{-x^2}$, $\mathrm{erf}x$, $x=0(.02)1(.04)3$, 8D; $C\left(x\right)$, $S\left(x\right)$, $x=0(.2)10(2)100(100)500$, 8D.

…

9: 8.4 Special Values

… ►For $\mathrm{erf}\left(z\right)$, $\mathrm{erfc}\left(z\right)$, and $F\left(z\right)$, see §§7.2(i), 7.2(ii). … ►

8.4.3 $${\gamma }^{\ast }(\frac{1}{2},-z^2)=\frac{2{\mathrm{e}}^{z^2}}{z\sqrt{\pi }}F\left(z\right).$$

ⓘ

Symbols:

$F\left(z\right)$: Dawson’s integral, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, ${\gamma }^{\ast }(a,z)$: incomplete gamma function and $z$: complex variable

A&S Ref:

6.5.18

Permalink:

http://dlmf.nist.gov/8.4.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §8.4 and Ch.8

…

10: 7.16 Generalized Error Functions

§7.16 Generalized Error Functions

►Generalizations of the error function and Dawson’s integral are ${\int }_0^x{\mathrm{e}}^{-t^p}dt$ and ${\int }_0^x{\mathrm{e}}^{t^p}dt$. …