Askey–Wilson polynomials

SearchAdvancedHelp

(0.005 seconds)

1—10 of 26 matching pages

1: 18.29 Asymptotic Approximations for $q$-Hahn and Askey–Wilson Classes

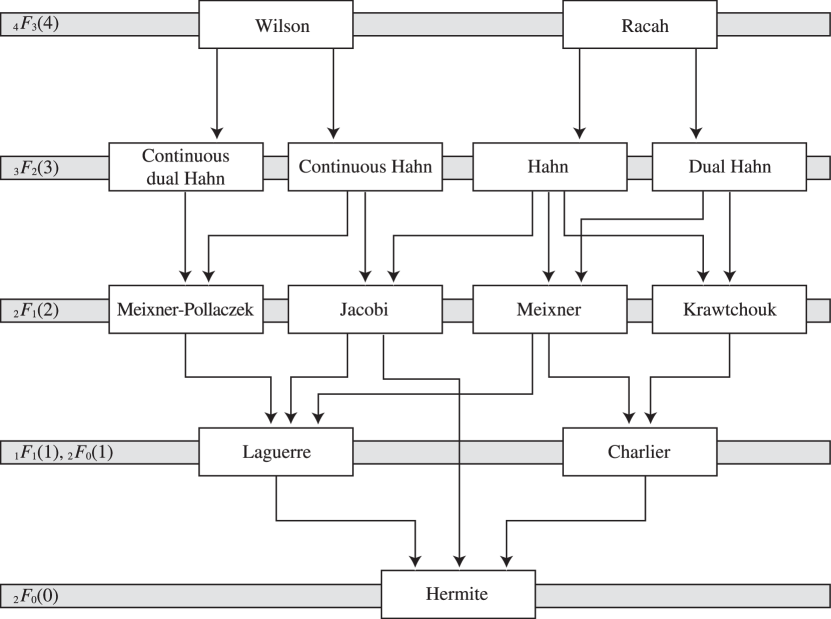
§18.29 Asymptotic Approximations for $q$-Hahn and Askey–Wilson Classes

►Ismail (1986) gives asymptotic expansions as $n\to \mathrm{\infty }$, with $x$ and other parameters fixed, for continuous $q$-ultraspherical, big and little $q$-Jacobi, and Askey–Wilson polynomials. …For Askey–Wilson $p_n(\cos \theta ;a,b,c,d|q)$ the leading term is given by …

2: 18.28 Askey–Wilson Class

… ►

§18.28(ii) Askey–Wilson Polynomials

… ►The polynomials $p_n(x;a,b,c,d|q)$ are symmetric in the parameters $a,b,c,d$. … ►

Recurrence Relation

… ►

Duality

… ►

18.28.29 $$\underset{q\to 1}{lim}\frac{p_n(1-\frac{1}{2}x{(1-q)}^2;q^a,q^b,q^c,q^d|q)}{{(1-q)}^{3n}}=W_n(x;a,b,c,d).$$

ⓘ

Symbols:

$p_n(x;a,b,c,d|q)$: Askey–Wilson polynomial, $W_n(x;a,b,c,d)$: Wilson polynomial, $q$: real variable, $n$: nonnegative integer and $x$: real variable

Proof sketch:

Substitute (18.28.1) in the left-hand side, take the limit, and use (18.26.1).

Notes:

Another form of this limit is given in Koekoek et al. (2010, (14.1.21)).

Referenced by:

§18.28(x)

Permalink:

http://dlmf.nist.gov/18.28.E29

Encodings:

pMML, png, TeX

See also:

Annotations for §18.28(x), §18.28(x), §18.28 and Ch.18

…

3: 18.1 Notation

… ►

Askey–Wilson: $p_n(x;a,b,c,d|q)$.

…

4: Tom H. Koornwinder

… ►Koornwinder has published numerous papers on special functions, harmonic analysis, Lie groups, quantum groups, computer algebra, and their interrelations, including an interpretation of Askey–Wilson polynomials on quantum SU(2), and a five-parameter extension (the Macdonald–Koornwinder polynomials) of Macdonald’s polynomials for root systems BC. …

5: Richard A. Askey

… ► Wilson), introduced the Askey-Wilson polynomials. …

6: 18.38 Mathematical Applications

… ►If we consider this abstract algebra with additional relation (18.38.9) and with dependence on $a,b,c,d$ according to (18.38.7) then it is isomorphic with the algebra generated by $K_0=L$ given by (18.28.6_2), $(K_{1}f)(z)=(z+z^{-1})f(z)$ and $K_2$ given by (18.38.4), and $K_0,K_1,K_2$ act on the linear span of the Askey–Wilson polynomials (18.28.1). See Zhedanov (1991), Granovskiĭ et al. (1992, §3), Koornwinder (2007a, §2) and Terwilliger (2011). … ►The Dunkl type operator is a $q$-difference-reflection operator acting on Laurent polynomials and its eigenfunctions, the nonsymmetric Askey–Wilson polynomials, are linear combinations of the symmetric Laurent polynomial $R_n(z;a,b,c,d|q)$ and the ‘anti-symmetric’ Laurent polynomial $z^{-1}(1-az)(1-bz)R_{n-1}(z;qa,qb,c,d|q)$, where $R_n(z)$ is given in (18.28.1_5). … ►Dunkl type operators and nonsymmetric polynomials have been associated with various other families in the Askey scheme and $q$-Askey scheme, in particular with Wilson polynomials, see Groenevelt (2007), and with Jacobi polynomials, see Koornwinder and Bouzeffour (2011, §7). …

7: Bibliography K

… ►

Nonsymmetric Askey-Wilson polynomials as vector-valued polynomials. Appl. Anal. 90 (3-4), pp. 731–746.

ⓘ

External Links:

ISSN 0003-6811, Link, MathReview (Masatoshi Iida), ZentralBlatt

Referenced by:

§18.38(iii), §18.38(iii).

Encodings:

BibTeX

… ►

Askey-Wilson Polynomials for Root Systems of Type $BC$ . In Hypergeometric Functions on Domains of Positivity, Jack Polynomials, and Applications (Tampa, FL, 1991), Contemp. Math., Vol. 138, pp. 189–204.

ⓘ

External Links:

FullText, MathReview (Eric M. Opdam), ZentralBlatt

Referenced by:

§18.37(iii).

Encodings:

BibTeX

►

Askey-Wilson polynomials as zonal spherical functions on the $\mathrm{SU}(2)$ quantum group. SIAM J. Math. Anal. 24 (3), pp. 795–813.

ⓘ

External Links:

ISSN 0036-1410, Document, Link, MathReview Entry

Referenced by:

(18.28.27).

Encodings:

BibTeX

… ►

The structure relation for Askey-Wilson polynomials. J. Comput. Appl. Math. 207 (2), pp. 214–226.

ⓘ

External Links:

ISSN 0377-0427, Document, Link, MathReview Entry

Referenced by:

(18.9.18_5).

Encodings:

BibTeX

… ►

Askey-Wilson polynomial. Scholarpedia 7 (7), pp. 7761.

ⓘ

Notes:

Electronic only

External Links:

Document, FullText

Referenced by:

§18.28(i), §18.28(i).

Encodings:

BibTeX

…

8: Bibliography Z

… ►

“Hidden symmetry” of Askey-Wilson polynomials. Theoret. and Math. Phys. 89 (2), pp. 1146–1157.

ⓘ

External Links:

MathReview (Vadim B. Kuznetsov), ZentralBlatt

Referenced by:

§18.38(iii).

Encodings:

BibTeX

…

9: Errata

… ►

18.28.1 $$p_n(x)=p_n(x;a,b,c,d|q)=a^{-n}\sum _{\mathrm{\ell }=0}^n{q}^{\mathrm{\ell }}{(ab{q}^{\mathrm{\ell }},ac{q}^{\mathrm{\ell }},ad{q}^{\mathrm{\ell }};q)}_{n-\mathrm{\ell }}\frac{{(q^{-n},abcd{q}^{n-1};q)}_{\mathrm{\ell }}}{{(q;q)}_{\mathrm{\ell }}}\prod _{j=0}^{\mathrm{\ell }-1}(1-2a{q}^{j}x+a^2{q}^{2j}),$$

18.28.1_5 $$R_n(z)=R_n(z;a,b,c,d|q)=\frac{p_n(\frac{1}{2}(z+z^{-1});a,b,c,d|q)}{a^{-n}{(ab,ac,ad;q)}_n}={}_4{}^{}\varphi _3^{}(\genfrac{}{}{0pt}{}{q^{-n},abcd{q}^{n-1},az,a{z}^{-1}}{ab,ac,ad};q,q)$$

Previously we presented all the information of these formulas in one equation

$$p_n(\cos \theta )=p_n(\cos \theta ;a,b,c,d|q)=a^{-n}\sum _{\mathrm{\ell }=0}^n{q}^{\mathrm{\ell }}{(ab{q}^{\mathrm{\ell }},ac{q}^{\mathrm{\ell }},ad{q}^{\mathrm{\ell }};q)}_{n-\mathrm{\ell }}\frac{{(q^{-n},abcd{q}^{n-1};q)}_{\mathrm{\ell }}}{{(q;q)}_{\mathrm{\ell }}}\prod _{j=0}^{\mathrm{\ell }-1}(1-2a{q}^j\cos \theta +a^2{q}^{2j})=a^{-n}{(ab,ac,ad;q)}_n{}_4{}^{}\varphi _3^{}(\genfrac{}{}{0pt}{}{q^{-n},abcd{q}^{n-1},a{\mathrm{e}}^{\mathrm{i}\theta },a{\mathrm{e}}^{-\mathrm{i}\theta }}{ab,ac,ad};q,q).$$

…

10: 18.21 Hahn Class: Interrelations

… ►

►►

Figure 18.21.1: Askey scheme. … Magnify