Askey–Wilson class orthogonal polynomials

SearchAdvancedHelp

(0.010 seconds)

1—10 of 13 matching pages

1: 18.29 Asymptotic Approximations for $q$-Hahn and Askey–Wilson Classes

§18.29 Asymptotic Approximations for $q$-Hahn and Askey–Wilson Classes

…

2: 18.28 Askey–Wilson Class

§18.28 Askey–Wilson Class

… ► … ►

§18.28(ii) Askey–Wilson Polynomials

… ►

§18.28(viii) $q$-Racah Polynomials

… ►Genest et al. (2016) showed that these polynomials coincide with the nonsymmetric Wilson polynomials in Groenevelt (2007).

3: 18.21 Hahn Class: Interrelations

… ►

►►

Figure 18.21.1: Askey scheme. … Magnify

4: 18.26 Wilson Class: Continued

… ►Moreover, if one or more of the new parameters becomes zero, then the polynomial descends to a lower family in the Askey scheme.

5: 18.38 Mathematical Applications

… ► … ► … ►See Zhedanov (1991), Granovskiĭ et al. (1992, §3), Koornwinder (2007a, §2) and Terwilliger (2011). … ►The Dunkl type operator is a $q$-difference-reflection operator acting on Laurent polynomials and its eigenfunctions, the nonsymmetric Askey–Wilson polynomials, are linear combinations of the symmetric Laurent polynomial $R_n(z;a,b,c,d|q)$ and the ‘anti-symmetric’ Laurent polynomial $z^{-1}(1-az)(1-bz)R_{n-1}(z;qa,qb,c,d|q)$, where $R_n(z)$ is given in (18.28.1_5). … ►Dunkl type operators and nonsymmetric polynomials have been associated with various other families in the Askey scheme and $q$-Askey scheme, in particular with Wilson polynomials, see Groenevelt (2007), and with Jacobi polynomials, see Koornwinder and Bouzeffour (2011, §7). …

6: Bibliography Z

… ►

The Dilogarithm Function in Geometry and Number Theory. In Number Theory and Related Topics (Bombay, 1988), R. Askey and others (Eds.), Tata Inst. Fund. Res. Stud. Math., Vol. 12, pp. 231–249.

ⓘ

External Links:

MathReview (J. Browkin), ZentralBlatt

Referenced by:

§25.12(i).

Encodings:

BibTeX

… ►

Doron Zeilberger’s Maple Packages and Programs Department of Mathematics, Rutgers University, New Jersey.

ⓘ

Notes:

Includes hypergeometric and $q$-hypergeometric summation, solution of difference equations (for example, by Petkovšek’s algorithm), combinatorial algorithms, and (package LUC) evaluation of zonal polynomials.

External Links:

Home Page

Referenced by:

§ ‣ Software Cross Index, § ‣ Software Cross Index, L. Lapointe and L. Vinet (1996).

Encodings:

BibTeX

… ►

Weighted derangements and the linearization coefficients of orthogonal Sheffer polynomials. Proc. London Math. Soc. (3) 65 (1), pp. 1–22.

ⓘ

External Links:

ISSN 0024-6115, Document, Link, MathReview (R. A. Askey), ZentralBlatt

Referenced by:

§18.18(v).

Encodings:

BibTeX

… ►

“Hidden symmetry” of Askey-Wilson polynomials. Theoret. and Math. Phys. 89 (2), pp. 1146–1157.

ⓘ

External Links:

MathReview (Vadim B. Kuznetsov), ZentralBlatt

Referenced by:

§18.38(iii).

Encodings:

BibTeX

►

On some classes of polynomials orthogonal on arcs of the unit circle connected with symmetric orthogonal polynomials on an interval. J. Approx. Theory 94 (1), pp. 73–106.

ⓘ

External Links:

ISSN 0021-9045, Link, MathReview (T. S. Chihara), ZentralBlatt

Referenced by:

§18.33(iii).

Encodings:

BibTeX

…

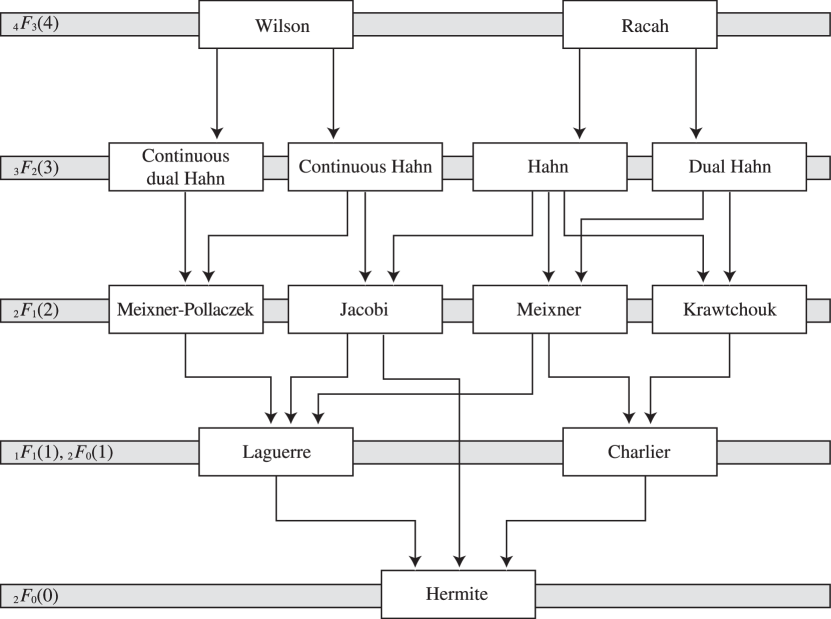
7: 18.27 $q$-Hahn Class

§18.27 $q$-Hahn Class

… ►The $q$-hypergeometric OP’s comprise the $q$-Hahn class (or $q$-linear lattice class) OP’s and the Askey–Wilson class (or $q$-quadratic lattice class) OP’s (§18.28). … ►All these systems of OP’s have orthogonality properties of the form … ►

From Big $q$-Jacobi to Jacobi

… ►

Limit Relations

…

8: 18.22 Hahn Class: Recurrence Relations and Differences

§18.22 Hahn Class: Recurrence Relations and Differences

►

§18.22(i) Recurrence Relations in $n$

… ►These polynomials satisfy (18.22.2) with $p_n(x)$, $A_n$, and $C_n$ as in Table 18.22.1. … ►

§18.22(ii) Difference Equations in $x$

… ►

§18.22(iii) $x$-Differences

…

9: 18.19 Hahn Class: Definitions

§18.19 Hahn Class: Definitions

… ►

Wilson class (or quadratic lattice class). These are OP’s $p_n(x)=p_n(\lambda (y))$ ($p_n(x)$ of degree $n$ in $x$, $\lambda (y)$ quadratic in $y$) where the role of the differentiation operator is played by $\frac{{\mathrm{\Delta }}_y}{{\mathrm{\Delta }}_y(\lambda (y))}$ or $\frac{{\nabla }_y}{{\nabla }_y(\lambda (y))}$ or $\frac{{\delta }_y}{{\delta }_y(\lambda (y))}$. The Wilson class consists of two discrete and two continuous families.

… ►

Hahn, Krawtchouk, Meixner, and Charlier

… ►These polynomials are orthogonal on $(-\mathrm{\infty },\mathrm{\infty })$, and are defined as follows. …A special case of (18.19.8) is $w^{(1/2)}(x;\pi /2)=\frac{\pi }{\cosh \left(\pi x\right)}$.

10: 18.1 Notation

… ►

Hahn Class OP’s

… ►

Wilson Class OP’s

►

Wilson: $W_n(x;a,b,c,d)$.

… ►

Askey–Wilson Class OP’s

►

Askey–Wilson: $p_n(x;a,b,c,d|q)$.

…