Askey polynomials

SearchAdvancedHelp

(0.005 seconds)

1—10 of 44 matching pages

1: 18.29 Asymptotic Approximations for $q$-Hahn and Askey–Wilson Classes

§18.29 Asymptotic Approximations for $q$-Hahn and Askey–Wilson Classes

►Ismail (1986) gives asymptotic expansions as $n\to \mathrm{\infty }$, with $x$ and other parameters fixed, for continuous $q$-ultraspherical, big and little $q$-Jacobi, and Askey–Wilson polynomials. …For Askey–Wilson $p_n(\cos \theta ;a,b,c,d|q)$ the leading term is given by …

2: 18.28 Askey–Wilson Class

… ►

§18.28(ii) Askey–Wilson Polynomials

… ►The polynomials $p_n(x;a,b,c,d|q)$ are symmetric in the parameters $a,b,c,d$. … ►

Recurrence Relation

… ►

Duality

… ►

§18.28(viii) $q$-Racah Polynomials

…

3: 18.1 Notation

… ►

Askey–Wilson: $p_n(x;a,b,c,d|q)$.

…

4: Tom H. Koornwinder

… ►Koornwinder has published numerous papers on special functions, harmonic analysis, Lie groups, quantum groups, computer algebra, and their interrelations, including an interpretation of Askey–Wilson polynomials on quantum SU(2), and a five-parameter extension (the Macdonald–Koornwinder polynomials) of Macdonald’s polynomials for root systems BC. …

5: 18.38 Mathematical Applications

… ►The Askey–Gasper inequality … ►If we consider this abstract algebra with additional relation (18.38.9) and with dependence on $a,b,c,d$ according to (18.38.7) then it is isomorphic with the algebra generated by $K_0=L$ given by (18.28.6_2), $(K_{1}f)(z)=(z+z^{-1})f(z)$ and $K_2$ given by (18.38.4), and $K_0,K_1,K_2$ act on the linear span of the Askey–Wilson polynomials (18.28.1). See Zhedanov (1991), Granovskiĭ et al. (1992, §3), Koornwinder (2007a, §2) and Terwilliger (2011). … ►The Dunkl type operator is a $q$-difference-reflection operator acting on Laurent polynomials and its eigenfunctions, the nonsymmetric Askey–Wilson polynomials, are linear combinations of the symmetric Laurent polynomial $R_n(z;a,b,c,d|q)$ and the ‘anti-symmetric’ Laurent polynomial $z^{-1}(1-az)(1-bz)R_{n-1}(z;qa,qb,c,d|q)$, where $R_n(z)$ is given in (18.28.1_5). … ►Dunkl type operators and nonsymmetric polynomials have been associated with various other families in the Askey scheme and $q$-Askey scheme, in particular with Wilson polynomials, see Groenevelt (2007), and with Jacobi polynomials, see Koornwinder and Bouzeffour (2011, §7). …

6: 18.33 Polynomials Orthogonal on the Unit Circle

… ►

Szegő–Askey

… ►Askey (1982a) and Sri Ranga (2010) give more general results leading to what seem to be the right analogues of Jacobi polynomials on the unit circle. ►

Askey

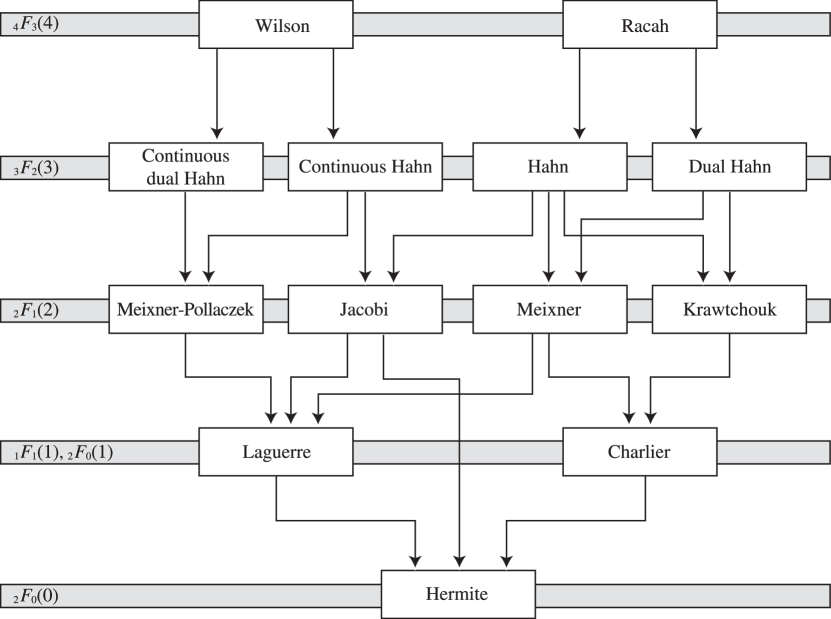
… ► See for a more general class Costa et al. (2012). …

7: 18.21 Hahn Class: Interrelations

… ►

►►

Figure 18.21.1: Askey scheme. … Magnify

8: Richard A. Askey

… ► Wilson), introduced the Askey-Wilson polynomials. Published in 1985 in the Memoirs of the American Mathematical Society, it also introduced the directed graph of hypergeometric orthogonal polynomials commonly known as the Askey scheme. Another significant contribution was the Askey-Gasper inequality for Jacobi polynomials which was published in Positive Jacobi polynomial sums. II (with G. … ►Additional books for which Askey served as author or editor include Orthogonal Polynomials and Special Functions, published by SIAM in 1975, Theory and application of special functions, published by Academic Press in 1975, Special Functions: Group Theoretical Aspects and Applications (with T. … ►Askey was presented a Lifetime Achievement Award in Recognition and Appreciation for his Outstanding Work and Leadership in the Field of Special Functions at the International Symposium on Orthogonal Polynomials, Special Functions and Applications in Hagenberg, Austria on July 24, 2019. …

9: Bibliography K

… ►

Nonsymmetric Askey-Wilson polynomials as vector-valued polynomials. Appl. Anal. 90 (3-4), pp. 731–746.

ⓘ

External Links:

ISSN 0003-6811, Link, MathReview (Masatoshi Iida), ZentralBlatt

Referenced by:

§18.38(iii), §18.38(iii).

Encodings:

BibTeX

… ►

Askey-Wilson Polynomials for Root Systems of Type $BC$ . In Hypergeometric Functions on Domains of Positivity, Jack Polynomials, and Applications (Tampa, FL, 1991), Contemp. Math., Vol. 138, pp. 189–204.

ⓘ

External Links:

FullText, MathReview (Eric M. Opdam), ZentralBlatt

Referenced by:

§18.37(iii).

Encodings:

BibTeX

►

Askey-Wilson polynomials as zonal spherical functions on the $\mathrm{SU}(2)$ quantum group. SIAM J. Math. Anal. 24 (3), pp. 795–813.

ⓘ

External Links:

ISSN 0036-1410, Document, Link, MathReview Entry

Referenced by:

(18.28.27).

Encodings:

BibTeX

… ►

The structure relation for Askey-Wilson polynomials. J. Comput. Appl. Math. 207 (2), pp. 214–226.

ⓘ

External Links:

ISSN 0377-0427, Document, Link, MathReview Entry

Referenced by:

(18.9.18_5).

Encodings:

BibTeX

… ►

Askey-Wilson polynomial. Scholarpedia 7 (7), pp. 7761.

ⓘ

Notes:

Electronic only

External Links:

Document, FullText

Referenced by:

§18.28(i), §18.28(i).

Encodings:

BibTeX

…

10: Bibliography

… ►

Associated Laguerre and Hermite polynomials. Proc. Roy. Soc. Edinburgh 96A, pp. 15–37.

ⓘ

External Links:

MathReview Entry

Referenced by:

(18.30.16), (18.30.17), (18.30.18), (18.30.19), (18.30.20), §18.30(iii), §18.30(iv), §18.30, §18.30(v), (18.35.10).

Encodings:

BibTeX

… ►

Recurrence relations, continued fractions, and orthogonal polynomials. Mem. Amer. Math. Soc. 49 (300), pp. iv+108.

ⓘ

External Links:

ISSN 0065-9266, MathReview (W. A. Al-Salam), ZentralBlatt

Referenced by:

§18.28(iv).

Encodings:

BibTeX

… ►

An integral for Jacobi polynomials. Simon Stevin 46, pp. 165–169.

ⓘ

External Links:

MathReview (H. M. Srivastava), ZentralBlatt

Referenced by:

§18.17(viii).

Encodings:

BibTeX

►

Some basic hypergeometric orthogonal polynomials that generalize Jacobi polynomials. Mem. Amer. Math. Soc. 54 (319), pp. iv+55.

ⓘ

External Links:

ISSN 0065-9266, MathReview (Mourad E. H. Ismail), ZentralBlatt

Referenced by:

§18.21(ii), §18.22(ii), (18.28.24), §18.28(ii), Ch.18, Profile Richard A. Askey.

Encodings:

BibTeX

… ►

Continuous Hahn polynomials. J. Phys. A 18 (16), pp. L1017–L1019.

ⓘ

External Links:

ISSN 0305-4470, FullText, MathReview (T. S. Chihara), ZentralBlatt

Referenced by:

§18.19, §18.20(ii), §18.21(ii).

Encodings:

BibTeX

…