Anger–Weber functions

SearchAdvancedHelp

(0.004 seconds)

1—10 of 11 matching pages

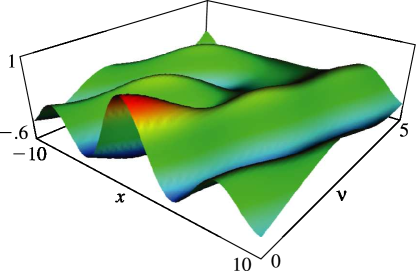
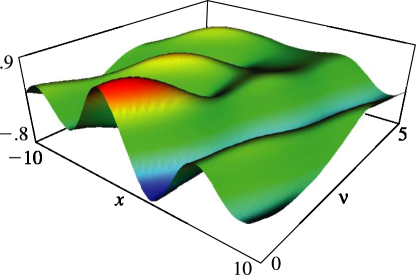
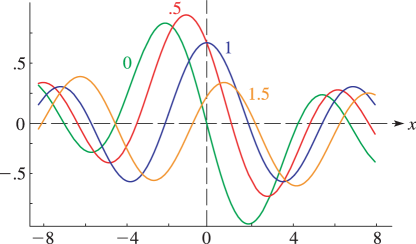
1: 11.10 Anger–Weber Functions

§11.10 Anger–Weber Functions

… ►

►►

Figure 11.10.1: Anger function ${𝐉}_{\nu }\left(x\right)$ for $-8\le x\le 8$ and $\nu =0,\frac{1}{2},1,\frac{3}{2}$. Magnify

►

►►

Figure 11.10.2: Weber function ${𝐄}_{\nu }\left(x\right)$ for $-8\le x\le 8$ and $\nu =0,\frac{1}{2},1,\frac{3}{2}$. Magnify

►

►

►

Figure 11.10.3: Anger function ${𝐉}_{\nu }\left(x\right)$ for $-10\le x\le 10$ and $0\le \nu \le 5$. Magnify 3D Help

►

►

►

Figure 11.10.4: Weber function ${𝐄}_{\nu }\left(x\right)$ for $-10\le x\le 10$ and $0\le \nu \le 5$. Magnify 3D Help

…

2: 11.1 Special Notation

§11.1 Special Notation

… ►For the functions $J_{\nu }\left(z\right)$, $Y_{\nu }\left(z\right)$, $H_{\nu }^{(1)}\left(z\right)$, $H_{\nu }^{(2)}\left(z\right)$, $I_{\nu }\left(z\right)$, and $K_{\nu }\left(z\right)$ see §§10.2(ii), 10.25(ii). ►The functions treated in this chapter are the Struve functions ${𝐇}_{\nu }\left(z\right)$ and ${𝐊}_{\nu }\left(z\right)$, the modified Struve functions ${𝐋}_{\nu }\left(z\right)$ and ${𝐌}_{\nu }\left(z\right)$, the Lommel functions $s_{\mu ,\nu }\left(z\right)$ and $S_{\mu ,\nu }\left(z\right)$, the Anger function ${𝐉}_{\nu }\left(z\right)$, the Weber function ${𝐄}_{\nu }\left(z\right)$, and the associated Anger–Weber function ${𝐀}_{\nu }\left(z\right)$.

3: 11.14 Tables

… ►

§11.14(iv) Anger–Weber Functions

… ►

§11.14(v) Incomplete Functions

►

Agrest and Maksimov (1971, Chapter 11) defines incomplete Struve, Anger, and Weber functions and includes tables of an incomplete Struve function ${𝐇}_n\left(x,\alpha \right)$ for $n=0,1$, $x=0(.2)10$, and $\alpha =0(.2)1.4,\frac{1}{2}\pi$, together with surface plots.

4: 11.11 Asymptotic Expansions of Anger–Weber Functions

§11.11 Asymptotic Expansions of Anger–Weber Functions

►

§11.11(i) Large $|z|$, Fixed $\nu$

… ► ►

§11.11(ii) Large $|\nu |$, Fixed $z$

… ►

11.11.17 $${𝐀}_{-\nu }\left(\nu +a{\nu }^{1/3}\right)=2^{1/3}{\nu }^{-1/3}\mathrm{Hi}\left(-2^{1/3}a\right)+O\left({\nu }^{-1}\right),$$

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $\mathrm{Hi}\left(z\right)$: Scorer function (inhomogeneous Airy function), ${𝐀}_{\nu }\left(z\right)$: Anger–Weber function, $\nu$: real or complex order and $a_k(\lambda )$: expansion function

Sources:

Olver (1997b, pp. 103 and 352); Nemes (2020)

Referenced by:

§11.11(iii), §11.11(iii), §11.11(iii)

Permalink:

http://dlmf.nist.gov/11.11.E17

Encodings:

pMML, png, TeX

See also:

Annotations for §11.11(iii), §11.11 and Ch.11

…

5: 11.13 Methods of Computation

… ►

§11.13(i) Introduction

… ►The treatment of Lommel and Anger–Weber functions is similar. …

6: 11.16 Software

… ►

§11.16(v) Anger and Weber Functions

… ►

§11.16(vi) Integrals of Anger and Weber Functions

…

7: Bibliography N

… ►

The resurgence properties of the large order asymptotics of the Anger-Weber function I. J. Class. Anal. 4 (1), pp. 1–39.

ⓘ

External Links:

ISSN 1848-5979, Document, Link, MathReview (José Luis López)

Referenced by:

(11.11.10), (11.11.8), §11.11(iii).

Encodings:

BibTeX

►

The resurgence properties of the large order asymptotics of the Anger-Weber function II. J. Class. Anal. 4 (2), pp. 121–147.

ⓘ

External Links:

ISSN 1848-5979, Document, Link, MathReview Entry

Referenced by:

(11.11.10), (11.11.8), §11.11(iii).

Encodings:

BibTeX

…

8: 3.6 Linear Difference Equations

… ►

Example 2. Weber Function

…

9: Bibliography B

… ►

Tables of the Anger and Lommel-Weber Functions. Technical report Technical Report 53 and AFCRL 796, University Washington Press, Seattle.

ⓘ

Notes:

Reviewed in Math. Comp., v. 17 (1963), pp.315–317.

Referenced by:

1st item.

Encodings:

BibTeX

…

10: Software Index

… ► ►►►

	Open Source													With Book						Commercial
…
11.16(v) ${𝐉}_{\nu }\left(z\right)$, ${𝐄}_{\nu }\left(z\right)$, ${𝐀}_{\nu }\left(z\right)$												a	✓				✓				✓	✓	a
…

►‘✓’ indicates that a software package implements the functions in a section; ‘a’ indicates available functionality through optional or add-on packages; an empty space indicates no known support. … ►In the list below we identify four main sources of software for computing special functions. … ►

Such software ranges from a collection of reusable software parts (e.g., a library) to fully functional interactive computing environments with an associated computing language. Such software is usually professionally developed, tested, and maintained to high standards. It is available for purchase, often with accompanying updates and consulting support.

… ►The following are web-based software repositories with significant holdings in the area of special functions. …