§8.19 Generalized Exponential Integral
Contents
- §8.19(i) Definition and Integral Representations
- §8.19(ii) Graphics
- §8.19(iii) Special Values
- §8.19(iv) Series Expansions
- §8.19(v) Recurrence Relation and Derivatives
- §8.19(vi) Relation to Confluent Hypergeometric Function
- §8.19(vii) Continued Fraction
- §8.19(viii) Analytic Continuation
- §8.19(ix) Inequalities
- §8.19(x) Integrals
- §8.19(xi) Further Generalizations
§8.19(i) Definition and Integral Representations
For
| 8.19.1 | |||
Most properties of follow straightforwardly from those of . For an extensive treatment of see Chapter 6.
| 8.19.2 | |||
When the path of integration excludes the origin and does not cross the negative real axis (8.19.2) defines the principal value of , and unless indicated otherwise in the DLMF principal values are assumed.
Other Integral Representations
| 8.19.3 | ||||
| , | ||||
| 8.19.4 | ||||
| , . | ||||
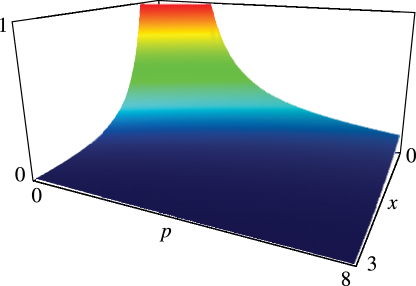
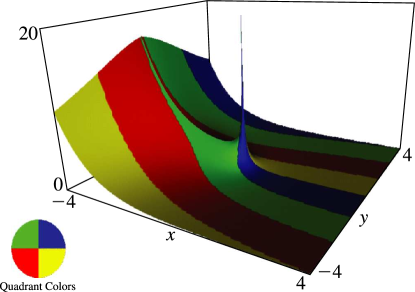
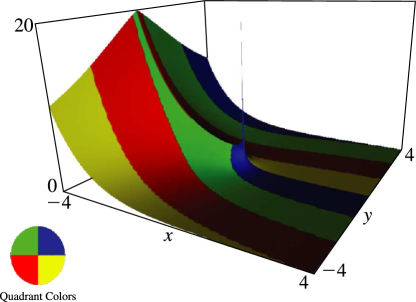
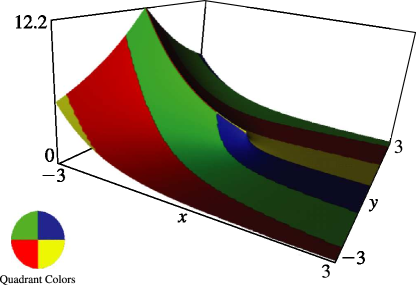
§8.19(ii) Graphics
In Figures 8.19.2–8.19.5, height corresponds to the absolute value of the function and color to the phase. See About Color Map.
§8.19(iii) Special Values
| 8.19.5 | |||
| , | |||
| 8.19.6 | |||
| , | |||
| 8.19.7 | |||
| . | |||
§8.19(iv) Series Expansions
When
| 8.19.10 | |||
| 8.19.11 | |||
again with in both equations. The right-hand sides are replaced by their limiting forms when .
§8.19(v) Recurrence Relation and Derivatives
| 8.19.12 | |||
| 8.19.13 | ||||
| 8.19.14 | ||||
-Derivatives
§8.19(vi) Relation to Confluent Hypergeometric Function
| 8.19.16 | |||
For see §13.2(i).
§8.19(vii) Continued Fraction
| 8.19.17 | |||
| . | |||
See also Cuyt et al. (2008, pp. 277–285).
§8.19(viii) Analytic Continuation
The general function is attained by extending the path in (8.19.2) across the negative real axis. Unless is a nonpositive integer, has a branch point at . For each branch of is an entire function of .
| 8.19.18 | |||
| , . | |||
§8.19(ix) Inequalities
For and ,
| 8.19.19 | |||
| 8.19.20 | |||
| 8.19.21 | |||
| 8.19.22 | |||