10 Bessel Functions Bessel and Hankel Functions 10.19 Asymptotic Expansions for Large Order 10.21 Zeros

§10.20 Uniform Asymptotic Expansions for Large Order

Keywords:: Bessel functions, Hankel functions
Referenced by:: §10.41(v), §10.57, §2.8(iii)
Permalink:: http://dlmf.nist.gov/10.20

§10.20(i) Real Variables
§10.20(ii) Complex Variables
§10.20(iii) Double Asymptotic Properties

§10.20(i) Real Variables

Notes:: See Olver (1997b, pp. 419–425).
Keywords:: Bessel functions, Hankel functions, derivatives
Referenced by:: §10.20(ii), §10.74(i), §10.74(ii), §10.75(ii)
Permalink:: http://dlmf.nist.gov/10.20.i

Define $\zeta=\zeta(z)$ to be the solution of the differential equation

10.20.1 $\left(\frac{d\zeta}{dz}\right)^{2}=\frac{1-z^{2}}{\zeta z^{2}}$

Symbols:: $\frac{df}{dx}$ : derivative of with respect to , : complex variable and $\zeta(z)$ : solution
Permalink:: http://dlmf.nist.gov/10.20.E1
Encodings:: TeX, pMML, png

that is infinitely differentiable on the interval $0<z<\infty$ , including . Then

10.20.2 $\frac{2}{3}\zeta^{{\frac{3}{2}}}=\int_{z}^{1}\frac{\sqrt{1-t^{2}}}{t}dt=% \mathop{\ln\/}\nolimits\!\left(\frac{1+\sqrt{1-z^{2}}}{z}\right)-\sqrt{1-z^{2}},$ $0<z\leq 1$ ,

Symbols:: : differential of , $\int$ : integral, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, : complex variable and $\zeta(z)$ : solution
A&S Ref:: 9.3.38
Referenced by:: §10.20(ii)
Permalink:: http://dlmf.nist.gov/10.20.E2
Encodings:: TeX, pMML, png

10.20.3 $\frac{2}{3}(-\zeta)^{{\frac{3}{2}}}=\int_{1}^{z}\frac{\sqrt{t^{2}-1}}{t}dt=% \sqrt{z^{2}-1}-\mathop{\mathrm{arcsec}\/}\nolimits z,$ $1\leq z<\infty$ ,

Symbols:: : differential of , $\int$ : integral, $\mathop{\mathrm{arcsec}\/}\nolimits z$ : arcsecant function, : complex variable and $\zeta(z)$ : solution
A&S Ref:: 9.3.39
Referenced by:: §10.20(ii), §10.21(viii)
Permalink:: http://dlmf.nist.gov/10.20.E3
Encodings:: TeX, pMML, png

all functions taking their principal values, with $\zeta=\infty,0,-\infty$ , corresponding to $z=0,1,\infty$ , respectively.

As $\nu\to\infty$ through positive real values

10.20.4 $\mathop{J_{{\nu}}\/}\nolimits\!\left(\nu z\right)\sim\left(\frac{4\zeta}{1-z^{% 2}}\right)^{{\frac{1}{4}}}\*\left(\frac{\mathop{\mathrm{Ai}\/}\nolimits\!\left% (\nu^{{\frac{2}{3}}}\zeta\right)}{\nu^{{\frac{1}{3}}}}\sum_{{k=0}}^{\infty}% \frac{A_{k}(\zeta)}{\nu^{{2k}}}+\frac{{\mathop{\mathrm{Ai}\/}\nolimits^{{% \prime}}}\!\left(\nu^{{\frac{2}{3}}}\zeta\right)}{\nu^{{\frac{5}{3}}}}\sum_{{k% =0}}^{\infty}\frac{B_{k}(\zeta)}{\nu^{{2k}}}\right),$

Symbols:: $\mathop{\mathrm{Ai}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{J_{{\nu}}\/}\nolimits\!\left(z\right)$ : Bessel function of the first kind, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable, $\nu$ : complex parameter, $\zeta(z)$ : solution, $A_{k}(\zeta)$ : coefficients and $B_{k}(\zeta)$ : coefficients
A&S Ref:: 9.3.35
Referenced by:: §10.20(ii), §10.20(iii)
Permalink:: http://dlmf.nist.gov/10.20.E4
Encodings:: TeX, pMML, png

10.20.5 $\mathop{Y_{{\nu}}\/}\nolimits\!\left(\nu z\right)\sim-\left(\frac{4\zeta}{1-z^% {2}}\right)^{{\frac{1}{4}}}\left(\frac{\mathop{\mathrm{Bi}\/}\nolimits\!\left(% \nu^{{\frac{2}{3}}}\zeta\right)}{\nu^{{\frac{1}{3}}}}\sum_{{k=0}}^{\infty}% \frac{A_{k}(\zeta)}{\nu^{{2k}}}+\frac{{\mathop{\mathrm{Bi}\/}\nolimits^{{% \prime}}}\!\left(\nu^{{\frac{2}{3}}}\zeta\right)}{\nu^{{\frac{5}{3}}}}\sum_{{k% =0}}^{\infty}\frac{B_{k}(\zeta)}{\nu^{{2k}}}\right),$

Symbols:: $\mathop{\mathrm{Bi}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{Y_{{\nu}}\/}\nolimits\!\left(z\right)$ : Bessel function of the second kind, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable, $\nu$ : complex parameter, $\zeta(z)$ : solution, $A_{k}(\zeta)$ : coefficients and $B_{k}(\zeta)$ : coefficients
A&S Ref:: 9.3.36
Permalink:: http://dlmf.nist.gov/10.20.E5
Encodings:: TeX, pMML, png

10.20.6 $\rselection{\mathop{{H^{{(1)}}_{{\nu}}}\/}\nolimits\!\left(\nu z\right)\\ \mathop{{H^{{(2)}}_{{\nu}}}\/}\nolimits\!\left(\nu z\right)}\sim 2e^{{\mp\pi i% /3}}\left(\frac{4\zeta}{1-z^{2}}\right)^{{\frac{1}{4}}}\left(\frac{\mathop{% \mathrm{Ai}\/}\nolimits\!\left(e^{{\pm 2\pi i/3}}\nu^{{\frac{2}{3}}}\zeta% \right)}{\nu^{{\frac{1}{3}}}}\sum_{{k=0}}^{\infty}\frac{A_{k}(\zeta)}{\nu^{{2k% }}}+\frac{e^{{\pm 2\pi i/3}}{\mathop{\mathrm{Ai}\/}\nolimits^{{\prime}}}\!% \left(e^{{\pm 2\pi i/3}}\nu^{{\frac{2}{3}}}\zeta\right)}{\nu^{{\frac{5}{3}}}}% \sum_{{k=0}}^{\infty}\frac{B_{k}(\zeta)}{\nu^{{2k}}}\right),$

Symbols:: $\mathop{\mathrm{Ai}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{{H^{{(1)}}_{{\nu}}}\/}\nolimits\!\left(z\right)$ : Bessel function of the third kind (or Hankel function), $\mathop{{H^{{(2)}}_{{\nu}}}\/}\nolimits\!\left(z\right)$ : Bessel function of the third kind (or Hankel function), : base of exponential function, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable, $\nu$ : complex parameter, $\zeta(z)$ : solution, $A_{k}(\zeta)$ : coefficients and $B_{k}(\zeta)$ : coefficients
A&S Ref:: 9.3.37
Referenced by:: §10.20(iii), §10.41(v)
Permalink:: http://dlmf.nist.gov/10.20.E6
Encodings:: TeX, pMML, png

10.20.7 ${\mathop{J_{{\nu}}\/}\nolimits^{{\prime}}}\!\left(\nu z\right)\sim-\frac{2}{z}% \left(\frac{1-z^{2}}{4\zeta}\right)^{{\frac{1}{4}}}\*\left(\frac{\mathop{% \mathrm{Ai}\/}\nolimits\!\left(\nu^{{\frac{2}{3}}}\zeta\right)}{\nu^{{\frac{4}% {3}}}}\sum_{{k=0}}^{\infty}\frac{C_{k}(\zeta)}{\nu^{{2k}}}+\frac{{\mathop{% \mathrm{Ai}\/}\nolimits^{{\prime}}}\!\left(\nu^{{\frac{2}{3}}}\zeta\right)}{% \nu^{{\frac{2}{3}}}}\sum_{{k=0}}^{\infty}\frac{D_{k}(\zeta)}{\nu^{{2k}}}\right),$

Symbols:: $\mathop{\mathrm{Ai}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{J_{{\nu}}\/}\nolimits\!\left(z\right)$ : Bessel function of the first kind, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable, $\nu$ : complex parameter, $\zeta(z)$ : solution, $C_{k}(\zeta)$ : coefficients and $D_{k}(\zeta)$ : coefficients
A&S Ref:: 9.3.43
Permalink:: http://dlmf.nist.gov/10.20.E7
Encodings:: TeX, pMML, png

10.20.8 ${\mathop{Y_{{\nu}}\/}\nolimits^{{\prime}}}\!\left(\nu z\right)\sim\frac{2}{z}% \left(\frac{1-z^{2}}{4\zeta}\right)^{{\frac{1}{4}}}\*\left(\frac{\mathop{% \mathrm{Bi}\/}\nolimits\!\left(\nu^{{\frac{2}{3}}}\zeta\right)}{\nu^{{\frac{4}% {3}}}}\sum_{{k=0}}^{\infty}\frac{C_{k}(\zeta)}{\nu^{{2k}}}+\frac{{\mathop{% \mathrm{Bi}\/}\nolimits^{{\prime}}}\!\left(\nu^{{\frac{2}{3}}}\zeta\right)}{% \nu^{{\frac{2}{3}}}}\sum_{{k=0}}^{\infty}\frac{D_{k}(\zeta)}{\nu^{{2k}}}\right),$

Symbols:: $\mathop{\mathrm{Bi}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{Y_{{\nu}}\/}\nolimits\!\left(z\right)$ : Bessel function of the second kind, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable, $\nu$ : complex parameter, $\zeta(z)$ : solution, $C_{k}(\zeta)$ : coefficients and $D_{k}(\zeta)$ : coefficients
A&S Ref:: 9.3.44
Permalink:: http://dlmf.nist.gov/10.20.E8
Encodings:: TeX, pMML, png

10.20.9 $\rselection{{\mathop{{H^{{(1)}}_{{\nu}}}\/}\nolimits^{{\prime}}}\!\left(\nu z% \right)\\ {\mathop{{H^{{(2)}}_{{\nu}}}\/}\nolimits^{{\prime}}}\!\left(\nu z\right)}\sim% \frac{4e^{{\mp 2\pi i/3}}}{z}\left(\frac{1-z^{2}}{4\zeta}\right)^{{\frac{1}{4}% }}\*\left(\frac{e^{{\mp 2\pi i/3}}\mathop{\mathrm{Ai}\/}\nolimits\!\left(e^{{% \pm 2\pi i/3}}\nu^{{\frac{2}{3}}}\zeta\right)}{\nu^{{\frac{4}{3}}}}\sum_{{k=0}% }^{\infty}\frac{C_{k}(\zeta)}{\nu^{{2k}}}+\frac{{\mathop{\mathrm{Ai}\/}% \nolimits^{{\prime}}}\!\left(e^{{\pm 2\pi i/3}}\nu^{{\frac{2}{3}}}\zeta\right)% }{\nu^{{\frac{2}{3}}}}\sum_{{k=0}}^{\infty}\frac{D_{k}(\zeta)}{\nu^{{2k}}}% \right),$

Symbols:: $\mathop{\mathrm{Ai}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{{H^{{(1)}}_{{\nu}}}\/}\nolimits\!\left(z\right)$ : Bessel function of the third kind (or Hankel function), $\mathop{{H^{{(2)}}_{{\nu}}}\/}\nolimits\!\left(z\right)$ : Bessel function of the third kind (or Hankel function), : base of exponential function, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable, $\nu$ : complex parameter, $\zeta(z)$ : solution, $C_{k}(\zeta)$ : coefficients and $D_{k}(\zeta)$ : coefficients
A&S Ref:: 9.3.45
Referenced by:: §10.20(ii)
Permalink:: http://dlmf.nist.gov/10.20.E9
Encodings:: TeX, pMML, png

uniformly for $\in(0,\infty)$ in all cases, where $\mathop{\mathrm{Ai}\/}\nolimits$ and $\mathop{\mathrm{Bi}\/}\nolimits$ are the Airy functions (§9.2).

In the following formulas for the coefficients $A_{k}(\zeta)$ , $B_{k}(\zeta)$ , $C_{k}(\zeta)$ , and $D_{k}(\zeta)$ , $u_{k}$ , $v_{k}$ are the constants defined in §9.7(i), and $U_{k}(p)$ , $V_{k}(p)$ are the polynomials in of degree defined in §10.41(ii).

¶ Interval

10.20.10 $A_{k}(\zeta)=\sum_{{j=0}}^{{2k}}(\tfrac{3}{2})^{j}v_{j}\zeta^{{-3j/2}}U_{{2k-j% }}\left((1-z^{2})^{{-\frac{1}{2}}}\right),$

Symbols:: : nonnegative integer, : complex variable, $\zeta(z)$ : solution, $v_{k}$ : constants, $A_{k}(\zeta)$ : coefficients and $U_{k}(p)$ : polynomials
A&S Ref:: 9.3.40
Referenced by:: ¶ ‣ §10.20(i), §10.41(v), §10.74(i)
Permalink:: http://dlmf.nist.gov/10.20.E10
Encodings:: TeX, pMML, png

10.20.11 $B_{k}(\zeta)=-\zeta^{{-\frac{1}{2}}}\sum_{{j=0}}^{{2k+1}}(\tfrac{3}{2})^{j}u_{% j}\zeta^{{-3j/2}}U_{{2k-j+1}}\left((1-z^{2})^{{-\frac{1}{2}}}\right),$

Symbols:: : nonnegative integer, : complex variable, $\zeta(z)$ : solution, $u_{k}$ : constants, $B_{k}(\zeta)$ : coefficients and $U_{k}(p)$ : polynomials
A&S Ref:: 9.3.40
Referenced by:: §10.21(viii), §10.41(v)
Permalink:: http://dlmf.nist.gov/10.20.E11
Encodings:: TeX, pMML, png

10.20.12 $C_{k}(\zeta)=-\zeta^{{\frac{1}{2}}}\sum_{{j=0}}^{{2k+1}}(\tfrac{3}{2})^{j}v_{j% }\zeta^{{-3j/2}}V_{{2k-j+1}}\left((1-z^{2})^{{-\frac{1}{2}}}\right),$

Symbols:: : nonnegative integer, : complex variable, $\zeta(z)$ : solution, $v_{k}$ : constants, $C_{k}(\zeta)$ : coefficients and $V_{k}(p)$ : polynomials
A&S Ref:: 9.3.46
Referenced by:: §10.21(viii)
Permalink:: http://dlmf.nist.gov/10.20.E12
Encodings:: TeX, pMML, png

10.20.13 $D_{k}(\zeta)=\sum_{{j=0}}^{{2k}}(\tfrac{3}{2})^{j}u_{j}\zeta^{{-3j/2}}V_{{2k-j% }}\left((1-z^{2})^{{-\frac{1}{2}}}\right).$

Symbols:: : nonnegative integer, : complex variable, $\zeta(z)$ : solution, $u_{k}$ : constants, $D_{k}(\zeta)$ : coefficients and $V_{k}(p)$ : polynomials
A&S Ref:: 9.3.46
Referenced by:: ¶ ‣ §10.20(i), §10.74(i)
Permalink:: http://dlmf.nist.gov/10.20.E13
Encodings:: TeX, pMML, png

¶ Interval $1<z<\infty$

In formulas (10.20.10)–(10.20.13) replace $\zeta^{{\frac{1}{2}}}$ , $\zeta^{{-\frac{1}{2}}}$ , $\zeta^{{-3j/2}}$ , and $(1-z^{2})^{{-\frac{1}{2}}}$ by $-i(-\zeta)^{{\frac{1}{2}}}$ , $i(-\zeta)^{{-\frac{1}{2}}}$ , $i^{{3j}}(-\zeta)^{{-3j/2}}$ , and $i(z^{2}-1)^{{-\frac{1}{2}}}$ , respectively.

Note: Another way of arranging the above formulas for the coefficients $A_{k}(\zeta),B_{k}(\zeta),C_{k}(\zeta)$ , and $D_{k}(\zeta)$ would be by analogy with (12.10.42) and (12.10.46). In this way there is less usage of many-valued functions.

¶ Values at $\zeta=0$

10.20.14

$A_{0}(0)=1,$

$A_{1}(0)=-\tfrac{1}{225},$

$A_{2}(0)=\tfrac{1\;51439}{2182\;95000},$

$A_{3}(0)=-\tfrac{8872\;78009}{250\;49351\;25000},\\$

$B_{0}(0)=\tfrac{1}{70}2^{{\frac{1}{3}}},$

$B_{1}(0)=-\tfrac{1213}{10\;23750}2^{{\frac{1}{3}}},$

$B_{2}(0)=\tfrac{1\;65425\;37833}{3774\;32055\;00000}2^{{\frac{1}{3}}},$

$B_{3}(0)=-\tfrac{959\;71711\;84603}{25\;47666\;37125\;00000}2^{{\frac{1}{3}}}.$

Symbols:: $A_{k}(\zeta)$ : coefficients and $B_{k}(\zeta)$ : coefficients
Referenced by:: ¶ ‣ §10.20(i), Equation 10.20.14
Permalink:: http://dlmf.nist.gov/10.20.E14
Encodings:: TeX, TeX, TeX, TeX, TeX, TeX, TeX, TeX, pMML, pMML, pMML, pMML, pMML, pMML, pMML, pMML, png, png, png, png, png, png, png, png
Errata (effective with 1.0.5):: Originally the value given for $B_{3}(0)$ was given incorrectly as $B_{3}(0)=-\tfrac{430\;99056\;39368\;59253}{5\;68167\;34399\;42500\;00000}2^{{% \frac{1}{3}}}$ .
Reported 2012-05-11 by Antony Lee

Each of the coefficients $A_{k}(\zeta)$ , $B_{k}(\zeta)$ , $C_{k}(\zeta)$ , and $D_{k}(\zeta)$ , $k=0,1,2,\ldots$ , is real and infinitely differentiable on the interval $-\infty<\zeta<\infty$ . For (10.20.14) and further information on the coefficients see Temme (1997).

For numerical tables of $\zeta=\zeta(z)$ , $(4\zeta/(1-z^{2}))^{{\frac{1}{4}}}$ and $A_{k}(\zeta)$ , $B_{k}(\zeta)$ , $C_{k}(\zeta)$ , and $D_{k}(\zeta)$ see Olver (1962, pp. 28–42).

§10.20(ii) Complex Variables

Notes:: See Olver (1997b, pp. 419–425) and Olver (1954).
Keywords:: Bessel functions
Referenced by:: ¶ ‣ §10.14, §10.74(i)
Permalink:: http://dlmf.nist.gov/10.20.ii

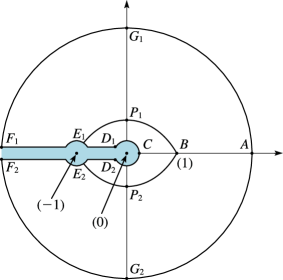
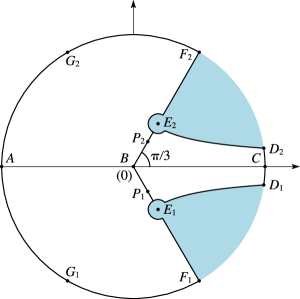
The function $\zeta=\zeta(z)$ given by (10.20.2) and (10.20.3) can be continued analytically to the -plane cut along the negative real axis. Corresponding points of the mapping are shown in Figures 10.20.1 and 10.20.2.

The equations of the curved boundaries $D_{1}E_{1}$ and $D_{2}E_{2}$ in the $\zeta$ -plane are given parametrically by

10.20.15 $\zeta=(\tfrac{3}{2})^{{\frac{2}{3}}}(\tau\mp i\pi)^{{\frac{2}{3}}},$ $0\leq\tau<\infty$ ,

Symbols:: $\zeta(z)$ : solution
Permalink:: http://dlmf.nist.gov/10.20.E15
Encodings:: TeX, pMML, png

respectively.

The curves $BP_{1}E_{1}$ and $BP_{2}E_{2}$ in the -plane are the inverse maps of the line segments

10.20.16 $\zeta=e^{{\mp i\pi/3}}\tau,$ $0\leq\tau\leq(\tfrac{3}{2}\pi)^{{\frac{2}{3}}}$ ,

Symbols:: : base of exponential function and $\zeta(z)$ : solution
Permalink:: http://dlmf.nist.gov/10.20.E16
Encodings:: TeX, pMML, png

respectively. They are given parametrically by

10.20.17 $z=\pm(\tau\mathop{\coth\/}\nolimits\tau-\tau^{2})^{{\frac{1}{2}}}\pm i(\tau^{2% }-\tau\mathop{\tanh\/}\nolimits\tau)^{{\frac{1}{2}}},$ $0\leq\tau\leq\tau_{0}$ ,

Symbols:: $\mathop{\coth\/}\nolimits z$ : hyperbolic cotangent function, $\mathop{\tanh\/}\nolimits z$ : hyperbolic tangent function and : complex variable
Permalink:: http://dlmf.nist.gov/10.20.E17
Encodings:: TeX, pMML, png

where $\tau_{0}=1.19968\ldots$ is the positive root of the equation $\tau=\mathop{\coth\/}\nolimits\tau$ . The points $P_{1},P_{2}$ where these curves intersect the imaginary axis are $\pm ic$ , where

10.20.18 $c=(\tau_{0}^{2}-1)^{{\frac{1}{2}}}=0.66274\ldots.$

Symbols:
Referenced by:: §10.41(iii)
Permalink:: http://dlmf.nist.gov/10.20.E18
Encodings:: TeX, pMML, png

The eye-shaped closed domain in the uncut -plane that is bounded by $BP_{1}E_{1}$ and $BP_{2}E_{2}$ is denoted by $\mathbf{K}$ ; see Figure 10.20.3.

Figure 10.20.1:

-plane. $P_{1}$ and $P_{2}$ are the points $\pm ic$ . $c=0.66274\ldots$ .

Symbols:: : nonnegative integer, : complex variable, : point, : point, $E_{k}$ : points, $F_{k}$ : points, $G_{k}$ : points, $P_{k}$ : points, $D_{k}(\zeta)$ : coefficients, and : point
Referenced by:: §10.20(ii)
Permalink:: http://dlmf.nist.gov/10.20.F1
Encodings:: pdf, png

Figure 10.20.2: $\zeta$ -plane. $E_{1}$ and $E_{2}$ are the points $e^{{\mp\pi i/3}}(3\pi/2)^{{2/3}}.$

Symbols:: : base of exponential function, $\zeta(z)$ : solution and $E_{k}$ : points
Referenced by:: §10.20(ii)
Permalink:: http://dlmf.nist.gov/10.20.F2
Encodings:: pdf, png

Figure 10.20.3:

-plane. Domain $\mathbf{K}$ (unshaded). $c=0.66274\dots$ .

Symbols:: : complex variable, $\mathbf{K}$ : domain and
Referenced by:: §10.20(ii), ¶ ‣ §10.21(ix), §10.41(iii)
Permalink:: http://dlmf.nist.gov/10.20.F3
Encodings:: pdf, png

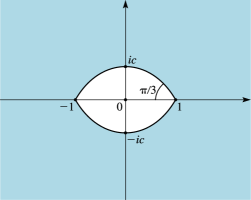
As $\nu\to\infty$ through positive real values the expansions (10.20.4)–(10.20.9) apply uniformly for $|\mathop{\mathrm{ph}\/}\nolimits z|\leq\pi-\delta$ , the coefficients $A_{k}(\zeta)$ , $B_{k}(\zeta)$ , $C_{k}(\zeta)$ , and $D_{k}(\zeta)$ , being the analytic continuations of the functions defined in §10.20(i) when $\zeta$ is real.

For proofs of the above results and for error bounds and extensions of the regions of validity see Olver (1997b, pp. 419–425). For extensions to complex $\nu$ see Olver (1954). For resurgence properties of the coefficients (§2.7(ii)) see Howls and Olde Daalhuis (1999). For further results see Dunster (2001a), Wang and Wong (2002), and Paris (2004).

§10.20(iii) Double Asymptotic Properties

Keywords:: Bessel functions, Hankel functions
Permalink:: http://dlmf.nist.gov/10.20.iii

For asymptotic properties of the expansions (10.20.4)–(10.20.6) with respect to large values of see §10.41(v).

© 2010–2013 NIST / Privacy Policy / Disclaimer / Feedback; Version 1.0.6; Release date 2013-05-06 Math-Image version (See MathML) . A Printed Companionis available. 10.19 Asymptotic Expansions for Large Order 10.21 Zeros

§10.20 Uniform Asymptotic Expansions for Large Order

Contents

§10.20(i) Real Variables

¶ Interval

¶ Interval

¶ Values at

§10.20(ii) Complex Variables

§10.20(iii) Double Asymptotic Properties

¶ Interval $1<z<\infty$

¶ Values at $\zeta=0$