§1.6 Vectors and Vector-Valued Functions

Keywords:: vectors, vector-valued functions
Referenced by:: §1.1
Permalink:: http://dlmf.nist.gov/1.6

§1.6(i) Vectors
§1.6(ii) Vectors: Alternative Notations
§1.6(iii) Vector-Valued Functions
§1.6(iv) Path and Line Integrals
§1.6(v) Surfaces and Integrals over Surfaces

§1.6(i) Vectors

Notes:: See Marsden and Tromba (1996, Chapter 1). For (1.6.9) see Hubbard and Hubbard (2002, pp. 82–84).
Permalink:: http://dlmf.nist.gov/1.6.i

1.6.1

$\mathbf{a}=(a_{1},a_{2},a_{3}),$

$\mathbf{b}=(b_{1},b_{2},b_{3}).$

Permalink:: http://dlmf.nist.gov/1.6.E1
Encodings:: TeX, TeX, pMML, pMML, png, png

¶ Dot Product (or Scalar Product)

Keywords:: vectors

1.6.2 $\mathbf{a}\cdot\mathbf{b}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}.$

Permalink:: http://dlmf.nist.gov/1.6.E2
Encodings:: TeX, pMML, png

¶ Magnitude and Angle of Vector $\mathbf{a}$

Keywords:: vectors

1.6.3 $\|\mathbf{a}\|=\sqrt{\mathbf{a}\cdot\mathbf{a}},$

Permalink:: http://dlmf.nist.gov/1.6.E3
Encodings:: TeX, pMML, png

1.6.4 $\mathop{\cos\/}\nolimits\theta=\frac{\mathbf{a}\cdot\mathbf{b}}{\|\mathbf{a}\|\;\|\mathbf{b}\|};$

Symbols:: $\mathop{\cos\/}\nolimits z$ : cosine function and $\theta$ : angle between $\mathbf{a}$ and $\mathbf{b}$
Permalink:: http://dlmf.nist.gov/1.6.E4
Encodings:: TeX, pMML, png

$\theta$ is the angle between $\mathbf{a}$ and $\mathbf{b}$ .

¶ Unit Vectors

Keywords:: vectors

1.6.5

$\mathbf{i}=(1,0,0),$

$\mathbf{j}=(0,1,0),$

$\mathbf{k}=(0,0,1),$

Symbols:: $\mathbf{i}$ : unit vector, $\mathbf{j}$ : unit vector and $\mathbf{k}$ : unit vector
Referenced by:: ¶ ‣ §1.6(ii)
Permalink:: http://dlmf.nist.gov/1.6.E5
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

1.6.6 $\mathbf{a}=a_{1}\mathbf{i}+a_{2}\mathbf{j}+a_{3}\mathbf{k}.$

Symbols:: $\mathbf{i}$ : unit vector, $\mathbf{j}$ : unit vector and $\mathbf{k}$ : unit vector
Permalink:: http://dlmf.nist.gov/1.6.E6
Encodings:: TeX, pMML, png

¶ Cross Product (or Vector Product)

Keywords:: parallelepiped, parallelogram, vectors

1.6.7

$\mathbf{i}\times\mathbf{j}=\mathbf{k},$

$\mathbf{j}\times\mathbf{k}=\mathbf{i},$

$\mathbf{k}\times\mathbf{i}=\mathbf{j},$

Symbols:: $\mathbf{i}$ : unit vector, $\mathbf{j}$ : unit vector and $\mathbf{k}$ : unit vector
Referenced by:: ¶ ‣ §1.6(ii)
Permalink:: http://dlmf.nist.gov/1.6.E7
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

1.6.8

$\mathbf{j}\times\mathbf{i}=-\mathbf{k},$

$\mathbf{k}\times\mathbf{j}=-\mathbf{i},$

$\mathbf{i}\times\mathbf{k}=-\mathbf{j}.$

Symbols:: $\mathbf{i}$ : unit vector, $\mathbf{j}$ : unit vector and $\mathbf{k}$ : unit vector
Referenced by:: ¶ ‣ §1.6(ii)
Permalink:: http://dlmf.nist.gov/1.6.E8
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

1.6.9 $\mathbf{a}\times\mathbf{b}=\begin{vmatrix}\mathbf{i}&\mathbf{j}&\mathbf{k}\\ a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\end{vmatrix}\\ =(a_{2}b_{3}-a_{3}b_{2})\mathbf{i}+(a_{3}b_{1}-a_{1}b_{3})\mathbf{j}+(a_{1}b_{2}-a_{2}b_{1})\mathbf{k}\\ =\|\mathbf{a}\|\|\mathbf{b}\|(\mathop{\sin\/}\nolimits\theta)\mathbf{n},$

Symbols:: $\mathop{\sin\/}\nolimits z$ : sine function, $\theta$ : angle between $\mathbf{a}$ and $\mathbf{b}$ , $\mathbf{i}$ : unit vector, $\mathbf{j}$ : unit vector and $\mathbf{k}$ : unit vector
Referenced by:: §1.6(i)
Permalink:: http://dlmf.nist.gov/1.6.E9
Encodings:: TeX, pMML, png

where $\mathbf{n}$ is the unit vector normal to $\mathbf{a}$ and $\mathbf{b}$ whose direction is determined by the right-hand rule; see Figure 1.6.1.

Figure 1.6.1: Vector notation. Right-hand rule for cross products.

Referenced by:: ¶ ‣ §1.6(i)
Permalink:: http://dlmf.nist.gov/1.6.F1
Encodings:: pdf, png

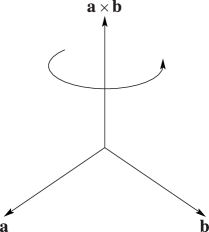
Area of parallelogram with vectors $\mathbf{a}$ and $\mathbf{b}$ as sides $=\|\mathbf{a}\times\mathbf{b}\|$ .

Volume of a parallelepiped with vectors $\mathbf{a}$ , $\mathbf{b}$ , and $\mathbf{c}$ as edges $=\left|\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c})\right|$ .

1.6.10 $\mathbf{a}\times(\mathbf{b}\times\mathbf{c})=\mathbf{b}(\mathbf{a}\cdot\mathbf{c})-\mathbf{c}(\mathbf{a}\cdot\mathbf{b}),$

Permalink:: http://dlmf.nist.gov/1.6.E10
Encodings:: TeX, pMML, png

1.6.11 $(\mathbf{a}\times\mathbf{b})\times\mathbf{c}=\mathbf{b}(\mathbf{a}\cdot\mathbf{c})-\mathbf{a}(\mathbf{b}\cdot\mathbf{c}).$

Permalink:: http://dlmf.nist.gov/1.6.E11
Encodings:: TeX, pMML, png

§1.6(ii) Vectors: Alternative Notations

Keywords:: vectors
Permalink:: http://dlmf.nist.gov/1.6.ii

The following notations are often used in the physics literature; see for example Lorentz et al. (1923, pp. 122–123).

¶ Einstein Summation Convention

Keywords:: Einstein summation convention for vectors, vectors

Much vector algebra involves summation over suffices of products of vector components. In almost all cases of repeated suffices, we can suppress the summation notation entirely, if it is understood that an implicit sum is to be taken over any repeated suffix. Thus pairs of indefinite suffices in an expression are resolved by being summed over (or “traced” over).

¶ Example

1.6.12 $a_{j}b_{j}=\sum _{{j=1}}^{3}a_{j}b_{j}=\mathbf{a}\cdot\mathbf{b}.$

Symbols:: $j$ : integer
Permalink:: http://dlmf.nist.gov/1.6.E12
Encodings:: TeX, pMML, png

Next,

1.6.13

$\boldsymbol{{e_{{1}}}}=(1,0,0),$

$\boldsymbol{{e_{{2}}}}=(0,1,0),$

$\boldsymbol{{e_{{3}}}}=(0,0,1);$

Symbols:: $\boldsymbol{{e_{j}}}$ : unit vectors
Permalink:: http://dlmf.nist.gov/1.6.E13
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

compare (1.6.5). Thus $a_{j}\boldsymbol{{e_{{j}}}}=\mathbf{a}$ .

¶ Levi-Civita Symbol

Keywords:: Levi-Civita symbol for vectors, vectors

1.6.14 $\epsilon _{{j,k,\ell}}=\begin{cases}+1,&\text{if }j,k,\ell\text{ is even permutation of }1,2,3,\\ -1,&\text{if }j,k,\ell\text{ is odd permutation of }1,2,3,\\ 0,&\text{otherwise}.\end{cases}$

Defines:: $\epsilon _{{j,k,\ell}}$ : Levi-Civita symbol
Symbols:: $j$ : integer and $k$ : integer
Permalink:: http://dlmf.nist.gov/1.6.E14
Encodings:: TeX, pMML, png

¶ Examples

Keywords:: Einstein summation convention for vectors, parallelepiped, vectors

1.6.15

$\epsilon _{{1,2,3}}=\epsilon _{{3,1,2}}=1,$

$\epsilon _{{2,1,3}}=\epsilon _{{3,2,1}}=-1,$

$\epsilon _{{2,2,1}}=0.$

Symbols:: $\epsilon _{{j,k,\ell}}$ : Levi-Civita symbol
Permalink:: http://dlmf.nist.gov/1.6.E15
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

1.6.16 $\epsilon _{{j,k,\ell}}\epsilon _{{\ell,m,n}}=\delta _{{j,m}}\delta _{{k,n}}-\delta _{{j,n}}\delta _{{k,m}},$

Symbols:: $\delta _{{j,k}}$ : Kronecker delta, $\epsilon _{{j,k,\ell}}$ : Levi-Civita symbol, $j$ : integer, $k$ : integer, $m$ : nonnegative integer and $n$ : nonnegative integer
Permalink:: http://dlmf.nist.gov/1.6.E16
Encodings:: TeX, pMML, png

where $\delta _{{j,k}}$ is the Kronecker delta.

1.6.17 $\boldsymbol{{e_{{j}}}}\times\boldsymbol{{e_{{k}}}}=\epsilon _{{j,k,\ell}}\boldsymbol{{e_{{\ell}}}};$

Symbols:: $\epsilon _{{j,k,\ell}}$ : Levi-Civita symbol, $j$ : integer, $k$ : integer and $\boldsymbol{{e_{j}}}$ : unit vectors
Permalink:: http://dlmf.nist.gov/1.6.E17
Encodings:: TeX, pMML, png

compare (1.6.8).

1.6.18 $a_{j}\boldsymbol{{e_{{j}}}}\times b_{k}\boldsymbol{{e_{{k}}}}=\epsilon _{{j,k,\ell}}a_{j}b_{k}\boldsymbol{{e_{{\ell}}}};$

Symbols:: $\epsilon _{{j,k,\ell}}$ : Levi-Civita symbol, $j$ : integer, $k$ : integer and $\boldsymbol{{e_{j}}}$ : unit vectors
Permalink:: http://dlmf.nist.gov/1.6.E18
Encodings:: TeX, pMML, png

compare (1.6.7)–(1.6.8).

Lastly, the volume of a parallelepiped with vectors $\mathbf{a}$ , $\mathbf{b}$ , and $\mathbf{c}$ as edges is $|\epsilon _{{j,k,\ell}}a_{j}b_{k}c_{\ell}|$ .

§1.6(iii) Vector-Valued Functions

Notes:: See Marsden and Tromba (1996, pp. 144–147, 273–283).
Keywords:: functions
Permalink:: http://dlmf.nist.gov/1.6.iii

¶ Del Operator

Keywords:: del operator, vector-valued functions

1.6.19 $\nabla=\mathbf{i}\frac{\partial}{\partial x}+\mathbf{j}\frac{\partial}{\partial y}+\mathbf{k}\frac{\partial}{\partial z}.$

Symbols:: $\frac{\partial f}{\partial x}$ : partial derivative of $f$ with respect to $x$ , $z$ : variable, $\mathbf{i}$ : unit vector, $\mathbf{j}$ : unit vector and $\mathbf{k}$ : unit vector
Permalink:: http://dlmf.nist.gov/1.6.E19
Encodings:: TeX, pMML, png

The gradient of a differentiable scalar function $f(x,y,z)$ is

1.6.20 $\gradient f=\nabla f=\frac{\partial f}{\partial x}\mathbf{i}+\frac{\partial f}{\partial y}\mathbf{j}+\frac{\partial f}{\partial z}\mathbf{k}.$

Defines:: $\gradient$ : gradient of differentiable scalar function
Symbols:: $\frac{\partial f}{\partial x}$ : partial derivative of $f$ with respect to $x$ , $z$ : variable, $\mathbf{i}$ : unit vector, $\mathbf{j}$ : unit vector and $\mathbf{k}$ : unit vector
Permalink:: http://dlmf.nist.gov/1.6.E20
Encodings:: TeX, pMML, png

The divergence of a differentiable vector-valued function $\mathbf{F}=F_{1}\mathbf{i}+F_{2}\mathbf{j}+F_{3}\mathbf{k}$ is

1.6.21 $\divergence\mathbf{F}=\nabla\cdot\mathbf{F}=\frac{\partial F_{1}}{\partial x}+\frac{\partial F_{2}}{\partial y}+\frac{\partial F_{3}}{\partial z}.$

Defines:: $\divergence$ : divergence of vector-valued function
Symbols:: $\frac{\partial f}{\partial x}$ : partial derivative of $f$ with respect to $x$ , $z$ : variable and $F_{j}$ : vector function components
Permalink:: http://dlmf.nist.gov/1.6.E21
Encodings:: TeX, pMML, png

The curl of $\mathbf{F}$ is

1.6.22 $\curl\mathbf{F}=\nabla\times\mathbf{F}=\begin{vmatrix}\mathbf{i}&\mathbf{j}&\mathbf{k}\\ \displaystyle{\frac{\partial}{\partial x}}&\displaystyle{\frac{\partial}{\partial y}}&\displaystyle{\frac{\partial}{\partial z}}\\ F_{1}&F_{2}&F_{3}\end{vmatrix}\\ =\left(\frac{\partial F_{3}}{\partial y}-\frac{\partial F_{2}}{\partial z}\right)\mathbf{i}+\left(\frac{\partial F_{1}}{\partial z}-\frac{\partial F_{3}}{\partial x}\right)\mathbf{j}+\left(\frac{\partial F_{2}}{\partial x}-\frac{\partial F_{1}}{\partial y}\right)\mathbf{k}.$

Defines:: $\curl$ : of vector-valued function
Symbols:: $\frac{\partial f}{\partial x}$ : partial derivative of $f$ with respect to $x$ , $z$ : variable, $\mathbf{i}$ : unit vector, $\mathbf{j}$ : unit vector, $\mathbf{k}$ : unit vector and $F_{j}$ : vector function components
Permalink:: http://dlmf.nist.gov/1.6.E22
Encodings:: TeX, pMML, png

1.6.23 $\nabla(fg)=f\nabla g+g\nabla f,$

Permalink:: http://dlmf.nist.gov/1.6.E23
Encodings:: TeX, pMML, png

1.6.24 $\nabla(f/g)=(g\nabla f-f\nabla g)/g^{2},$

Permalink:: http://dlmf.nist.gov/1.6.E24
Encodings:: TeX, pMML, png

1.6.25 $\nabla\cdot(f\mathbf{F})=f(\nabla\cdot\mathbf{F})+\mathbf{F}\cdot\nabla f,$

Permalink:: http://dlmf.nist.gov/1.6.E25
Encodings:: TeX, pMML, png

1.6.26 $\nabla\cdot(\mathbf{F}\times\mathbf{G})=\mathbf{G}\cdot(\nabla\times\mathbf{F})-\mathbf{F}\cdot(\nabla\times\mathbf{G}),$

Permalink:: http://dlmf.nist.gov/1.6.E26
Encodings:: TeX, pMML, png

1.6.27 $\nabla\cdot(\nabla\times\mathbf{F})=\divergence\curl\mathbf{F}=0,$

Symbols:: $\curl$ : of vector-valued function and $\divergence$ : divergence of vector-valued function
Permalink:: http://dlmf.nist.gov/1.6.E27
Encodings:: TeX, pMML, png

1.6.28 $\nabla\times(f\mathbf{F})=f(\nabla\times\mathbf{F})+(\nabla f)\times\mathbf{F},$

Permalink:: http://dlmf.nist.gov/1.6.E28
Encodings:: TeX, pMML, png

1.6.29 $\nabla\times(\nabla f)=\curl\gradient f=0,$

Symbols:: $\curl$ : of vector-valued function and $\gradient$ : gradient of differentiable scalar function
Permalink:: http://dlmf.nist.gov/1.6.E29
Encodings:: TeX, pMML, png

1.6.30 $\nabla^{2}f=\nabla\cdot(\nabla f),$

Permalink:: http://dlmf.nist.gov/1.6.E30
Encodings:: TeX, pMML, png

1.6.31 $\nabla^{2}(fg)=f\nabla^{2}g+g\nabla^{2}f+2(\nabla f\cdot\nabla g),$

Permalink:: http://dlmf.nist.gov/1.6.E31
Encodings:: TeX, pMML, png

1.6.32 $\nabla\cdot(\nabla f\times\nabla g)=0,$

Permalink:: http://dlmf.nist.gov/1.6.E32
Encodings:: TeX, pMML, png

1.6.33 $\nabla\cdot(f\nabla g-g\nabla f)=f\nabla^{2}g-g\nabla^{2}f,$

Permalink:: http://dlmf.nist.gov/1.6.E33
Encodings:: TeX, pMML, png

1.6.34 $\nabla\times(\nabla\times\mathbf{F})=\curl\curl\mathbf{F}=\nabla(\nabla\cdot\mathbf{F})-\nabla^{2}\mathbf{F}.$

Symbols:: $\curl$ : of vector-valued function
Permalink:: http://dlmf.nist.gov/1.6.E34
Encodings:: TeX, pMML, png

§1.6(iv) Path and Line Integrals

Notes:: See Marsden and Tromba (1996, pp. 396–417, 470).
Keywords:: boundary points, closed point set, curve, integrals, open point set, path, piecewise differentiable curve, simple closed curve, vector-valued functions
Permalink:: http://dlmf.nist.gov/1.6.iv

Note: The terminology open and closed sets and boundary points in the $(x,y)$ plane that is used in this subsection and §1.6(v) is analogous to that introduced for the complex plane in §1.9(ii).

$\mathbf{c}(t)=(x(t),y(t),z(t))$ , with $t$ ranging over an interval and $x(t),y(t),z(t)$ differentiable, defines a path.

1.6.35 $\mathbf{c}^{{\prime}}(t)=(x^{{\prime}}(t),y^{{\prime}}(t),z^{{\prime}}(t)).$

Permalink:: http://dlmf.nist.gov/1.6.E35
Encodings:: TeX, pMML, png

The length of a path for $a\leq t\leq b$ is

1.6.36 $\int _{a}^{b}\|\mathbf{c}^{{\prime}}(t)\| dt.$

Symbols:: $dx$ : differential of $x$ and $\int$ : integral
Permalink:: http://dlmf.nist.gov/1.6.E36
Encodings:: TeX, pMML, png

The path integral of a continuous function $f(x,y,z)$ is

1.6.37 $\int _{{\mathbf{c}}}fds=\int^{b}_{a}f(x(t),y(t),z(t))\|\mathbf{c}^{{\prime}}(t)\| dt.$

Symbols:: $dx$ : differential of $x$ and $\int$ : integral
Permalink:: http://dlmf.nist.gov/1.6.E37
Encodings:: TeX, pMML, png

The line integral of a vector-valued function $\mathbf{F}=F_{1}\mathbf{i}+F_{2}\mathbf{j}+F_{3}\mathbf{k}$ along $\mathbf{c}$ is given by

1.6.38 $\int _{{\mathbf{c}}}\mathbf{F}\cdot d\mathbf{s}=\int^{b}_{a}\mathbf{F}(\mathbf{c}(t))\cdot\mathbf{c}^{{\prime}}(t)dt=\int^{b}_{a}\left(F_{1}\frac{dx}{dt}+F_{2}\frac{dy}{dt}+F_{3}\frac{dz}{dt}\right)dt=\int _{{\mathbf{c}}}F_{1}dx+F_{2}dy+F_{3}dz.$

Symbols:: $\frac{df}{dx}$ : derivative of $f$ with respect to $x$ , $dx$ : differential of $x$ , $\int$ : integral and $F_{j}$ : vector function components
Permalink:: http://dlmf.nist.gov/1.6.E38
Encodings:: TeX, pMML, png

A path $\mathbf{c}_{1}(t)$ , $t\in[a,b]$ , is a reparametrization of $\mathbf{c}(t^{{\prime}})$ , $t^{{\prime}}\in[a^{{\prime}},b^{{\prime}}]$ , if $\mathbf{c}_{1}(t)=\mathbf{c}(t^{{\prime}})$ and $t^{{\prime}}=h(t)$ with $h(t)$ differentiable and monotonic. If $h(a)=a^{{\prime}}$ and $h(b)=b^{{\prime}}$ , then the reparametrization is called orientation-preserving, and

1.6.39 $\int _{{\mathbf{c}}}\mathbf{F}\cdot d\mathbf{s}=\int _{{\mathbf{c}_{1}}}\mathbf{F}\cdot d\mathbf{s}.$

Symbols:: $dx$ : differential of $x$ and $\int$ : integral
Permalink:: http://dlmf.nist.gov/1.6.E39
Encodings:: TeX, pMML, png

If $h(a)=b^{{\prime}}$ and $h(b)=a^{{\prime}}$ , then the reparametrization is orientation-reversing and

1.6.40 $\int _{{\mathbf{c}}}\mathbf{F}\cdot d\mathbf{s}=-\int _{{\mathbf{c}_{1}}}\mathbf{F}\cdot d\mathbf{s}.$

Symbols:: $dx$ : differential of $x$ and $\int$ : integral
Permalink:: http://dlmf.nist.gov/1.6.E40
Encodings:: TeX, pMML, png

In either case

1.6.41 $\int _{{\mathbf{c}}}fds=\int _{{\mathbf{c}_{1}}}fds,$

Symbols:: $dx$ : differential of $x$ and $\int$ : integral
Permalink:: http://dlmf.nist.gov/1.6.E41
Encodings:: TeX, pMML, png

when $f$ is continuous, and

1.6.42 $\int _{{\mathbf{c}}}\nabla f\cdot d\mathbf{s}=f(\mathbf{c}(b))-f(\mathbf{c}(a)),$

Symbols:: $dx$ : differential of $x$ and $\int$ : integral
Permalink:: http://dlmf.nist.gov/1.6.E42
Encodings:: TeX, pMML, png

when $f$ is continuously differentiable.

The geometrical image $C$ of a path $\mathbf{c}$ is called a simple closed curve if $\mathbf{c}$ is one-to-one, with the exception $\mathbf{c}(a)=\mathbf{c}(b)$ . The curve $C$ is piecewise differentiable if $\mathbf{c}$ is piecewise differentiable. Note that $C$ can be given an orientation by means of $\mathbf{c}$ .

¶ Green’s Theorem

Keywords:: Green’s theorem for vector-valued functions, functions, vector-valued functions

Let

1.6.43 $\mathbf{F}(x,y)=F_{1}(x,y)\mathbf{i}+F_{2}(x,y)\mathbf{j}$

Symbols:: $(a,b)$ : open interval, $\mathbf{i}$ : unit vector, $\mathbf{j}$ : unit vector and $F_{j}$ : vector function components
Permalink:: http://dlmf.nist.gov/1.6.E43
Encodings:: TeX, pMML, png

and $S$ be the closed and bounded point set in the $(x,y)$ plane having a simple closed curve $C$ as boundary. If $C$ is oriented in the positive (anticlockwise) sense, then

1.6.44 $\iint _{S}\left(\frac{\partial F_{2}}{\partial x}-\frac{\partial F_{1}}{\partial y}\right)dA=\int _{C}\mathbf{F}\cdot d\mathbf{s}=\int _{C}F_{1}dx+F_{2}dy.$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral, $\frac{\partial f}{\partial x}$ : partial derivative of $f$ with respect to $x$ , $S$ : closed region, $C$ : closed curve and $F_{j}$ : vector function components
Referenced by:: ¶ ‣ §1.6(iv)
Permalink:: http://dlmf.nist.gov/1.6.E44
Encodings:: TeX, pMML, png

Sufficient conditions for this result to hold are that $F_{1}(x,y)$ and $F_{2}(x,y)$ are continuously differentiable on $S$ , and $C$ is piecewise differentiable.

The area of $S$ can be found from (1.6.44) by taking $\mathbf{F}(x,y)=-y\mathbf{i}$ , $x\mathbf{j}$ , or $-\frac{1}{2}y\mathbf{i}+\frac{1}{2}x\mathbf{j}$ .

§1.6(v) Surfaces and Integrals over Surfaces

Notes:: See Marsden and Tromba (1996, pp. 421–459, 485, 506).
Keywords:: integrals, parametrized surfaces, surface
Referenced by:: §1.6(iv)
Permalink:: http://dlmf.nist.gov/1.6.v

A parametrized surface $S$ is defined by

1.6.45 $\boldsymbol{{\Phi}}(u,v)=(x(u,v),y(u,v),z(u,v))$

Symbols:: $(a,b)$ : open interval and $\boldsymbol{{\Phi}}(x,y,z)$ : parameterization
Permalink:: http://dlmf.nist.gov/1.6.E45
Encodings:: TeX, pMML, png

with $(u,v)\in D$ , an open set in the plane.

For $x$ , $y$ , and $z$ continuously differentiable, the vectors

1.6.46 $\mathbf{T}_{u}=\frac{\partial x}{\partial u}(u_{0},v_{0})\mathbf{i}+\frac{\partial y}{\partial u}(u_{0},v_{0})\mathbf{j}+\frac{\partial z}{\partial u}(u_{0},v_{0})\mathbf{k}$

Symbols:: $(a,b)$ : open interval, $\frac{\partial f}{\partial x}$ : partial derivative of $f$ with respect to $x$ , $\mathbf{i}$ : unit vector, $\mathbf{j}$ : unit vector and $\mathbf{k}$ : unit vector
Permalink:: http://dlmf.nist.gov/1.6.E46
Encodings:: TeX, pMML, png

and

1.6.47 $\mathbf{T}_{v}=\frac{\partial x}{\partial v}(u_{0},v_{0})\mathbf{i}+\frac{\partial y}{\partial v}(u_{0},v_{0})\mathbf{j}+\frac{\partial z}{\partial v}(u_{0},v_{0})\mathbf{k}$

Symbols:: $(a,b)$ : open interval, $\frac{\partial f}{\partial x}$ : partial derivative of $f$ with respect to $x$ , $\mathbf{i}$ : unit vector, $\mathbf{j}$ : unit vector and $\mathbf{k}$ : unit vector
Permalink:: http://dlmf.nist.gov/1.6.E47
Encodings:: TeX, pMML, png

are tangent to the surface at $\boldsymbol{{\Phi}}(u_{0},v_{0})$ . The surface is smooth at this point if $\mathbf{T}_{u}\times\mathbf{T}_{v}\not=0$ . A surface is smooth if it is smooth at every point. The vector $\mathbf{T}_{u}\times\mathbf{T}_{v}$ at $(u_{0},v_{0})$ is normal to the surface at $\boldsymbol{{\Phi}}(u_{0},v_{0})$ .

The area $A(S)$ of a parametrized smooth surface is given by

1.6.48 $A(S)=\iint _{D}\|\mathbf{T}_{u}\times\mathbf{T}_{v}\| dudv,$

Symbols:: $dx$ : differential of $x$ , $S$ : parameterized surface, $D$ : open set in the plane and $A(S)$ : area of a parameterized smooth surface $S$
Permalink:: http://dlmf.nist.gov/1.6.E48
Encodings:: TeX, pMML, png

and

1.6.49 $\|\mathbf{T}_{u}\times\mathbf{T}_{v}\|=\sqrt{\left(\frac{\partial(x,y)}{\partial(u,v)}\right)^{2}+\left(\frac{\partial(y,z)}{\partial(u,v)}\right)^{2}+\left(\frac{\partial(x,z)}{\partial(u,v)}\right)^{2}}.$

Symbols:: $(a,b)$ : open interval and $\frac{\partial f}{\partial x}$ : partial derivative of $f$ with respect to $x$
Permalink:: http://dlmf.nist.gov/1.6.E49
Encodings:: TeX, pMML, png

The area is independent of the parametrizations.

For a sphere $x=\rho\mathop{\sin\/}\nolimits\theta\mathop{\cos\/}\nolimits\phi$ , $y=\rho\mathop{\sin\/}\nolimits\theta\mathop{\sin\/}\nolimits\phi$ , $z=\rho\mathop{\cos\/}\nolimits\theta$ ,

1.6.50 $\|\mathbf{T}_{{\theta}}\times\mathbf{T}_{{\phi}}\|=\rho^{2}\left|\mathop{\sin\/}\nolimits\theta\right|.$

Symbols:: $\mathop{\sin\/}\nolimits z$ : sine function, $\rho$ : radius, $\theta$ : angle and $\phi$ : angle
Permalink:: http://dlmf.nist.gov/1.6.E50
Encodings:: TeX, pMML, png

For a surface $z=f(x,y)$ ,

1.6.51 $A(S)=\iint _{D}\sqrt{1+\left(\frac{\partial f}{\partial x}\right)^{2}+\left(\frac{\partial f}{\partial y}\right)^{2}}dA.$

Symbols:: $dx$ : differential of $x$ , $\frac{\partial f}{\partial x}$ : partial derivative of $f$ with respect to $x$ , $S$ : parameterized surface, $D$ : open set in the plane and $A(S)$ : area of a parameterized smooth surface $S$
Permalink:: http://dlmf.nist.gov/1.6.E51
Encodings:: TeX, pMML, png

For a surface of revolution, $y=f(x)$ , $x\in[a,b]$ , about the $x$ -axis,

1.6.52 $A(S)=2\pi\int^{b}_{a}|f(x)|\sqrt{1+(f^{{\prime}}(x))^{2}}dx,$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral, $S$ : parameterized surface and $A(S)$ : area of a parameterized smooth surface $S$
Permalink:: http://dlmf.nist.gov/1.6.E52
Encodings:: TeX, pMML, png

and about the $y$ -axis,

1.6.53 $A(S)=2\pi\int^{b}_{a}|x|\sqrt{1+(f^{{\prime}}(x))^{2}}dx.$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral, $S$ : parameterized surface and $A(S)$ : area of a parameterized smooth surface $S$
Permalink:: http://dlmf.nist.gov/1.6.E53
Encodings:: TeX, pMML, png

The integral of a continuous function $f(x,y,z)$ over a surface $S$ is

1.6.54 $\iint _{S}f(x,y,z)dS=\iint _{D}f(\boldsymbol{{\Phi}}(u,v))\|\mathbf{T}_{u}\times\mathbf{T}_{v}\| dudv.$

Symbols:: $dx$ : differential of $x$ , $S$ : parameterized surface, $\boldsymbol{{\Phi}}(x,y,z)$ : parameterization and $D$ : open set in the plane
Permalink:: http://dlmf.nist.gov/1.6.E54
Encodings:: TeX, pMML, png

For a vector-valued function $\mathbf{F}$ ,

1.6.55 $\iint _{S}\mathbf{F}\cdot d\mathbf{S}=\iint _{D}\mathbf{F}\cdot(\mathbf{T}_{u}\times\mathbf{T}_{v})dudv,$

Symbols:: $dx$ : differential of $x$ , $S$ : parameterized surface and $D$ : open set in the plane
Permalink:: http://dlmf.nist.gov/1.6.E55
Encodings:: TeX, pMML, png

where $d\mathbf{S}$ is the surface element with an attached normal direction $\mathbf{T}_{u}\times\mathbf{T}_{v}$ .

A surface is orientable if a continuously varying normal can be defined at all points of the surface. An orientable surface is oriented if suitable normals have been chosen. A parametrization $\boldsymbol{{\Phi}}(u,v)$ of an oriented surface $S$ is orientation preserving if $\mathbf{T}_{u}\times\mathbf{T}_{v}$ has the same direction as the chosen normal at each point of $S$ , otherwise it is orientation reversing.

If $\boldsymbol{{\Phi}}_{1}$ and $\boldsymbol{{\Phi}}_{2}$ are both orientation preserving or both orientation reversing parametrizations of $S$ defined on open sets $D_{1}$ and $D_{2}$ respectively, then

1.6.56 $\iint _{{\boldsymbol{{\Phi}}_{1}(D_{1})}}\mathbf{F}\cdot d\mathbf{S}=\iint _{{\boldsymbol{{\Phi}}_{2}(D_{2})}}\mathbf{F}\cdot d\mathbf{S};$

Symbols:: $dx$ : differential of $x$ , $\boldsymbol{{\Phi}}(x,y,z)$ : parameterization and $D$ : open set in the plane
Permalink:: http://dlmf.nist.gov/1.6.E56
Encodings:: TeX, pMML, png

otherwise, one is the negative of the other.

¶ Stokes’s Theorem

Keywords:: Stokes’ theorem for vector-valued functions, vector-valued functions

Suppose $S$ is an oriented surface with boundary $\partial S$ which is oriented so that its direction is clockwise relative to the normals of $S$ . Then

1.6.57 $\iint _{S}(\nabla\times\mathbf{F})\cdot d\mathbf{S}=\int _{{\partial S}}\mathbf{F}\cdot d\mathbf{s},$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral, $\partial x$ : partial differential of $x$ and $S$ : parameterized surface
Permalink:: http://dlmf.nist.gov/1.6.E57
Encodings:: TeX, pMML, png

when $\mathbf{F}$ is a continuously differentiable vector-valued function.

¶ Gauss’s (or Divergence) Theorem

Keywords:: Gauss’s theorem for vector-valued functions, divergence theorem, vector-valued functions

Suppose $S$ is a piecewise smooth surface which forms the complete boundary of a bounded closed point set $V$ , and $S$ is oriented by its normal being outwards from $V$ . Then

1.6.58 $\iiint _{V}(\nabla\cdot\mathbf{F})dV=\iint _{S}\mathbf{F}\cdot d\mathbf{S},$

Symbols:: $dx$ : differential of $x$ , $S$ : parameterized surface and $V$ : closed region
Permalink:: http://dlmf.nist.gov/1.6.E58
Encodings:: TeX, pMML, png