Digital Library of Mathematical Functions
About the Project
NIST
4 Elementary FunctionsApplications

§4.42 Solution of Triangles

Contents

§4.42(i) Planar Right Triangles

Show Annotations
Notes:
See Hobson (1928, p. 18).
Permalink:
http://dlmf.nist.gov/4.42.i
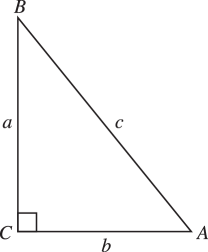
See accompanying text
Figure 4.42.1: Planar right triangle. Magnify
Show Annotations
Symbols:
A: angle, B: angle, C: right angle, a: height, b: base and c: hypotenuse
Permalink:
http://dlmf.nist.gov/4.42.F1
Encodings:
pdf, png
4.42.1\mathop{\sin\/}\nolimits A=\frac{a}{c}=\frac{1}{\mathop{\csc\/}\nolimits A},
Show Annotations
Symbols:
\mathop{\csc\/}\nolimits z: cosecant function, \mathop{\sin\/}\nolimits z: sine function, A: angle, a: height and c: hypotenuse
A&S Ref:
4.3.147
Permalink:
http://dlmf.nist.gov/4.42.E1
Encodings:
TeX, pMML, png
4.42.2\mathop{\cos\/}\nolimits A=\frac{b}{c}=\frac{1}{\mathop{\sec\/}\nolimits A},
Show Annotations
Symbols:
\mathop{\cos\/}\nolimits z: cosine function, \mathop{\sec\/}\nolimits z: secant function, A: angle, b: base and c: hypotenuse
A&S Ref:
4.3.147
Permalink:
http://dlmf.nist.gov/4.42.E2
Encodings:
TeX, pMML, png
4.42.3\mathop{\tan\/}\nolimits A=\frac{a}{b}=\frac{1}{\mathop{\cot\/}\nolimits A}.
Show Annotations
Symbols:
\mathop{\cot\/}\nolimits z: cotangent function, \mathop{\tan\/}\nolimits z: tangent function, A: angle, a: height and b: base
A&S Ref:
4.3.147
Permalink:
http://dlmf.nist.gov/4.42.E3
Encodings:
TeX, pMML, png

§4.42(ii) Planar Triangles

Show Annotations
Notes:
See Hobson (1928, Chapter 10).
Permalink:
http://dlmf.nist.gov/4.42.ii
See accompanying text
Figure 4.42.2: Planar triangle. Magnify
Show Annotations
Symbols:
a: length, b: base, c: length, A: angle, B: angle and C: angle
Permalink:
http://dlmf.nist.gov/4.42.F2
Encodings:
pdf, png
4.42.4\frac{a}{\mathop{\sin\/}\nolimits A}=\frac{b}{\mathop{\sin\/}\nolimits B}=% \frac{c}{\mathop{\sin\/}\nolimits C},
Show Annotations
Symbols:
\mathop{\sin\/}\nolimits z: sine function, a: length, b: base, c: length, A: angle, B: angle and C: angle
A&S Ref:
4.3.148
Permalink:
http://dlmf.nist.gov/4.42.E4
Encodings:
TeX, pMML, png
4.42.5c^{2}=a^{2}+b^{2}-2ab\mathop{\cos\/}\nolimits C,
Show Annotations
Symbols:
\mathop{\cos\/}\nolimits z: cosine function, a: length, b: base, c: length and C: angle
A&S Ref:
4.3.148
Permalink:
http://dlmf.nist.gov/4.42.E5
Encodings:
TeX, pMML, png
4.42.6a=b\mathop{\cos\/}\nolimits C+c\mathop{\cos\/}\nolimits B
Show Annotations
Symbols:
\mathop{\cos\/}\nolimits z: cosine function, a: length, b: base, c: length, B: angle and C: angle
A&S Ref:
4.3.148
Permalink:
http://dlmf.nist.gov/4.42.E6
Encodings:
TeX, pMML, png
4.42.7\hbox{area}=\tfrac{1}{2}bc\mathop{\sin\/}\nolimits A=\left(s(s-a)(s-b)(s-c)% \right)^{{1/2}},
Show Annotations
Symbols:
\mathop{\sin\/}\nolimits z: sine function, a: length, b: base, c: length, s: semi-perimeter and A: angle
A&S Ref:
4.3.148
Permalink:
http://dlmf.nist.gov/4.42.E7
Encodings:
TeX, pMML, png

where s=\tfrac{1}{2}(a+b+c) (the semiperimeter).

§4.42(iii) Spherical Triangles

See accompanying text
Figure 4.42.3: Spherical triangle. Magnify
Show Annotations
Symbols:
A: angle, B: angle, C: angle, a: arc length, b: arc length and c: arc length
Permalink:
http://dlmf.nist.gov/4.42.F3
Encodings:
pdf, png

For these and other formulas see Smart (1962, Chapter 1).

© 2010–2013 NIST / Privacy Policy / Disclaimer / Feedback; Version 1.0.6; Release date 2013-05-06 Math-Image version (See MathML) . A Printed Companionis available.